Lesson 1
Tiling the Plane
Let’s look at tiling patterns and think about area.
Problem 1
Which square—large, medium, or small—covers more of the plane? Explain your reasoning.

Problem 2
Draw three different quadrilaterals, each with an area of 12 square units.

Problem 3
Use copies of the rectangle to show how a rectangle could:
a. tile the plane.
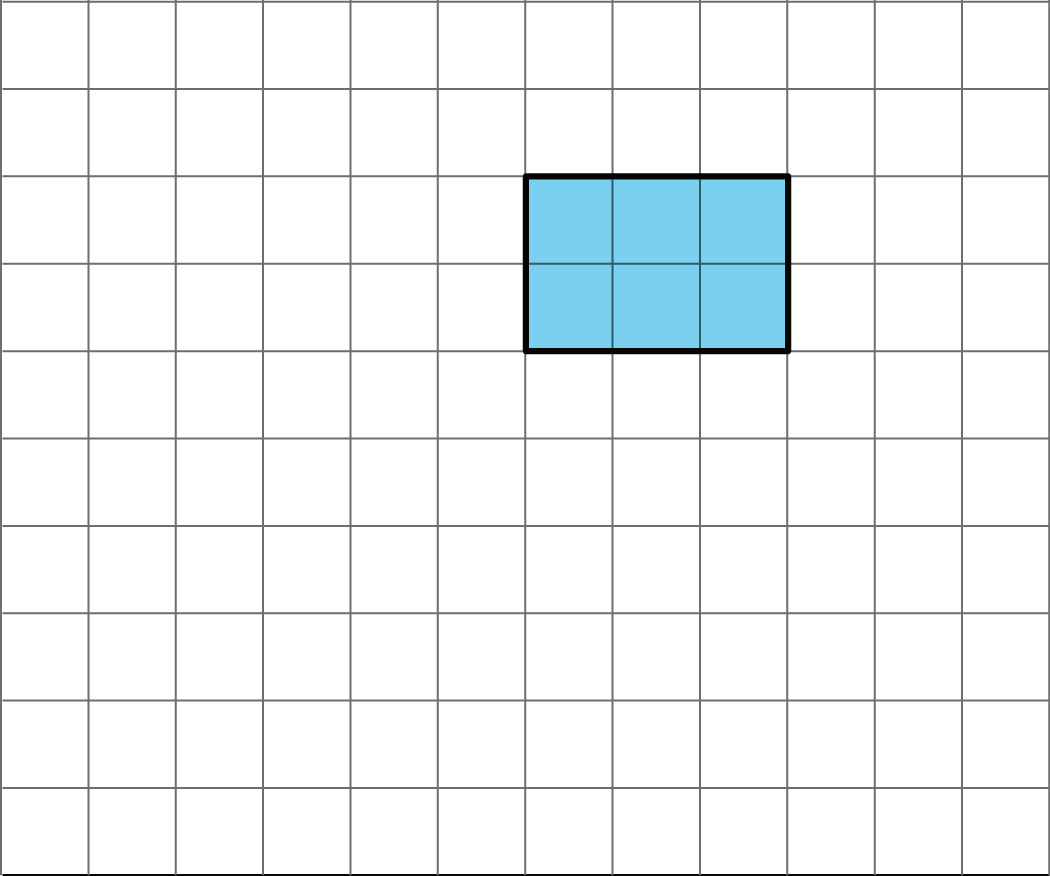
b. not tile the plane.

Problem 4
The area of this shape is 24 square units. Which of these statements is true about the area? Select all that apply.

The area can be found by counting the number of squares that touch the edge of the shape.
It takes 24 grid squares to cover the shape without gaps and overlaps.
The area can be found by multiplying the sides lengths that are 6 units and 4 units.
The area can be found by counting the grid squares inside the shape.
The area can be found by adding \(4 \times 3\) and \(6 \times 2\).
Problem 5
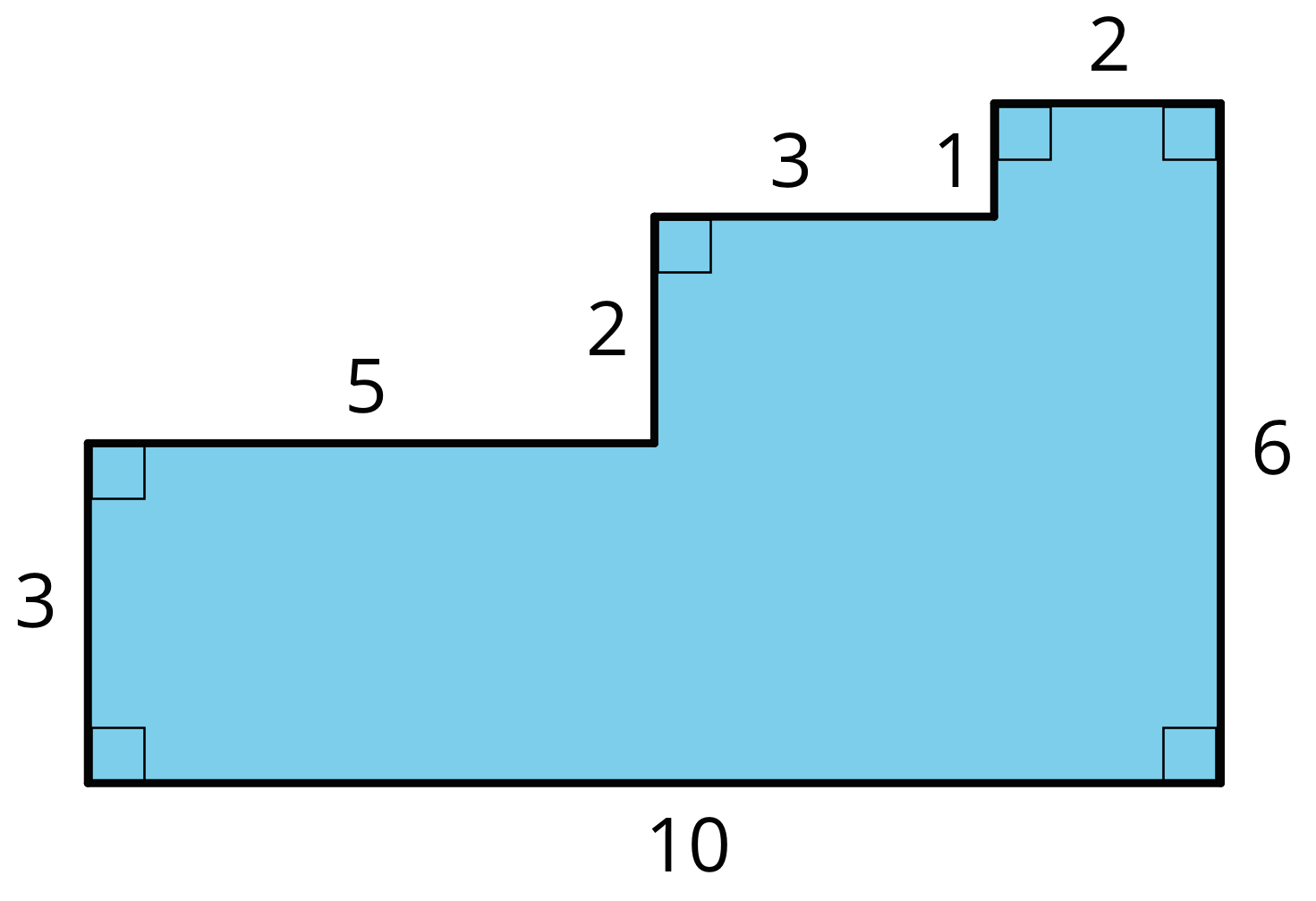
Here are two copies of the same figure. Show two different ways for finding the area of the shaded region. All angles are right angles.

Problem 6
Which shape has a larger area: a rectangle that is 7 inches by \(\frac 34\) inch, or a square with side length of \(2 \frac12\) inches? Show your reasoning.