Lesson 12
Estimate and Add
Warm-up: Number Talk: 99 Hundredths (10 minutes)
Narrative
The purpose of this number talk is for students to develop strategies for adding decimals with a focus on composing a new whole number. Students will work on sums where a new whole number is composed throughout the lesson.
Launch
- Display one expression.
- “Give me a signal when you have an answer and can explain how you got it.”
Activity
- 1 minute: quiet think time
- Record answers and strategy.
- Keep expressions and work displayed.
- Repeat with each expression.
Student Facing
Find the value of each expression mentally.
- \(1.00 + 0.99 + 0.02\)
- \(1.99 + 0.02\)
- \(1.99 + 0.03\)
- \(1.99 + 0.13\)
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
- “How did you use the value of one of the expressions to help you find the value of a different expression?” (I knew that \(1.99 + 0.13\) is 0.1 more than \(1.99 + 0.03\).)
Activity 1: Use the Standard Algorithm to Add Decimals (15 minutes)
Narrative
The purpose of this activity is for students to understand that the standard algorithm for addition can be used with decimals. Students first find the value of a sum of decimals using a strategy that makes sense to them and then see calculations organized using the standard algorithm. They recognize the importance of organizing the calculations and carefully recording any newly composed units.
When students share their explanation of Han's calculations with a partner and revise their work after receiving feedback they critique the reasoning of others and improve their arguments (MP3).
This activity uses MLR1 Stronger and Clearer Each Time. Advances: Conversing
Launch
- Groups of 2
- “Work on the first two problems on your own.”
Activity
- 5–6 minutes: independent work time
MLR1 Stronger and Clearer Each Time
- “Share your description of Han’s work with your partner. Take turns being the speaker and the listener. If you are the speaker, share your ideas and writing so far. If you are the listener, ask questions and give feedback to help your partner improve their work.”
- 3–5 minutes: structured partner discussion.
- Repeat with 2–3 different partners.
- “Revise your initial draft based on the feedback you got from your partners.”
- 2–3 minutes: independent work time
Student Facing
- Find the value of \(5.61 + 2.53\). Explain or show your reasoning.
-
Han used the standard algorithm to add decimals. This is Han’s work. Describe what Han did in each step.
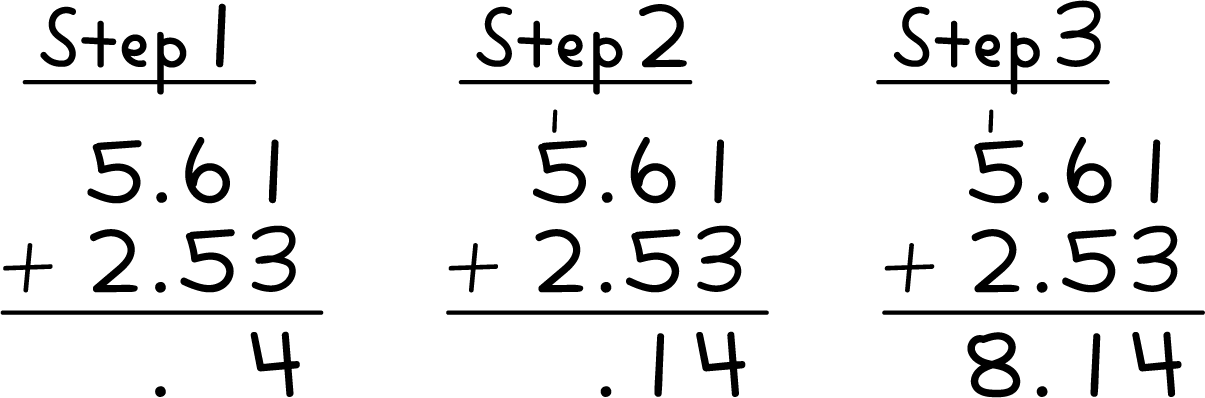
- Use the standard algorithm to find the value of \(6.62+3.74\).
Student Response
For access, consult one of our IM Certified Partners.
Advancing Student Thinking
If students do not get the correct solution, ask, “What 2 whole numbers will the answer be between?”
Activity Synthesis
- “Solve the last problem on your own.”
- 2–3 minutes: independent work time
- “What was helpful about using the standard algorithm?” (It was helpful to line up the numbers and keep track of everything. It was also helpful to add everything in order, step by step.)
- “How was the standard algorithm with decimals the same as for whole numbers?” (I add numbers with the same place value and then when I get a new unit, like the 1 here, I write it over the correct place value.)
Activity 2: Estimate and Find the Value (20 minutes)
Narrative
The purpose of this activity is for students to estimate and then find sums. Students may use the standard algorithm which they just learned to find the sums or they may add by place value. The numbers here are deliberately chosen so that one number has tenths but no hundredths and the other number has hundredths. A new and important feature to adding decimals with the standard algorithm is making sure to add digits with the same place value. In practice, this means that the numbers are not always “right aligned” as they are when adding whole numbers. Students will examine an error in alignment in the next lesson.
Supports accessibility for: Conceptual Processing, Memory
Launch
- Groups of 2
Activity
- 8 minutes: independent work time
- 2 minutes: partner work time
- Monitor for students who use different approaches to add the numbers including using the standard algorithm or place value reasoning.
Student Facing
- Which whole number is the sum \(2.82 + 5.2\) closest to? Explain or show your reasoning.
- What is the value of \(2.82 + 5.2\)? Explain or show your reasoning. Use the standard algorithm if it is helpful.
- Which whole number is the sum \(6.8 + 4.97\) closest to? Explain or show your reasoning.
- What is the value of \(6.8 + 4.97\)? Explain or show your reasoning. Use the standard algorithm if it is helpful.
Student Response
For access, consult one of our IM Certified Partners.
Advancing Student Thinking
If students don’t have a strategy for determining which whole number the sum is closest to, ask, “Will the sum be greater or less than 8?”
Activity Synthesis
- Invite students who used different strategies to add to share their work for the first problem.
- “What is the same about their strategies? What is different?” (In both of them, they had to make sure to add the same place values. They also both composed a new unit. One added on in parts, by place value, and the other used the standard algorithm.)
- “How did the estimate help you with your calculation?” (I saw that 4.97 was really close to 5 and that gave me the idea of adding 5 which I could do mentally and then taking away 0.03.)
Lesson Synthesis
Lesson Synthesis
“Today we added decimals and we used the standard algorithm.”
Refer to the poster from the previous lesson.
“Did we answer any of the questions that we wondered about?”
Add to or change poster as necessary.
“How is using the standard algorithm for adding decimals the same as and different from the standard algorithm for adding whole numbers?” (The calculations are organized vertically with newly composed units recorded above the numbers. I make sure to add digits with the same place value. I need to keep track of where the decimal is in each number.)
Cool-down: Sums of Decimals (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
