Lesson 23
Divide Whole Numbers by Decimals
Warm-up: True or False: Tenths and Hundredths (10 minutes)
Narrative
The purpose of this warm-up is for students to analyze statements about quotients of whole numbers by 0.1 or 0.01. Students compare the value of quotients by 0.1 and 0.01. They can analyze the statements either by calculating the value of the expressions or reasoning about the relationship between 0.1 and 0.01, namely that there are ten hundredths in a tenth.
Launch
- Display one statement.
- “Give me a signal when you know whether the statement is true and can explain how you know.”
- 1 minute: quiet think time
Activity
- Share and record answers and strategy.
- Repeat with each statement.
Student Facing
Decide if each statement is true or false. Be prepared to explain your reasoning.
- \(6 \div 0.01 = 60\)
- \(6 \div 0.1 < 6 \div 0.01\)
- \(6 \div 0.01 = 60 \div 0.1\)
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
- Display second statement.
-
“How can you prove this statement is true without finding the value of the expressions on both sides of the equal sign?” (I can think about the size of the quotients. They both show 6 being divided into groups, but the size of the groups is bigger in \(6\div0.1\) so there will be fewer groups.)
Activity 1: Same Divisor, Different Dividend (15 minutes)
Narrative
The purpose of this activity is for students to find quotients of a whole number by tenths or hundredths. This activity focuses on divisors of 0.2 and 0.02 to build on students' previous work dividing by 0.1 and 0.01. The strategies, diagrams and place value reasoning used in the previous lessons still apply. Students may also think about the problems using multiplication. For example \(1 \div 0.2 = 5\) because \(5 \times 0.2 = 1\).
Required Materials
Materials to Copy
- Small Grids
Launch
- Groups of 2
- Give students access to blackline masters with grids.
Activity
- 1–2 minutes: quiet think time
- 8–10 minutes: partner work time
- Monitor for students who represent their reasoning with:
- diagrams
- expressions or words using multiplication
Student Facing
-
Find the value of each expression. Explain or show your reasoning.
- \(1 \div 0.2\)
- \(2 \div 0.2\)
- \(3 \div 0.2\)
- \(4 \div 0.2\)
-
Find the value of each expression. Explain or show your reasoning.
- \(1 \div 0.02\)
- \(2 \div 0.02\)
- \(3 \div 0.02\)
- \(4 \div 0.02\)
- What patterns do you notice?
Student Response
For access, consult one of our IM Certified Partners.
Advancing Student Thinking
Activity Synthesis
- Ask selected students to share the representations listed above.
- “How are the representations the same? How are they different?” (They both figured out how many tenths or hundredths are in one whole. Then they multiplied that by the number of wholes. One of them used a picture and one of them reasoned about the size of tenths and hundredths to find how many 0.2's and 0.02's are in one whole.)
- Display a student's completed work showing the values of the quotients.
- “What patterns do you see across the sets of equations?” (The quotients with a divisor of 0.01 are 10 times larger than those with a divisor of 0.1. The quotients with a divisor of 0.1 are a tenth of the value of those with a divisor of 0.01.)
- Record the patterns as students describe them.
Activity 2: Evaluate Expressions (20 minutes)
Narrative
The purpose of this activity is for students to find the value of quotients where the divisor is less than 1 and where the dividend is large enough that drawing a complete diagram is cumbersome. Instead, students are encouraged to use a diagram to find how many divisor sized groups are in 1 whole and then multiply the dividend by that number to find the value of the quotient. When students use the value of \(1 \div 0.2\) and multiplication to find the value of \(12 \div 0.2\) they are using regularity in reasoning (MP8).
This activity uses MLR1 Stronger and Clearer Each Time. Advances: Conversing.
Supports accessibility for: Conceptual Processing, Memory
Required Materials
Materials to Copy
- Small Grids
Launch
- Groups of 2
-
Give students access to blackline masters with hundredths grids.
Activity
- 3–5 minutes: independent work time
- Monitor for students who use the following strategies for problem 1:
- reason about how many divisor-sized groups are in 1 whole, possibly with a diagram, and then multiply by the dividend
- use multiplication equations to find the value of the division expressions
Student Facing
- Find the value of the expression. Use a diagram if it is helpful.
\(12 \div 0.2\)
- This is the diagram and explanation Tyler used to justify why \(12 \div 0.2 = 60\).
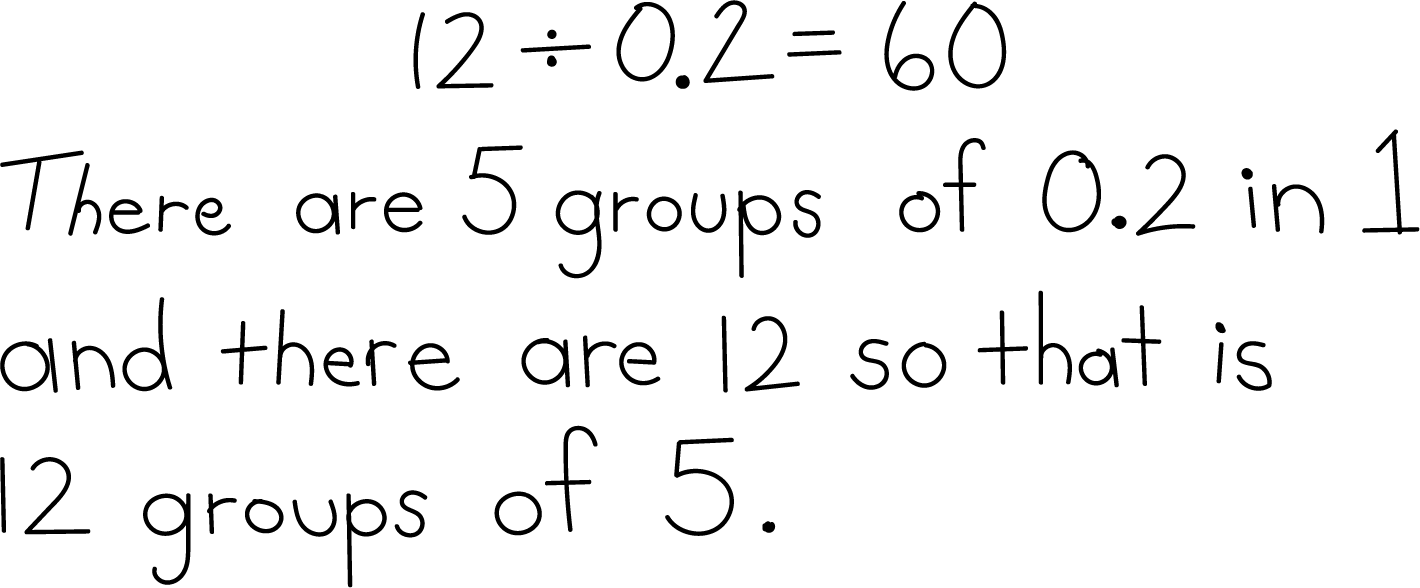
Explain how the expression \(12 \times (1 \div 0.2)\) relates to Tyler's reasoning.
-
Find the value of each expression.
- \(14 \div 0.5\)
- \(5 \div 0.25\)
Student Response
For access, consult one of our IM Certified Partners.
Advancing Student Thinking
Activity Synthesis
- Ask previously identified students to share their solutions and strategies for evaluating the expression in the first problem.
- “How was multiplication useful to find the value of the expression in the first problem?” (I didn't have to draw 12 wholes because I knew there were five 0.2s in each one so that would be \(12 \times 5\) total.)
- “Share your response to problem 2 with your partner. Take turns being the speaker and the listener. If you are the speaker, share your ideas and writing so far. If you are the listener, ask questions and give feedback to help your partner improve their work.”
- 3-5 minutes: structured partner discussion
- Repeat with 2 different partners.
- “Revise your initial draft based on the feedback you got from your partners.”
- 2-3 minutes: independent work time
Lesson Synthesis
Lesson Synthesis
“Today we divided whole numbers by decimals.”
Display two expressions:
\(2 \div 0.2\)
\(2 \div 0.5\)
“In both these cases, 2 is being divided by a decimal number. Describe to your partner how you would find the value of each expression.” (I would use the 2 grids and divide them into groups of 0.2 or 0.5 and then see how many of them there are.)
Display:
\(18 \div 0.2\)
\(18 \div 0.5\)
“How does your strategy for the first two expressions change with this set of problems? Why?” (For these, the hundredths grids still help to visualize the 0.2s and 0.5s in one whole, but I don't want to draw 18 of them so I would just multiply the 0.2s in 1 whole or the 0.5s in one whole by 18.)
Cool-down: Divide Whole Numbers by Decimals (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.

