Lesson 15
Estimate and Subtract
Warm-up: Number Talk: One and Five Tenths (10 minutes)
Narrative
The purpose of this number talk is for students to develop mental strategies for subtracting decimals where decomposition of one or more units is needed when subtracting by place value. These strategies will be useful as students subtract more complex decimals and need to pay close attention to place value.
Launch
- Display one expression.
- “Give me a signal when you have an answer and can explain how you got it.”
- 1 minute: quiet think time
Activity
- Record answers and strategy.
- Keep expressions and work displayed.
- Repeat with each expression.
Student Facing
Find the value of each expression mentally.
- \(1.50 - 0.51\)
- \(1.50 - 0.52\)
- \(1.50 - 0.60\)
- \(1.50 - 0.62\)
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
- “How did you use the value of the third expression to find the value of the last expression?” (I know 0.62 is two hundredths more than 0.60 so I subtracted 2 hundredths from 0.90 and that left 0.88.)
Activity 1: Revisit the Algorithm (15 minutes)
Narrative
The purpose of this activity is for students to understand that the standard algorithm for subtraction can be used with decimals. Students first find the value of a difference of decimals using a strategy that makes sense to them and then see calculations organized using the standard algorithm. When students calculate using a strategy of their choice, they may or may not show decomposition of a whole into 10 tenths. The standard algorithm explicitly shows this decomposition.
When students share their explanation of Han's calculations with a partner and revise their work after receiving feedback they critique the reasoning of others and improve their arguments (MP3).
This activity uses MLR1 Stronger and Clearer Each Time. Advances: Conversing.
Launch
- Groups of 2
- “Work on the first two problems on your own.”
Activity
- 5–6 minutes: independent work time
- “Share your description of Han’s work with your partner. Take turns being the speaker and the listener. If you are the speaker, share your ideas and writing so far. If you are the listener, ask questions and give feedback to help your partner improve their work.”
- 3–5 minutes: structured partner discussion
- Repeat with 2–3 different partners.
- “Revise your initial draft based on the feedback you got from your partners.”
- 2–3 minutes: independent work time
Student Facing
- Find the value of \(8.53 - 2.7\). Show your reasoning.
- Han used the standard algorithm to subtract decimals. This is Han’s work. Describe what Han did in each step.
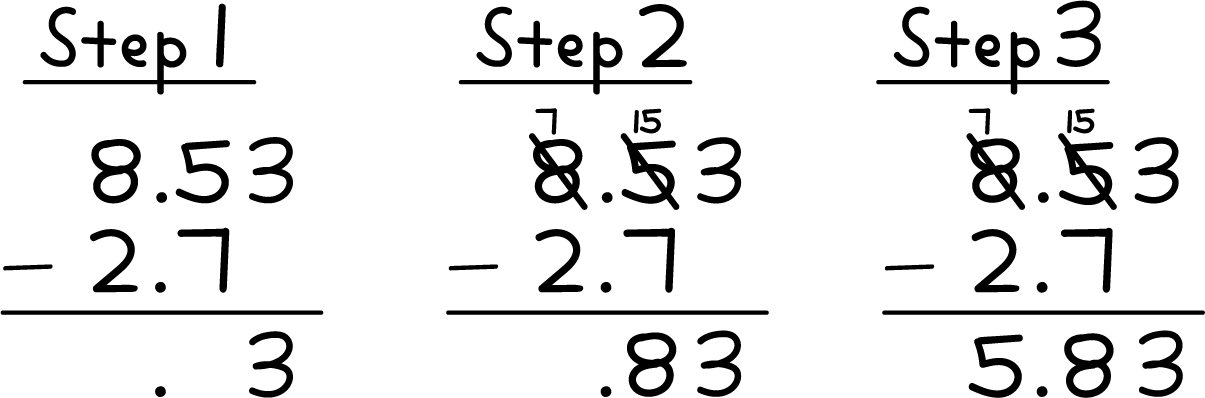
- Use the standard algorithm to find the value of \(6.62 - 3.71\).
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
- “Solve the last problem on your own.”
- 2-3 minutes: independent work time
- “How is the standard algorithm for subtraction the same as the standard algorithm for addition?” (I work from right to left. I line up all of the place values and make sure the digits I am subtracting have the same place value.)
- “How is the standard algorithm for subtraction different than the standard algorithm for addition?” (Sometimes I need to decompose a unit. I need to decompose a whole into 10 tenths. With addition, I sometimes need to compose a new unit.)
Activity 2: Estimate and Subtract (20 minutes)
Narrative
The purpose of this activity is for students to estimate and then find differences. Students just learned the standard algorithm for subtraction can be used with decimals in the previous activity and may use it here. All students should be encouraged to find the differences in a way that makes sense to them. Any subtraction strategy they use will require close attention to place value and this is the focus of the synthesis.
Supports accessibility for: Conceptual Processing, Visual-Spatial Processing
Launch
- Groups of 2
Activity
- 8 minutes: independent work time
- 2 minutes: partner work time
- Monitor for students who:
- use place value understanding to subtract by place
- use the standard algorithm
- use a compensation strategy to subtract 9.8
Student Facing
- Which whole number is the difference \(15.27 - 4.3\) closest to? Explain or show your reasoning.
- What is the value of \(15.27 - 4.3\)? Explain or show your reasoning.
- Which whole number is the difference \(16.14 - 9.8\) closest to? Explain or show your reasoning.
- What is the value of \(16.14-9.8\)? Explain or show your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
- Invite students to share their strategies for finding the difference \(15.27 - 4.3\).
- “How are the strategies the same? How are they different?” (They both broke up 4.3 into pieces and then subtracted each piece. Some students used the standard algorithm and some subtracted by place value. The standard algorithm works in one way. There are different ways to subtract 4.3 working by place value.)
- Invite students to share their estimate for \(16.14 - 9.8\).
- “How did you know that the value would be close to 6?” (16.14 is just a little more than 16 and 9.8 is almost 10 so I used whole number subtraction to estimate, \(16 - 10 = 6\).)
- “Did the estimate help you with the calculation?” (Yes, I used the standard algorithm and got an answer that was just a little more than 6 and that agreed with my estimate. Yes, the estimate made me think of subtracting 10 which I could do in my head and then adding back 0.2 which I could also do in my head.)
Activity 3: Compare Calculations to Evaluate a Difference [OPTIONAL] (10 minutes)
Narrative
The purpose of this activity is for students to analyze a common error when using the standard algorithm to subtract decimals. This activity is recommended if students need additional practice with the standard algorithm when the two numbers do not have the same number of decimal places. The standard addition algorithm requires students to subtract digits with the same place value. In the given example the two numbers are “right aligned” as when subtracting whole numbers and this leads to the error of subtracting hundredths from tenths, tenths from ones, and so on as if these digits had the same place value.
When students identify and correct Elena's error they construct viable arguments and critique the reasoning of others (MP3).
This activity uses MLR3 Clarify, Critique, and Correct. Advances: Reading, Writing, Representing.
Launch
- Groups of 2
Activity
- 1–2 minutes: quiet think time
- 6–8 minutes: partner work time
- Display Elena’s solution and explanation.
- Read the explanation aloud.
- “What do you think Elena means? Is anything unclear?” (She says the answer will be less than 622.3, but she doesn’t say how much less. The answer will be a lot less than 615.21.)
- “With your partner, work together to write a revised solution and explanation.”
- (Optional) Display and review the following criteria:
- Explanation of mistakes
- Specific words and phrases
- Decimal point
- Place value
- Labeled diagram
- Correct solution
- 3–5 minutes: partner work time
- Select 1–2 groups to share their revised explanation with the class.
- “What is the same and different about the revised solutions and explanations?”
Student Facing
- Find the value of \(622.35 - 71.4\). Explain or show your reasoning.
- Elena and Andre found the value of \(622.35 - 71.4\). Who do you agree with? Explain or show your reasoning.
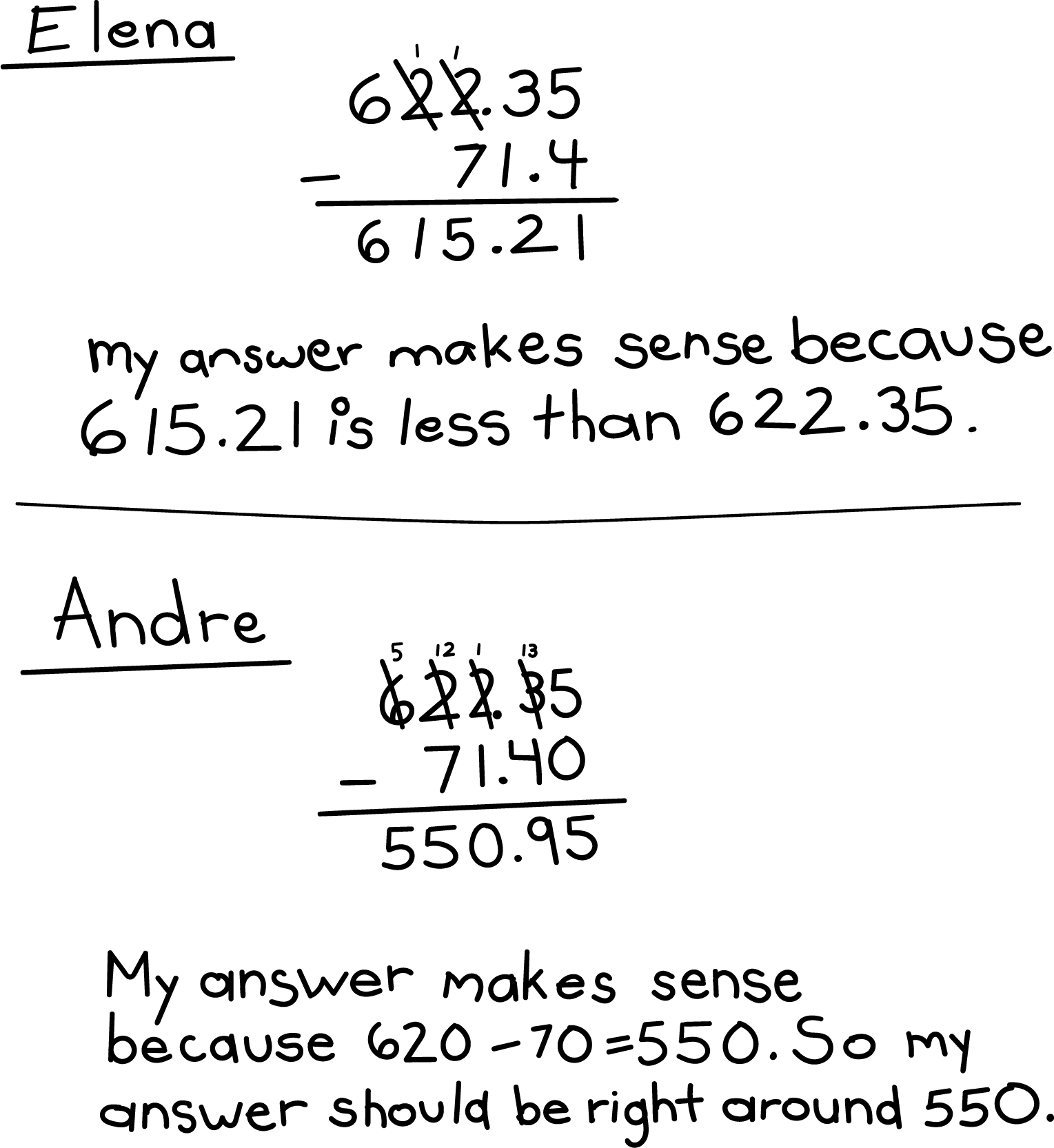
Student Response
For access, consult one of our IM Certified Partners.
Advancing Student Thinking
Activity Synthesis
- Display Andre’s solution and explanation.
- “Why do you think Andre wrote 71.40 instead of 72.4?” (It helps him keep the place values and decimals in line so he doesn’t mix up the places when he is subtracting. 71.40 is equivalent to 71.4.)
- Display Elena’s solution.
- “How can you see without finding the difference that Elena’s answer is not correct?” (Taking 71 away from 622 is a lot less than 615. \(620-70=550\) so the answer should be around 550.)
Lesson Synthesis
Lesson Synthesis
“Today we subtracted decimals and we used the standard algorithm.”
“How is the standard algorithm for subtracting the same and different when you subtract whole numbers or decimals?” (When I can’t subtract in one place, I need to move to a larger place and break up a larger unit. I have to keep track of the decimal points and make sure that I am subtracting the same place values.)
“Are there other subtraction strategies that you use for whole numbers that also work with decimals?” (Yes. I can use addition. I can add on to the smaller number. I can also subtract by place value or use compensation.)
Cool-down: Subtract Decimals (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.