Lesson 15
Reasoning About Angles (Part 2)
Warm-up: How Many Do You See: Obtuse Angles (10 minutes)
Narrative
Launch
- Groups of 2
- “How many angles do you see? How do you see them?”
- Display the image.
- 1 minute: quiet think time
Activity
- Display the image.
- “Discuss your thinking with your partner.”
- 1 minute: partner discussion
- Record responses.
Student Facing
How many angles do you see in the folded paper heart?

Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
- “How did you make sure all the angles are accounted for?”(I put a mark through them or numbered them.)
- “How many obtuse angles are in this image?” (10)
- Label each obtuse angle with reasoning from students.
- Consider asking:
- “Who can restate in different words the way _____ saw the angles?”
- “Did anyone see the angles the same way but would explain it differently?”
- “Does anyone want to add an observation to the way _____ saw the angles?”
Activity 1: Shaded and Unshaded Angles (15 minutes)
Narrative
Previously, students found numerous angle sizes by reasoning and without using a protractor. They have done so with problems with and without context. In this activity, students consolidate various skills and understandings gained in the unit and apply them to solve problems that are more abstract and complex. They rely, in particular, on their knowledge of right angles and straight angles to reason about unknown measurements. (Students may need a reminder that an angle marked with a small square is a right angle.)
The angles with unknown measurements are shaded but not labeled, motivating students to consider representing them (or their values) with symbols or letters for easier reference. Students may also choose to write equations to show how they are thinking about the problems.
When students use the fact that angles making a line add up to \(180^\circ\) and that angles making a right angle add up to \(90^\circ\) they make use of structure to find the unknown angle measures (MP7).
Advances: Conversing, Representing
Supports accessibility for: Conceptual Processing, Memory, Attention
Launch
- Groups of 2
Activity
- 5 minutes: independent work time
- 2 minutes: partner discussion
- Monitor for students who:
- use symbols or letters to represent unknown angles
- write equations to help them reason about the angle measurements
Student Facing
Find the measurement of each shaded angle. Show how you know.

Student Response
For access, consult one of our IM Certified Partners.
Advancing Student Thinking
Activity Synthesis
- Display the angles. Select students to share their responses. Record and display their reasoning.
- Highlight equations that illuminate the relationship between the known angle, the unknown angle, and the reference angle (\(90^\circ\), \(180^\circ\), or \(360^\circ\)). For instance: \(62 + p = 90\), \(71 + r + 90 = 180\), \(x + 154 = 180\), and so on.
- Label the diagrams with letters or symbols as needed to facilitate equation writing.
- When discussing the last question, highlight that finding unknown values sometimes involve multiple steps, and some steps may need to happen before others.
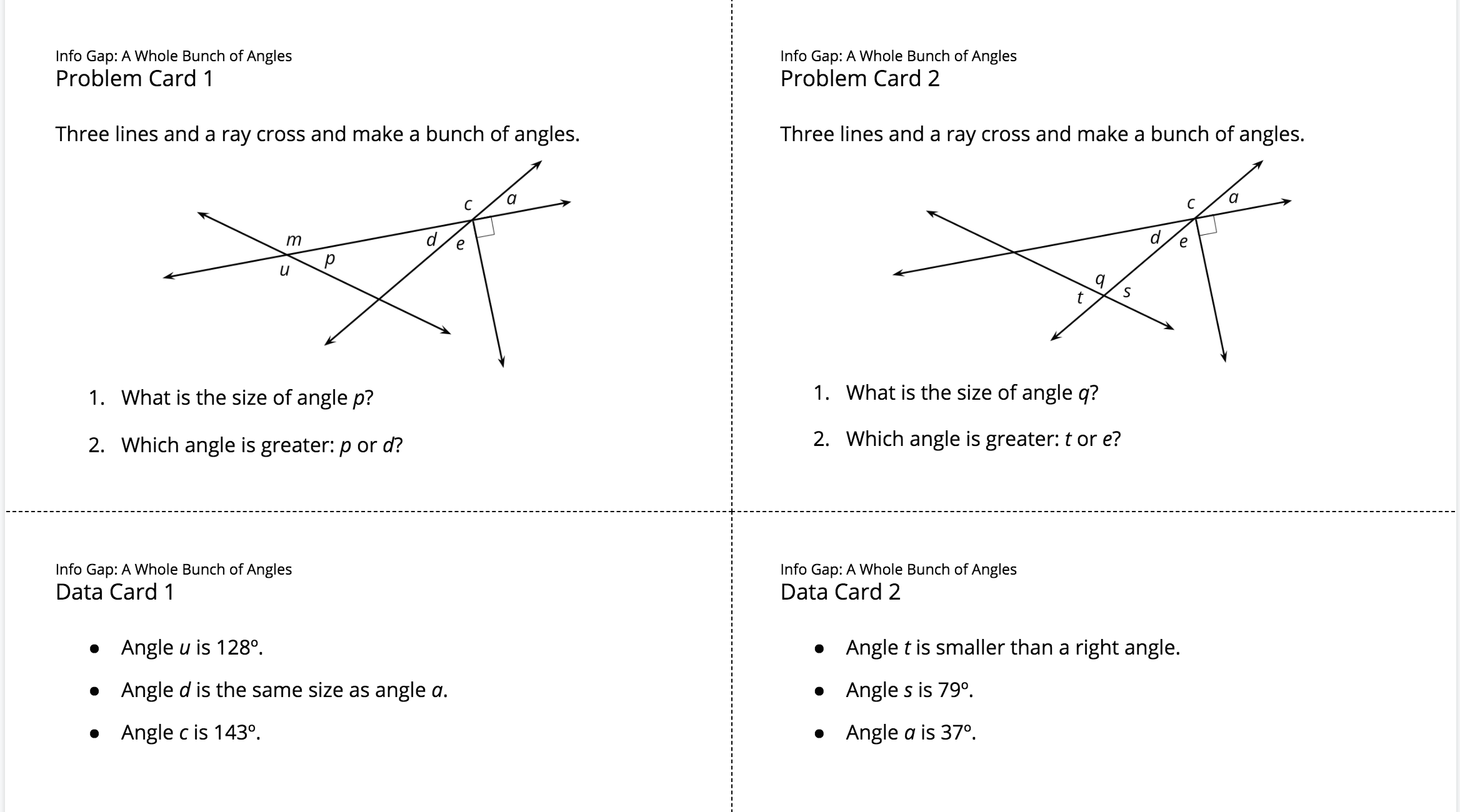
Activity 2: Info Gap: A Whole Bunch of Angles (20 minutes)
Narrative
In this Info Gap activity, students solve abstract multi-step problems involving an arrangement of angles with several unknown measurements. By now students have the knowledge and skills to find each unknown value, but the complexity of the diagram and the Info Gap structure demand that students carefully make sense of the visual information and look for entry points for solving the problems. They need to determine what information is necessary, ask for it, and persevere if their initial requests do not yield the information they need (MP1). The process also prompts them to refine the language they use and ask increasingly more precise questions until they get useful input (MP6).
Here is an image of the cards for reference:
Required Materials
Materials to Copy
- Info Gap: Whole Bunch of Angles
Required Preparation
- Create a set of cards from the blackline master for each group of 2.
Launch
- Groups of 2
MLR4 Information Gap
- Display the task statement, which shows a diagram of the Info Gap structure.
- 1–2 minutes: quiet think time
- Read the steps of the routine aloud.
- “I will give you either a problem card or a data card. Silently read your card. Do not read or show your card to your partner.”
- Distribute the cards.
- “The diagram is not drawn accurately, so using a protractor to measure is not recommended.”
- 1–2 minutes: quiet think time
- Remind students that after the person with the problem card asks for a piece of information, the person with the data card should respond with “Why do you need to know (restate the information requested)?”
Activity
- 5 minutes: partner work time
- After students solve the first problem, distribute the next set of cards. Students switch roles and repeat the process with Problem Card 2 and Data Card 2.
Student Facing
Your teacher will give you either a problem card or a data card. Do not show or read your card to your partner.

Pause here so your teacher can review your work. Ask your teacher for a new set of cards and repeat the activity, trading roles with your partner.
Student Response
For access, consult one of our IM Certified Partners.
Advancing Student Thinking
Activity Synthesis
- Select students to share how they found each angle measure. Record their reasoning and highlight equations that clearly show the relationships between angles.
- “Which angle measurements were easy to find? What made them easy?” (Sample response: \(p\) and \(d\), because it was fairly easy to see that each of them and a neighboring angle make a straight angle.)
- “Which ones were a bit more involved? Why?” (Sample response: \(e\), because there are 5 angles that meet at that point. We needed to find \(a\) or \(d\) before finding \(e\).)
Lesson Synthesis
Lesson Synthesis
“Today we solved angle problems involving multiple steps, all without measuring with a protractor.”
Display the two diagrams on the problem cards of the Info Gap activity. Label the angles whose measurements are given on the data cards. (\(128^\circ\) for \(u\), \(143^\circ\) for \(c\), \(79^\circ\) for \(s\), and \(37^\circ\) for \(a\).)


Focus the discussion on how equations could be used to represent students’ reasoning process and to help find the unknown angle measurements.
“What equations can we write to help us find the value of \(p\)? What about \(d\)?” (See sample equations in student responses.)
Cool-down: Heart to Heart (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Section Summary
Student Facing
Earlier in the unit, we learned that a right angle measures exactly \(90^\circ\). In this section, we learned other ways to name angles based on their measurements.
-
Acute angles are less than 90º.

-
Obtuse angles are greater than 90º but less than 180º.

-
Straight angles are exactly 180º.

We also solved problems about angles. For example, if two angles make a right angle or a straight angle, we can use the size of one angle to find the other.
The shaded angle here must be \(28^\circ\) because it makes a right angle when combined with the \(62^\circ\) angle.

Another example: Knowing that a full turn measures \(360^\circ\), we reasoned that the long hand of a clock makes:
- a \(360^\circ\) angle every hour
- a \(180^\circ\) angle every one-half hour
- a \(90^\circ\) angle every 15 minutes
- a \(60^\circ\) angle every 10 minutes
