Lesson 15
The Nearest Multiples of 1,000, 10,000, and 100,000
Warm-up: Estimation Exploration: What Could It Be? (10 minutes)
Narrative
The purpose of an Estimation Exploration is to practice the skill of estimating a reasonable answer based on experience and known information. In this case, students rely on their familiarity with number lines and their understanding of numbers within 1,000 to estimate the value represented by a point on a number line. The reasoning here prepares students to think about the halfway point between two benchmark values as a way to estimate numbers.
Launch
- Groups of 2
- Display image.
- “What is an estimate that’s too high? Too low? About right?”
- 1 minute: quiet think time
Activity
- “Discuss your thinking with your partner.”
- 1 minute: partner discussion
- Record responses.
Student Facing
What number could this point represent?

Record an estimate that is:
| too low | about right | too high |
|---|---|---|
| \(\phantom{\hspace{2.5cm} \\ \hspace{2.5cm}}\) | \(\phantom{\hspace{2.5cm} \\ \hspace{2.5cm}}\) | \(\phantom{\hspace{2.5cm} \\ \hspace{2.5cm}}\) |
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
- Consider asking: “Is anyone’s estimate less than 500? Is anyone’s estimate greater than 800?”
- “How did you go about making an estimate when only 0 and 1,000 are shown on the line?”
- If no students mentioned using the halfway point or 500 as a reference, ask them about it.
- “How did the midpoint for 500 help you make an estimate?”
- Consider asking: “Did anyone partition the space between 500 to 1,000 into smaller spaces? How did that help you estimate?”
Activity 1: Closer to This or That? (20 minutes)
Narrative
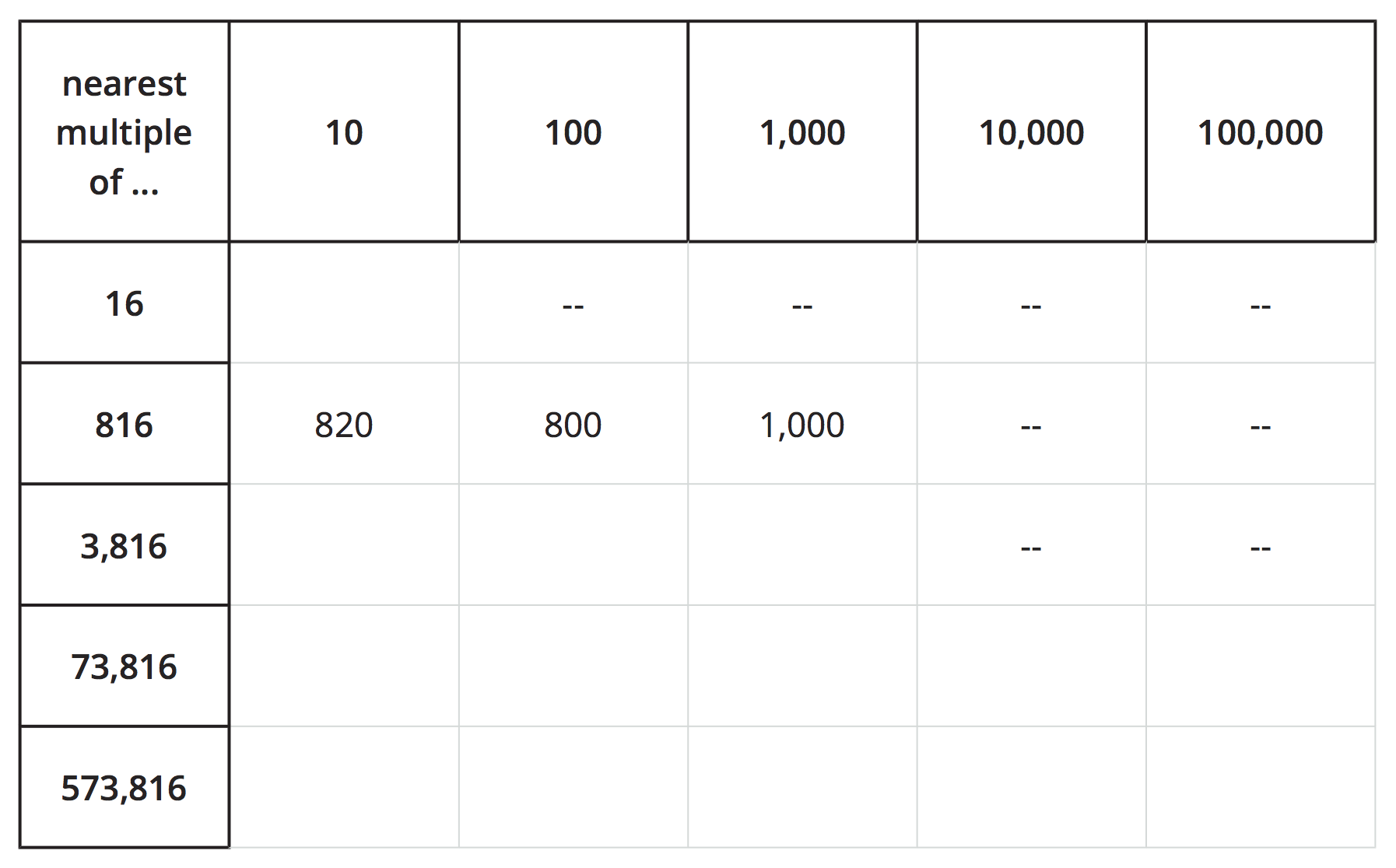
This activity transitions students from reasoning visually to reasoning numerically about the nearest multiples of 1,000, 10,000, and 100,000. Students identify the nearest multiples of 10, 100, 1,000, 10,000 and 100,000 for a series of related numbers—16, 816, 3,816, 73,816, and 573,816—and use number lines to support their thinking as needed. Tables are used to highlight the idea that a given number can be closest to a smaller number or a greater number depending on the place attended to. For example, for 816, the nearest multiple of 10 is 820 and the nearest multiple of 100 is 800.
For students, rounding to the unit in the leftmost place is not usually an issue, but rounding to the unit represented by a place in the middle of a number often is, as the nearby digits can be distracting. (For example, rounding 573,816 to the nearest 1,000 is more difficult than rounding to the nearest 100,000.) This activity allows students to work with a set of related numbers that grows by an additional digit each time, and gives them a way to think of a large number as composed of smaller place-value parts, each of which they can manage to round.
Supports accessibility for: Conceptual Processing, Language, Memory
Launch
- Groups of 2
Activity
- “Work on the activity independently for a few minutes. Then, share your responses with your partner.”
- 6–7 minutes: independent work time
- 3–4 minutes: partner discussion
Student Facing
-
Answer each question. Use the number lines if they are helpful.
- Is 16 closer to 10 or to 20?
- Is 816 closer to 800 or to 900?
- Is 3,816 closer to 3,000 or 4,000?
- Is 73,816 closer to 70,000 or 80,000?
- Is 573,816 closer to 500,000 or 600,000?
- Is 16 closer to 10 or to 20?
-
For 816:
- The nearest multiple of 1,000 is 1,000.
- The nearest multiple of 100 is 800.
- The nearest multiple of 10 is 820.
Complete the table with the nearest multiple of 10, 100, 1,000, 10,000, and 100,000 for each number.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
- Display the blank table from the activity. Invite students to share their responses to complete the table. Discuss any disagreements.
- “How might we tell the nearest multiple of 1,000 for 573,816 without using a number line?” (Sample responses:
- Find two multiples of 1,000 that are closest to the number, one that is greater and one that is less. For 573,816, they are 573,000 and 574,000. If the number is less than their midpoint, 573,500, then it is closer to the lower multiple of 1,000. If it is more than 573,500, then it is closer to the higher one.
- Look at the value of the digits to the right of the thousands—the hundreds, tens, and ones. If it is less than 500, then it is closer to the lower multiple of 1,000. If it is more than 500, then it is closer to the higher multiple of 1,000.)
Activity 2: Closer to Which Number? [OPTIONAL] (10 minutes)
Narrative
Launch
- Groups of 2
Activity
- “Work independently for a few minutes. Then, discuss your responses with your partner.”
- 5 minutes: independent work time
- 2 minutes: partner discussion
Student Facing
-
Answer each question. Label and use the number lines if they are helpful.
- Is 425,193 closer to 400,000 or 500,000?
- Is 425,193 closer to 420,000 or 430,000?
- Is 425,193 closer to 425,000 or 426,000?
- Is 425,193 closer to 425,100 or to 425,200?
- Is 425,193 closer to 425,190 or to 425,200?
- Is 425,193 closer to 400,000 or 500,000?
-
For the number 425,193:
-
The nearest multiple of 100,000 is _______________.
-
The nearest multiple of 10,000 is _______________.
-
The nearest multiple of 1,000 is _______________.
-
The nearest multiple of 100 is _______________.
-
The nearest multiple of 10 is _______________.
-
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
- Invite students to share their responses and reasoning.
- “Which nearest multiples were you able to identify fairly easily?”
- “Which were a bit more challenging, if any? Why might that be?”
Activity 3: What’s the Nearest Multiple? (15 minutes)
Narrative
In this activity, students encounter numbers that are exactly between two consecutive multiples and thus are closer to neither multiple (or have two nearest multiples). This offers students an opportunity to construct different viable arguments, support them, and critique the reasoning of others (MP3).
Some students may bring up the convention of rounding up that they learned in grade 3, but if not, it is not necessary to remind them during the activity synthesis. This convention is discussed in a later lesson. It is acceptable at this point for students to say that there are two nearest multiples of 100 or that there are none.
Advances: Speaking
Launch
- Groups of 2
- Give students access to blank number lines.
Activity
- “Work with your partner on the first problem. Pause before continuing to the second set.”
- 4–5 minutes: group work time on the first set of problems
- Pause for a whole-class discussion.
- Invite students to share their responses for part b. Discuss how 136,850 is different from other numbers they’ve seen so far and what students think the nearest multiple of 100 is.
- “Let’s find the nearest multiples for some other numbers and see if we come across other cases where there is not a single nearest multiple.”
- “Take a few quiet minutes to work on the last problem.”
- 3–5 minutes: quiet work time
Student Facing
-
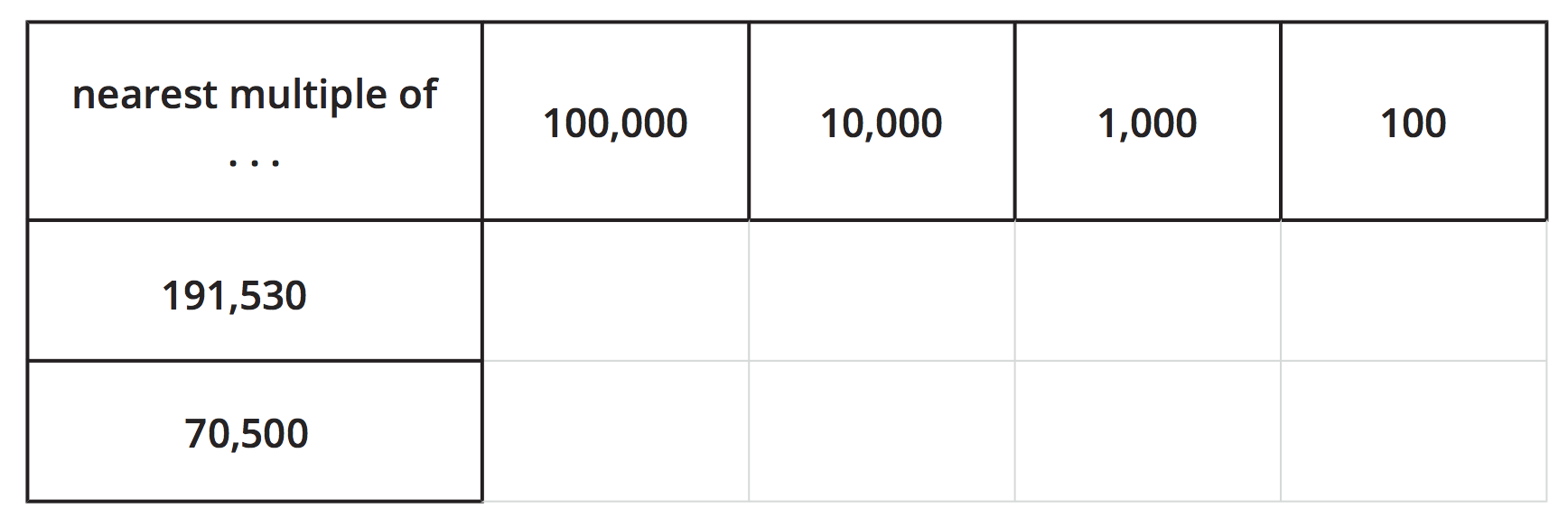
For the number 136,850, Han can name the nearest multiple of 100,000, 10,000, and 1,000.
He is stuck when trying to name the nearest multiple of 100.


- In the table, write the nearest multiples that Han knows for each place value. Use number lines if they are helpful.
- Why might it be tricky to name the nearest multiple of 100 for 136,850? What do you think it is?
- Name the nearest multiples of 100,000, 10,000, 1,000, and 100 for each number.
Student Response
For access, consult one of our IM Certified Partners.
Advancing Student Thinking
Activity Synthesis
- “Were there times when you couldn’t identify one nearest multiple? When?” (When finding the nearest multiple of 1,000 for 70,500.) “Why was there not one nearest multiple?” (70,500 is exactly halfway between 70,000 and 71,000.)
- “We see 5 in the hundreds place for 191,530. Does this number also have no single nearest multiple of 1,000?” (It does have one, 192,000. The 30 makes it greater than the halfway point between 191,000 and 192,000.)
Lesson Synthesis
Lesson Synthesis
“Today we learned to find the nearest multiple of 1,000, 10,000, and 100,000 for some large numbers. Let’s revisit the strategies we used.”
“How would you go about finding the nearest multiple of 100,000 for a number like 318,495?” Consider providing some sentence frames: “First, I would. . . Next, I would . . . Then, I would . . .”
“What about the nearest multiples of 10,000 and 1,000?”
“Does the number 318,500 have the same nearest multiples of 1,000, 10,000, and 100,000 as 318,495? Why or why not?” (It has the same nearest multiples of 100,000 and 10,000, but not the same nearest multiple of 1,000. The nearest multiple of 1,000 for 318,495 is 318,000, but for 318,500, there are two multiple of 1,000 that are the same distance away: 318,000 and 319,000.)
Cool-down: The Nearest Multiples (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.





