Lesson 1
Decimal Numbers
Warm-up: Notice and Wonder: Shaded Grid (10 minutes)
Narrative
Launch
- Groups of 2
- Display the image.
- “What do you notice? What do you wonder?”
- 1 minute: quiet think time
Activity
- “Discuss your thinking with your partner.”
- 1 minute: partner discussion
- Share and record responses.
Student Facing

Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
- “If the large square represents 1, what fraction of it is shaded? What fraction is not shaded? How do you know?” (\(\frac{6}{100}\) are shaded. There are 100 small squares, and 6 of them shaded and 94 are not.)
Activity 1: Shady Fractions (20 minutes)
Narrative
In this activity, students use a square grid of 100 to revisit the meaning of tenths and hundredths and to make sense of the decimal notation for these fractions. They begin to make connections between the familiar representations of a fraction—using a diagram, fraction notation, and words—and the newly introduced decimal notation, and to notice similarities in their structure (MP2, MP7). It is important for students to consistently hear numbers read as decimals, for example 1.7 as one and 7 tenths so that they can connect decimal notation to visual representations and fraction notation. Later, in the lesson synthesis, the connections between the decimal notation and numbers in base-ten will begin to be made explicit.
Students may begin to notice that there are different ways to write decimals that represent the same fraction. It is not essential to discuss this in depth, as students will look at equivalent decimals more closely in upcoming activities.
Supports accessibility for: Visual-Spatial Processing, Organization, Attention
Required Materials
Materials to Gather
Launch
- Groups of 2
- Give students access to colored pencils.
Activity
- “Work on the first problems independently.”
- 3–4 minutes: independent work time
- Pause for a brief whole-class discussion. Display the diagrams in the first problem.
- “What notation can we write to show each fraction? How do we say the fraction in words?”
- Record students’ responses in both notation and words.
- Display the diagrams of one hundredth and one tenth (in the next problem). Explain that the first fraction, \(\frac{1}{100}\), can also be expressed as 0.01 and is still read “1 hundredth”. This form of writing is called decimal notation.
- “What about \(\frac{9}{100}\)?” (nine hundredths, 0.09) “\(\frac{10}{100}\)?” (ten hundredths, 0.10)
- “We know that \(\frac{10}{100}\) can also be expressed as \(\frac{1}{10}\). How do we say it in words and write it in decimal notation?” (one tenth, 0.1)
- “In the numbers written like 0.1 and 0.01, there are decimal points. The digit to the left of the decimal point is in the ones place. The 0 means that there are no ones.”
- “Now try writing the fractions from the first problem as decimals. Then, complete the rest of the activity.”
- 5–6 minutes: independent or partner work time
- Monitor for the ways students write the fractions in the last problem, which may inform how they write corresponding decimals. For instance, they may write:
- mixed numbers (\(1\frac{20}{100}\))
- sums (\(\frac{100}{100} + \frac{20}{100}\) or \(1 + \frac{20}{100}\))
- fractions with no whole numbers (\(\frac{120}{100}\))
Student Facing
Each large square represents 1.
-
What fraction do the shaded parts of each diagram represent? For the last square, shade in some parts and name the fraction it represents.
a. b. c. d. e. f. -
The shaded part of this diagram represents 0.01 or “1 hundredth.”
The shaded parts of this diagram represent 0.10 or “10 hundredths.”
They also represent 0.1 or “1 tenth.”
Numbers like 0.01, 0.10, and 0.1 are written as decimals.Look at the shaded parts of each diagram in the first problem. Write the numbers they represent as decimals.
-
What fraction and decimal do the shaded parts of each diagram represent?
a. b.
Student Response
For access, consult one of our IM Certified Partners.
Advancing Student Thinking
Activity Synthesis
- Invite students to share the decimals for the diagrams in the first problem. Record their responses for all to see.
- “How are the diagrams in the last problem different from those in the first problem?” (They represent numbers greater than 1.)
- “How did you figure out how to write each fraction as a decimal?”
- If not mentioned in students’ responses, point out that we can think of \(1\frac{20}{100}\) as \(1 + \frac{20}{100}\). The 1 whole goes in the ones place, to the left of the decimal point, and the 20 hundredths goes on the right of the decimal point.
- “The decimal 1.20 can be read ‘one and 20 hundredths’. The decimal 1.33 can be read ‘one and 33 hundredths’.”
Activity 2: Ways to Express a Number (15 minutes)
Narrative
In this activity, students practice representing and writing decimals given another representation (fraction notation or a diagram). The idea that two decimals can be equivalent, just like two fractions can be equivalent, is made explicit here. When students make connections between quantities in word form, decimal form, and fraction form, they reason abstractly and quantitatively (MP2).
Advances: Conversing, Reading
Required Materials
Materials to Gather
Launch
- Groups of 2
- Give students access to colored pencils.
- “Let’s practice representing amounts using diagrams, fractions, and decimals.”
Activity
- “Take a few quiet minutes to work on the activity. Then, share your responses with your partner.”
- 7–8 minutes: independent work time
- 3–4 minutes: partner discussion
- Monitor for students who use the idea of equivalent fractions to explain why 0.6 and 0.60 refer to the same amount.
Student Facing
Each large square represents 1.
-
Write a fraction and a decimal that represent the shaded parts of each diagram. Then, write each amount in words.
a. b. c. -
Shade each diagram to represent each given fraction or decimal.
a. Fraction: ________
Decimal: 0.78
b. Fraction: \(\frac{8}{10}\)
Decimal: ________
c. Fraction: \(\frac{55}{100}\)
Decimal: ________
d. Fraction: \(\frac{107}{100}\)
Decimal: ________
e. Fraction: ________
Decimal: 1.6
-
Han and Elena disagree about what number the shaded portion represents.
Han says that it represents 0.60 and Elena says it represents 0.6.
Explain why both Han and Elena are correct.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
- Ask students to use words and decimal notation to express each amount in the first problem.
- Clarify that 0.02 can be named “two hundredths” and 0.22 can be named “twenty-two hundredths” and so on.
- Select students to share their representations for \(\frac{107}{100}\) and 1.6 and how they reasoned about them.
- Display 1.07 and 1.6. “How would you say these decimals in words?” (One and seven hundredths or one point zero seven for 1.07, and one and sixth tenths or one point six for 1.6.)
Lesson Synthesis
Lesson Synthesis
“Today we learned that a fraction can be written as a decimal, regardless of whether it is less or greater than 1.”
Display the number 0.78. Ask students to identify what each digit represents. Annotate the numbers as shown. (Note that students are not expected to do this independently at this time.)
“Why might it make sense to name this decimal seventy-eight hundredths?” (Seven tenths and 8 hundredths is equivalent to 78 hundredths.)
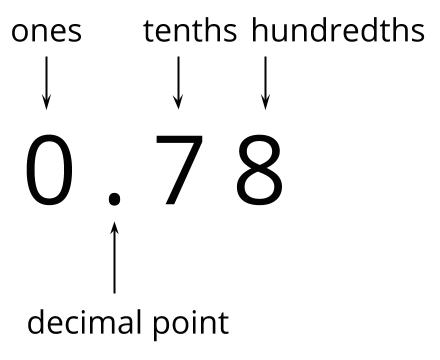
Display the numbers 0.6 and 0.60.
“How do we say these numbers in words?” (Six tenths for 0.6, and sixty hundredths for 0.60)
“In both numbers, what does the 0 to the left of the decimal point represent?” (Zero ones)
“In 0.6, what does the 6 represent?” (Six tenths)
“In 0.60, what does the 60 represent?” (Sixty hundredths)
“Why can we use the same diagram to represent 0.6 and 0.60?” (They represent the same amount. Six tenths is equivalent to sixty hundredths, so 0.6 and 0.60 are equivalent.)
Reiterate that the decimal point separates the whole number and the fractional amount.
Cool-down: What Does It Represent? (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.


















