Lesson 4
Build Fractions from Unit Fractions
Warm-up: Number Talk: 3 and Another Factor (10 minutes)
Narrative
This Number Talk encourages students to look for structure in multiplication expressions and rely on properties of operations to mentally solve problems. Reasoning about products of whole numbers helps to develop students' fluency with multiplication within 100.
Launch
- Display one expression.
- “Give me a signal when you have an answer and can explain how you got it.”
- 1 minute: quiet think time
Activity
- Record answers and strategy.
- Keep expressions and work displayed.
- Repeat with each expression.
Student Facing
Find the value of each expression mentally.
- \(3 \times 3\)
- \(7 \times 3\)
- \(10 \times 3\)
- \(3 \times 17\)
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
- “How did the earlier expressions help you find the value of the last expression?”
- Consider asking:
- “Did anyone have the same strategy but would explain it differently?”
- “Did anyone approach the problem in a different way?”
Activity 1: Introduce Secret Fractions (20 minutes)
Narrative
The purpose of this activity is for students to learn the Secret Fractions center and build non-unit fractions from unit fractions. Students use unit fractions to build “secret fractions,” which are non-unit fractions. For example, to complete a secret fraction card with \(\frac{3}{4}\), students need three cards with \(\frac{1}{4}\). After completing each secret fraction, they reveal the fraction they’ve made and shade the gameboard to represent it. The synthesis highlights strategies students used to build their non-unit fractions.
Here are the images of the cards for reference and planning:
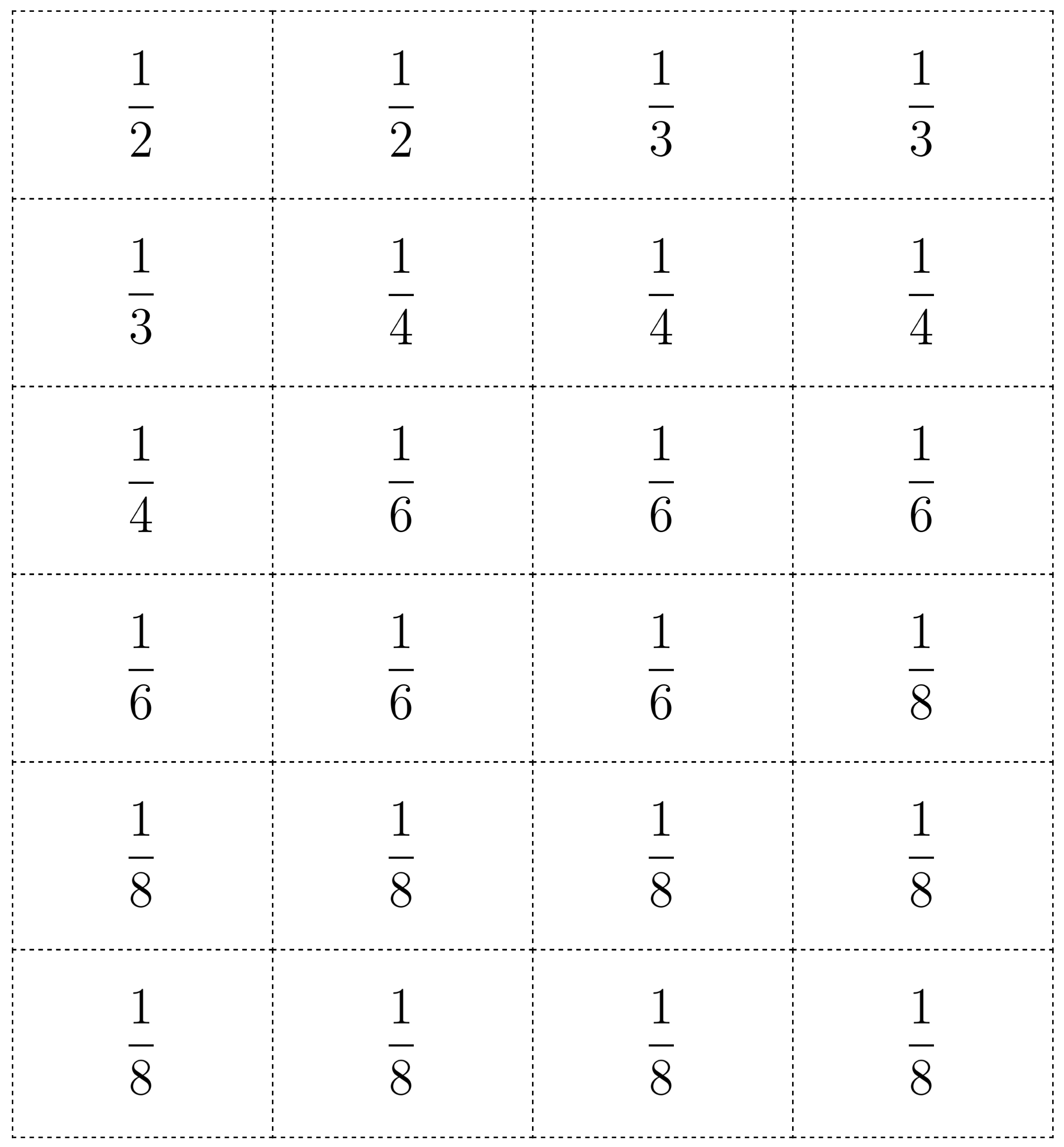
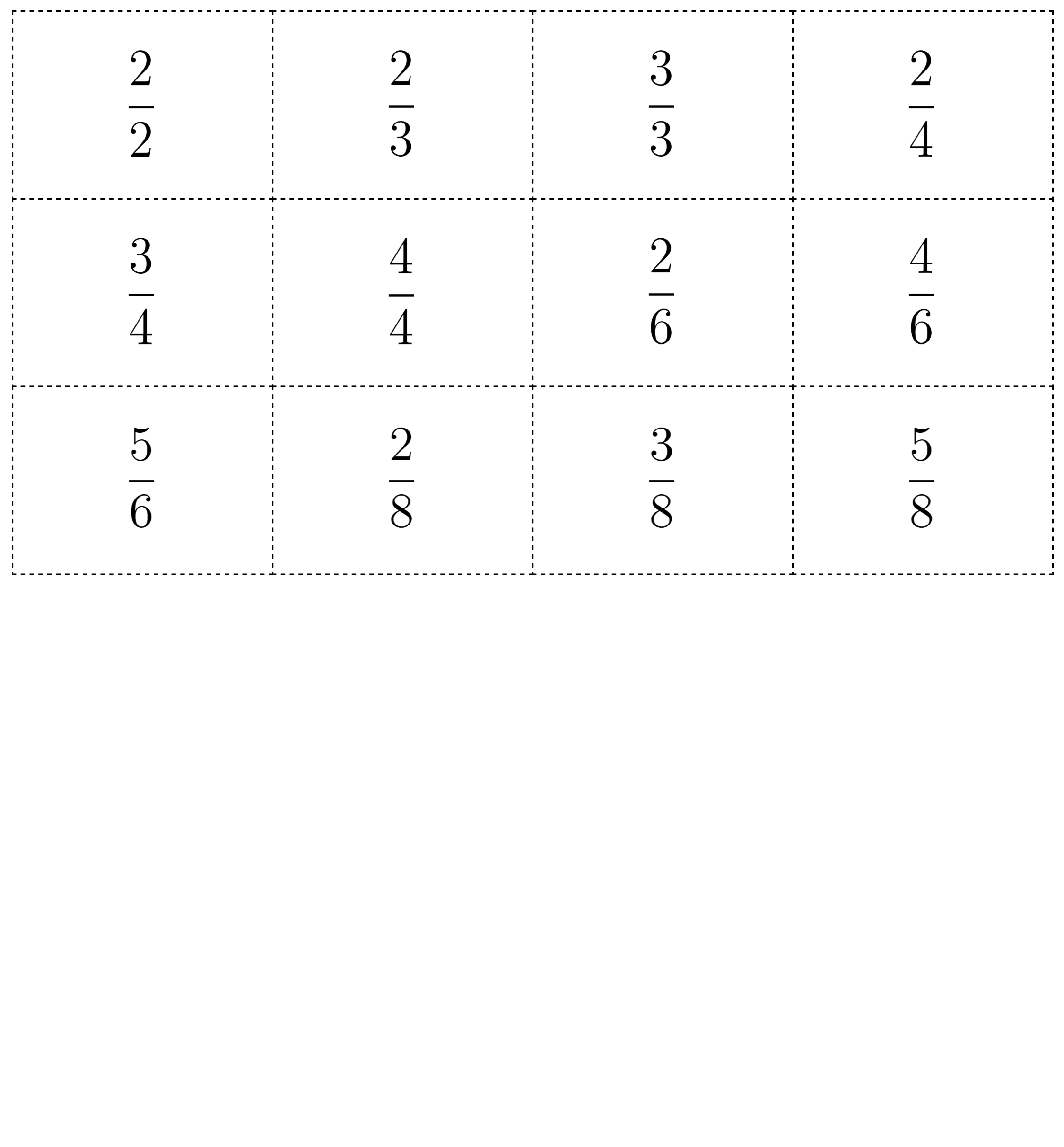
Supports accessibility for: Social-Emotional Functioning
Required Materials
Materials to Gather
Materials to Copy
- Secret Fractions Stage 1 Gameboard
- Secret Fractions Stage 1 Cards
Required Preparation
- Create a set of cards from the blackline master for each group of 2.
- Print extra gameboards for the launch and groups that have time for an extra game.
- Students might want a folder or divider so their partner doesn’t see their cards.
Launch
- Groups of 2
- Give each group a set of cards and a gameboard.
- “We’re going to play a game called Secret Fractions. Let’s read through the directions and play 1 round together.”
- Read through the directions with the class and play a round against the class, displaying the fractions from the cards and thinking through decisions aloud.
- Show students how to place an object, such as a folder, between them to obstruct the view of the other player.
- Give each group that wants a divider a folder or other divider.
Activity
- “Now, play Secret Fractions with your partner.”
- 10–15 minutes: partner work time
- Monitor for students who:
- trade their secret fractions for new ones because most of their unit fractions have a different denominator
- keep track of the unit fractions they have as they try to make their non-unit fractions
Student Facing
The goal of the game is to be the first to build 2 secret fractions with unit fractions.
- Make two stacks: one for secret fractions and one for unit fractions. Place all cards face down.
- Each player draws 2 secret fraction cards. These are the fractions you are trying to make with your unit fractions.
-
On your turn, you can make one of these moves:
- Pick up 1 unit fraction card.
- Trade both of your secret fractions for 2 new secret fractions from the stack.
- When you have enough unit fractions to make one of your secret fractions, shade your gameboard to represent your secret fraction. Then, pick a new secret fraction.
- The first player to make 2 secret fractions wins.

Activity Synthesis
- “What strategies did you find helpful for building your secret fractions?” (When \(\frac{5}{8}\) was my secret fraction, I was keeping track of how many \(\frac{1}{8}\) cards I had to make \(\frac{5}{8}\). When I had \(\frac{3}{4}\) as a secret fraction, I knew I needed \(\frac{1}{4}\) cards, but I had a bunch of \(\frac{1}{6}\) cards, so I traded for different secret fractions.)
Activity 2: Represent Fraction Situations (15 minutes)
Narrative
The purpose of this activity is for students to use diagrams to represent situations that involve non-unit fractions. The synthesis focuses on how students partition and shade the diagrams and how the end of the shaded portion could represent the location of an object. When students interpret the different situations in terms of the diagrams they reason abstractly and quantitatively (MP2).
Advances: Speaking, Representing
Required Materials
Materials to Gather
Launch
- Groups of 2
- “What are some games that you like to play with friends?”
- Share responses.
- “Pilolo is a game played in Ghana. One player hides sticks, rocks, or pennies. The other players have to find one of the objects and be the first to reach the finish line to get a point. Look at the picture of some children playing Pilolo and think about some strategies you might use if you played this game.” (I would try to hide the objects in a good hiding spot. I would run fast to be the first one to the finish line.)
- 30 seconds: quiet think time
- Share responses.
- “We’re going to represent some situations about students playing Pilolo.”
Activity
- “In the activity, each strip represents the length of a street where Pilolo is played.”
- “Work independently to represent each situation on a diagram.”
- 3–5 minutes: independent work time
- “With a partner, choose one of the situations and make a poster to show how you represented the situation with a fraction strip. You may want to include details such as notes, drawings, labels, and so on, to help others understand your thinking.”
- Give students materials for creating a visual display.
- 5–7 minutes: partner work time
Student Facing
Here are four situations about playing Pilolo and four diagrams. Each diagram represents the length of a street where the game is played.
Represent each situation on a diagram. Be prepared to explain your reasoning.
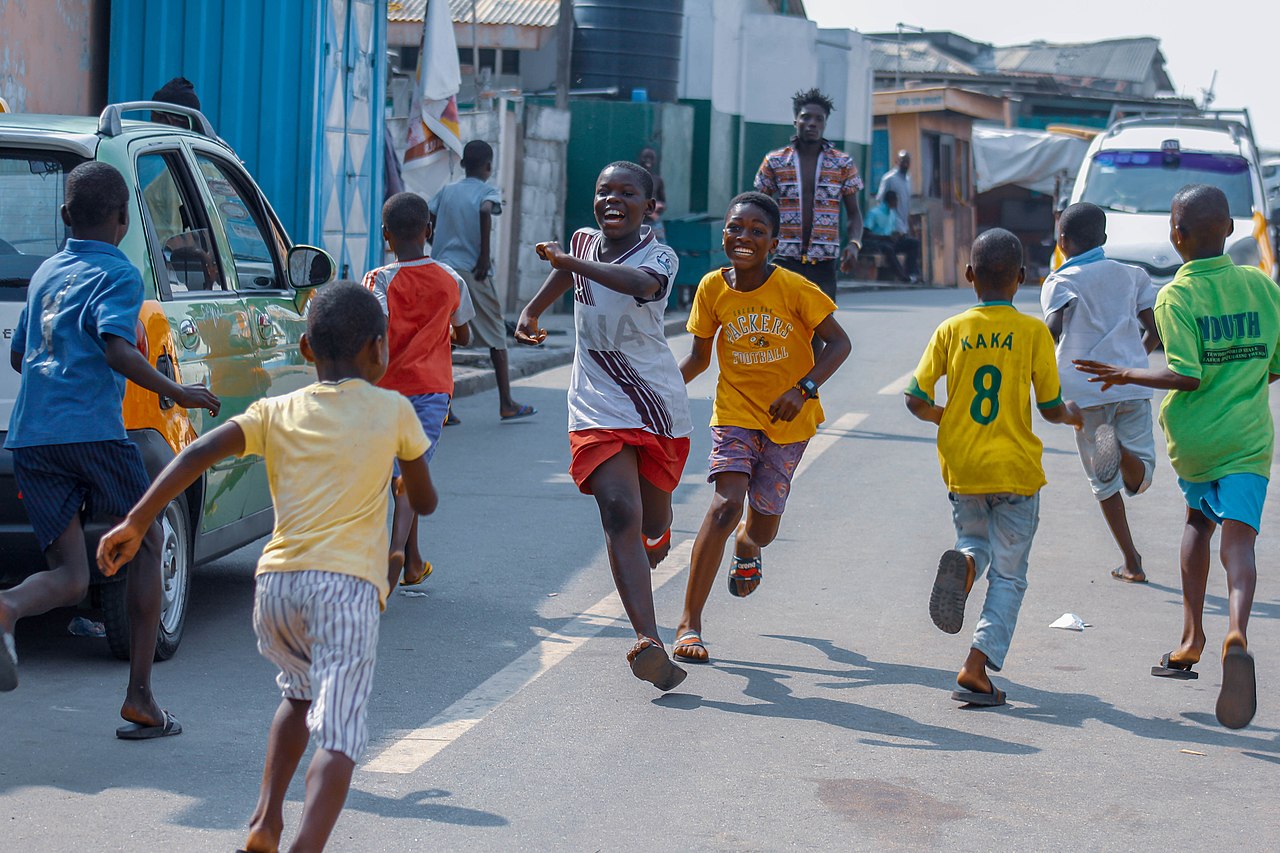
-
A student walks \(\frac{4}{8}\) the length of the street and hides a rock.
-
A student walks \(\frac{2}{3}\) the length of the street and hides a penny.
-
A student walks \(\frac{3}{4}\) the length of the street and hides a stick.
-
A student walks \(\frac{5}{6}\) the length of the street and hides a penny.
- This diagram represents the location of a hidden stick.
Student Response
For access, consult one of our IM Certified Partners.
Advancing Student Thinking
- “How did you partition the strip into sixths? Eighths?”
- “How could you use thirds to partition into sixths? Use fourths to partition into eighths?”
Activity Synthesis
- Display posters around the room.
- “As you look at each poster, discuss how each situation was shown on the diagram.” (The diagram was partitioned into 6 equal parts. 5 of the equal parts were shaded.)
- 2–3 minutes: partner discussion
- Share responses.
- “What part of each diagram would represent where the object was hidden?” (The end of the shaded part.)
Lesson Synthesis
Lesson Synthesis
Display some completed gameboards from the first activity and one of the diagrams that represents a situation from the second activity.
“How was making the fractions in the game like representing the situations? How was it different?” (The parts had to be equal-sized for both activities. We had to count the parts in both activities. The fractions were made from unit fractions. In the first activity, we had the pieces to build the fraction, but in the second activity, we had to partition and shade in the parts to make the fraction.)
“In both activities we were able to see how unit fractions are used to make other fractions.”
Cool-down: Represent a Fraction (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Section Summary
Student Facing
In this section, we learned how to partition shapes into halves, thirds, fourths, sixths, and eighths, and how to describe each of those parts in words and using a number.





The numbers we use to describe these equal-sized parts are fractions.
A fraction like \(\frac{1}{4}\) is read “one-fourth” because it represents one of the 4 equal parts in a whole.

A fraction like \(\frac{3}{4}\) is read “three-fourths” because it represents 3 parts that are each one-fourth or \(\frac{1}{4}\) in size.

Fractions that refer to only one of the equal parts in a whole— like \(\frac{1}{2}\), \(\frac{1}{3}\), \(\frac{1}{8}\)—are called unit fractions.
We learned that the bottom part of the fraction tells us how many equal parts we partitioned the whole into. The top part of the fraction tells us how many of the equal parts are being described.

