Lesson 3
Non-unit Fractions
Warm-up: Notice and Wonder: More than One Part (10 minutes)
Narrative
The purpose of this warm-up is to elicit the idea that we can think about multiple equal parts in a diagram and use fractions to refer to them, which will be useful when students identify fractions in diagrams and shade diagrams to show a specific fraction in a later activity. While students may notice and wonder many things about these images, the fact that more than one of the equal parts of the square is shaded, there is a fraction underneath the third diagram, and how the shaded parts could be described are the important discussion points.
When students articulate what they notice and wonder, they have an opportunity to attend to precision in the language they use to describe what they see (MP6). They might first propose less formal or imprecise language, and then restate their observation with more precise language in order to communicate more clearly.
Launch
- Groups of 2
- Display the image.
- “What do you notice? What do you wonder?”
- 1 minute: quiet think time
Activity
- “Discuss your thinking with your partner.”
- 1 minute: partner discussion
- Share and record responses.
Student Facing
What do you notice? What do you wonder?

Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
- “What do you think the 3 and the 4 stand for in the number below the third square?” (The 4 stands for the 4 equal parts in the square. The 3 stands for the number of parts that are shaded.)
- “Sometimes we may want to talk about more than one part and we can describe those parts with a number.”
- “What do we call the parts in each square?” (Fourths)
- “How many fourths are shaded in the first square?” (1)
- “How many fourths are shaded in the second square? Third square?” (2 and 3)
- “How many fourths are shaded in the last image?” (4)
- “We can refer to the shaded parts in each image by describing the number of fourths: one fourth, two fourths, three fourths, and four fourths.”
- “We’ll look at how to write these amounts in the next activity.”
Activity 1: Write and Read Fractions (15 minutes)
Narrative
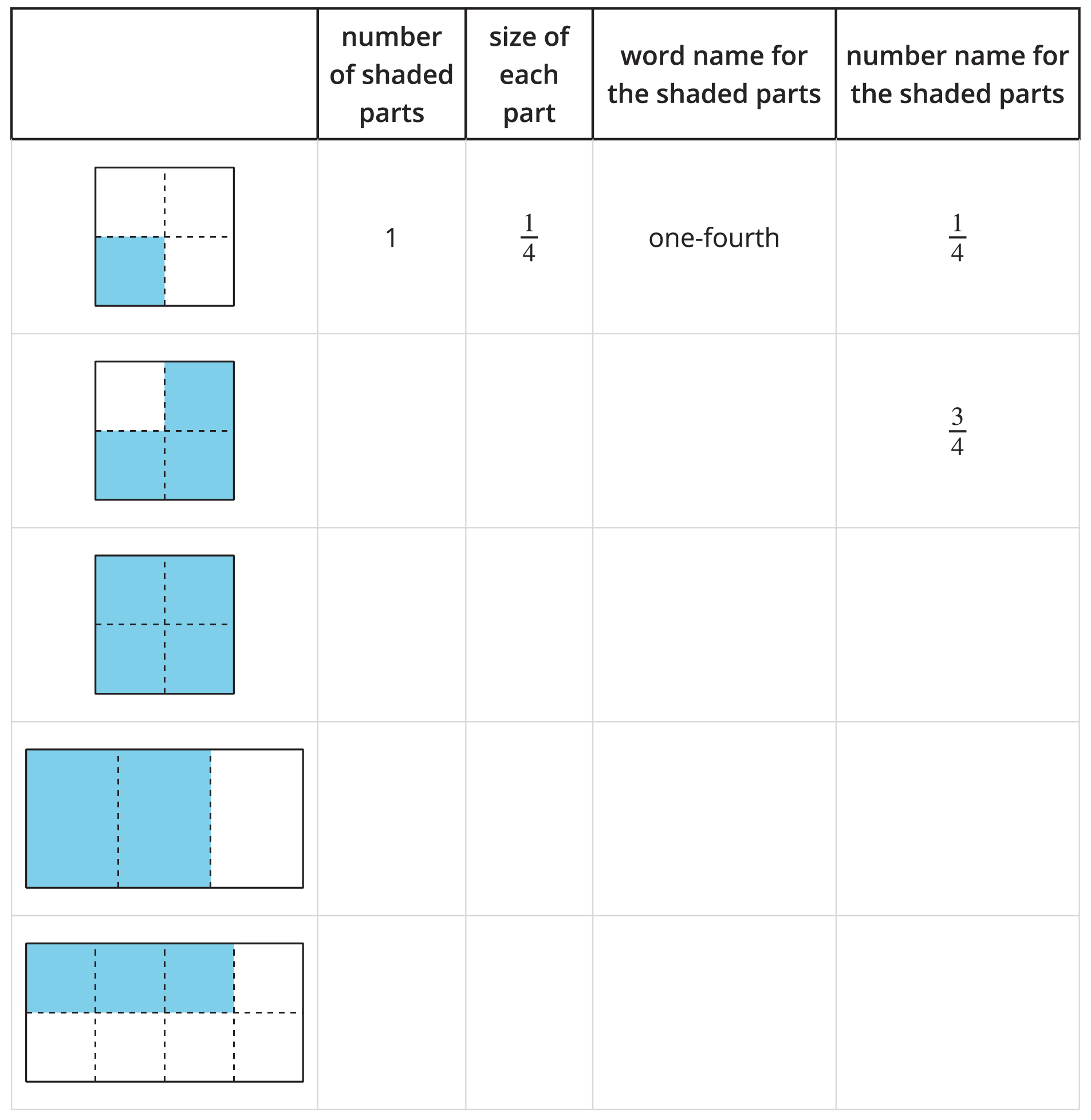
The purpose of this activity is for students to make sense of non-unit fractions and the notation used to describe them. They learn that the denominator tells the number of equal parts the whole was partitioned into and the numerator tells the number of parts that are being described. Students write non-unit fractions that represent the shaded portions of area diagrams.
If needed, especially with the fractions greater than one, clarify that each rectangle represents one whole. The activity concludes with students practicing how to read non-unit fractions. The terms “numerator” and “denominator” will be introduced in a later lesson.
When students notice that the bottom part of the fraction stays the same and the top part of the fraction changes, representing the number of equal parts that are shaded, they look for and make use of structure (MP7).
Launch
- Groups of 2
- Display the table.
- “Let's look at the first table.”
- “The first three images are the squares we saw earlier. Let's name them again.” (One-fourth, three-fourths, four-fourths)
- “Let’s complete the second row of the table together. This is the square we just worked with in the warm-up and the number that represents the total amount shaded is already in the table. How many of the parts are shaded?” (Three)
- “What is the size of each part?” (\(\frac{1}{4}\))
- “Write ‘three-fourths’ to record how we read this fraction.”
Activity
- “Work with your partner to complete the table.”
- 5–7 minutes: partner work time
Student Facing
Each shape in each row of the table represents 1. Use the shaded parts to complete the missing information in the table. Be prepared to explain your reasoning.

Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
- Display the completed table.
- “Now that the table is complete, what do you notice? What do you wonder?” (The size of each part always has a 1 in the top part of the fraction. The bottom part of the fraction is the same for each part and the total amount shaded. The top part of the fraction is how many parts are shaded.)
- “Let’s think about how we should describe or name the shaded parts in each image.”
- 30 seconds: quiet think time
- Invite students to name the shaded parts in each image.
- As students name the shaded part in each image, have them share how they recorded the name using fraction notation.
Activity 2: Fraction Match (20 minutes)
Narrative
The purpose of this activity is for students to match fractions to shaded diagrams. Reiterate that each rectangle represents one whole. After one round of matching, students pause to create 4 new pairs of cards to add to their set. Give students the Fraction Match Part 2 cards when they create their own pairs of cards.
Students observe and use structure as they identify that the top number in the fraction represents the number of shaded pieces while the bottom number represents the number of those pieces in one whole rectangle (MP7).
Advances: Speaking, Representing
Supports accessibility for: Memory, Social-Emotional Functioning
Required Materials
Materials to Copy
- Fraction Match Part 1
- Fraction Match Part 2
Required Preparation
- Create a set of cards from the Fraction Match Part 1 blackline master for each group of 2.
- Create a set of 8 cards from the Fraction Match Part 2 blackline master for each group of 2.
Launch
- Groups of 2
- “We’re going to play a game in which you match fractions and diagrams. Read the directions to the game with your partner and discuss any questions you have about the game.”
- Answer any questions about the game.
- Give each group one set of cards created from Fraction Match Part 1.
Activity
- “Play one round of Fraction Match with your partner.”
- 5–7 minutes: partner work time
- Give each group one set of Fraction Match Part 2.
- “Before you play another round, work with your partner to create 4 new pairs of cards to add to the set. Partition and shade a diagram to match each fraction.”
- 3–5 minutes: partner work time
- “Now, play another round of fraction match with your partner using all the cards.”
- 5–7 minutes: partner work time
- Monitor for students who notice that \(\frac{3}{3}\) means the whole rectangle is shaded.
Student Facing
Your teacher will give you a set of cards for playing Fraction Match. Two cards are a match if one is a diagram and the other a number, but they have the same value.
-
To play Fraction Match:
- Arrange the cards face down in an array.
- Take turns choosing 2 cards. If the cards match, keep them and go again. If not, return them to where they were, face down. You can’t keep more than 2 matches on each turn.
- After all the matches have been found, the player with the most cards wins.
- Use the cards your teacher gives you to create 4 new pairs of cards to add to the set.
- Play another round of Fraction Match using all the cards.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
- Ask 1–2 groups to display a rectangle they partitioned and shaded to match one of the fractions.
- For each rectangle students share, discuss the fraction that it represents.
- Display a diagram of \(\frac{3}{3}\) with all the parts shaded.
- “_____ noticed that to show \(\frac{3}{3}\), we have to shade the whole rectangle. Look back over both activities for other fractions that are shown by shading the whole rectangle.” (\(\frac{2}{2}\), \(\frac{4}{4}\), and \(\frac{6}{6}\))
- Consider asking: “How many _____s would it take to make a whole? How do you know?”
- “These fractions are equivalent to 1 because they represent all the parts of the whole. We’ll work with other fractions like this as we learn about fractions.”
Lesson Synthesis
Lesson Synthesis
Display: \(\frac{1}{8}\) and \(\frac{5}{8}\)
“Today we learned how to build more fractions, like \(\frac{5}{8}\), from fractions we already knew, like \(\frac{1}{8}\). We call fractions, like \(\frac{1}{8}\), that describe one equal-sized part, unit fractions. How did you see unit fractions helping us build new fractions today?” (Every fraction we worked with today was made up of unit fractions. If we shade more than one unit fraction in a rectangle, we get a new fraction that doesn’t have a one on the top of the number.)
Display:
\(\frac{5}{8}\)

“Look at the fraction \(\frac{5}{8}\). What does each part of the number tell us?” (The 8 tells us how many parts the rectangle is being split into and what size they are. There are 8 one-eighth parts. The 5 tells us how many of the parts are shaded. Five of the one-eighth parts will be shaded.)
Display:
\(\frac{7}{6}\)

“Look at the fraction \(\frac{7}{6}\). What does each part of the number tell us?” (The 6 tells us how many parts each rectangle is being split into and what size they are. There are 6 one-sixth parts in each rectangle. The 7 tells us how many of the parts are shaded. Seven of the one-sixth parts will be shaded.)
Cool-down: Shaded Fraction (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.