Lesson 13
Whole Numbers and Fractions
Warm-up: Notice and Wonder: Four Number Lines (10 minutes)
Narrative
This warm-up elicits observations about the different ways whole numbers can be expressed as fractions. Students have previously seen number lines where 1, 2, and 3 were labeled with fractions in halves, thirds, fourths, sixths, and eighths. They understand that a denominator of 2 corresponds to 2 equal parts in the length representing 1 whole. The number line marked with \(\frac{1}{1}\), \(\frac{2}{1}\), and \(\frac{3}{1}\) is shown together with those marked with halves, thirds, and fourths to highlight that a denominator of 1 means each whole has 1 part.
In the synthesis, students learn that fractions with 1 as a denominator can be used to represent whole numbers (\(\frac{2}{1} = 2\)).
Launch
- Groups of 2
- Display the image.
- “What do you notice? What do you wonder?”
- 1 minute: quiet think time
Activity
- “Discuss your thinking with your partner.”
- 1 minute: partner discussion
- Share and record responses.
Student Facing
What do you notice? What do you wonder?

Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
- “What could it mean to have a denominator of 1?” (The whole hasn’t been partitioned. The whole has been partitioned into 1 part.)
- Have students label the locations of \(\frac{1}{1}\), \(\frac{2}{1}\), and \(\frac{3}{1}\) on the first number line with 1, 2, and 3.

- “The length from 0 to 1 hasn’t been partitioned, so each part has a length of 1. This is what a denominator of 1 means. If we have 1 part of 1, the numerator is 1. If we have 2 parts of 1, the numerator is 2, and so on.”
- “What other fractions on these number lines might be equivalent to 1?” (\(\frac{2}{2}\), \(\frac{3}{3}\), \(\frac{4}{4}\))
Activity 1: Hidden Whole Numbers (20 minutes)
Narrative
In an earlier lesson, students saw that whole numbers could be written as fractions. The purpose of this activity is for students to recognize fractions that are equivalent to whole numbers, using patterns in number lines to support their reasoning. To identify fractions that are equivalent to whole numbers on number lines, students may:
- Use what they know about 2 halves, 3 thirds, and 4 fourths to identify 1, and then circle fractions at the same intervals down each number line.
- Use what they know about 2 halves, 4 halves, and 6 halves to identify 1, 2, and 3 on the first number line, and then circle fractions in the same locations on other number lines.
- Use the relationship between parts and wholes (for instance, 3 thirds make 1, 6 thirds make 2, and 9 thirds make 3).
Students then record equations that show fractions that are equivalent to whole numbers. Finally, given a list of fractions, students determine which ones are equivalent to whole numbers.
When students use patterns to identify fractions that are equivalent to whole numbers, they look for and express regularity in repeated reasoning (MP8).
Supports accessibility for: Organization, Attention, Social-emotional skills
Launch
- Groups of 2
- “Work with your partner to circle all the fractions that are equivalent to whole numbers. Be sure to explain your reasoning.”
- 2–3 minutes: partner work time
- “Look at the fractions you circled. How did you know which ones to circle?”
- 1–2 minutes: partner discussion
- Share responses.
Activity
- “We can use equations like \(\frac{4}{2}=2\) to show that \(\frac{4}{2}\) and 2 are at the same location on the number line, so they are equivalent.”
- “Work independently to complete the second and third problem.”
- 5–7 minutes: independent work time
- “Share your solutions to the second and third problems with your partner. Be sure to share your reasoning.”
- 2–3 minutes: partner discussion
Student Facing
-
On each number line, circle the fractions that are equivalent to whole numbers. Explain how you know.
-
We can write \(\frac{4}{2}=2\) to show that \(\frac{4}{2}\) and 2 are at the same location on the number line, so they are equivalent.
Write 5 other equations that show fractions that are equivalent to whole numbers. Use the number lines if they are helpful.
-
Decide if each fraction is equivalent to a whole number. Use number lines if they are helpful.
- \(\frac{11}{2}\)
- \(\frac{5}{1}\)
- \(\frac{12}{6}\)
- \(\frac{10}{3}\)
- \(\frac{12}{8}\)
- \(\frac{16}{4}\)
Student Response
For access, consult one of our IM Certified Partners.
Advancing Student Thinking
- “Tell me about the fractions on the number line.”
- “How could you use the partitions in 1 whole to find the fractions at 2? At 3?”
Activity Synthesis
- Invite students to share their responses and reasoning for the last set of problems.
- As students share, record fractions that are equivalent to whole numbers as equations and highlight that equations can be written starting with the whole number or fraction (for example, \(\frac{12}{6}=2\) or \(2=\frac{12}{6}\)).
- “How did you know if each fraction was equivalent to a whole number?”
- “What patterns do you see that could be helpful for finding more fractions that are whole numbers?”
- Highlight strategies that are based on understanding of the number of equal parts that are in 1 whole and on observed patterns. (For instance, the thirds that are equivalent to whole numbers have a numerator that is a number we get when counting by 3.)
Activity 2: Write Them as Fractions (15 minutes)
Narrative
The purpose of this activity is for students to write whole numbers as fractions. Students may reason in any way that makes sense to them, including using patterns they noticed previously. When students observe patterns as they write whole numbers as fractions, they look for and make use of structure (MP7).
This activity uses a “carousel” structure in which students complete a rotation of tasks. Consider demonstrating the steps before students begin.
Advances: Speaking, Representing
Launch
- Groups of 3
- “Take a moment to look at the table and the numbers in the table. How do you think the table works?”
- 1 minute: quiet think time
- Share responses.
- “In your group, take turns explaining why \(\frac{4}{1}\) is equivalent to 4, \(\frac{30}{6}\) is equivalent to 5, and \(\frac{48}{8}\) is equivalent to 6.”
- 2 minutes: group discussion
Activity
- “Work with your group to complete the table. Start by writing two fractions that are equivalent to each whole number: 4, 5, and 6.”
- 2 minutes: independent work time
- “Pass your paper to your right. On the paper your receive, write one new fraction that is equivalent to a whole number of your choice.”
- “Keep passing and writing one additional fraction for a whole number until the table is complete.”
- Encourage students to ask clarifying questions before they begin.
- 7–8 minutes: group work time
- “Be prepared to explain how you know what fractions to write for each whole number.”
- Monitor for students who:
- use a number line (either draw a new one or extending those from an earlier activity)
- extend a pattern they noticed in fractions that are equivalent to whole numbers
- use multiplication facts
Student Facing
Work with your group to complete the table. In each column, write fractions that are equivalent to the whole number in the top row.
- Step 1: Write two fractions that are equivalent to each whole number (six fractions in all). Pass your paper to your right.
- Step 2: When you receive your neighbor’s paper, write a new fraction that is equivalent to a whole number.
- Repeat Step 2 until the table is complete.
| 4 | 5 | 6 |
|---|---|---|
| \(\frac{\large{4}}{\large{1}}\) | ||
| \(\frac{\phantom{\huge000}}{\large{2}}\) | ||
| \(\frac{\phantom{\huge000}}{\large{3}}\) | ||
| \(\frac{\phantom{\huge000}}{\large{4}}\) | ||
| \(\frac{\large{30}}{\large{6}}\) | ||
| \(\frac{\large{48}}{\large{8}}\) |
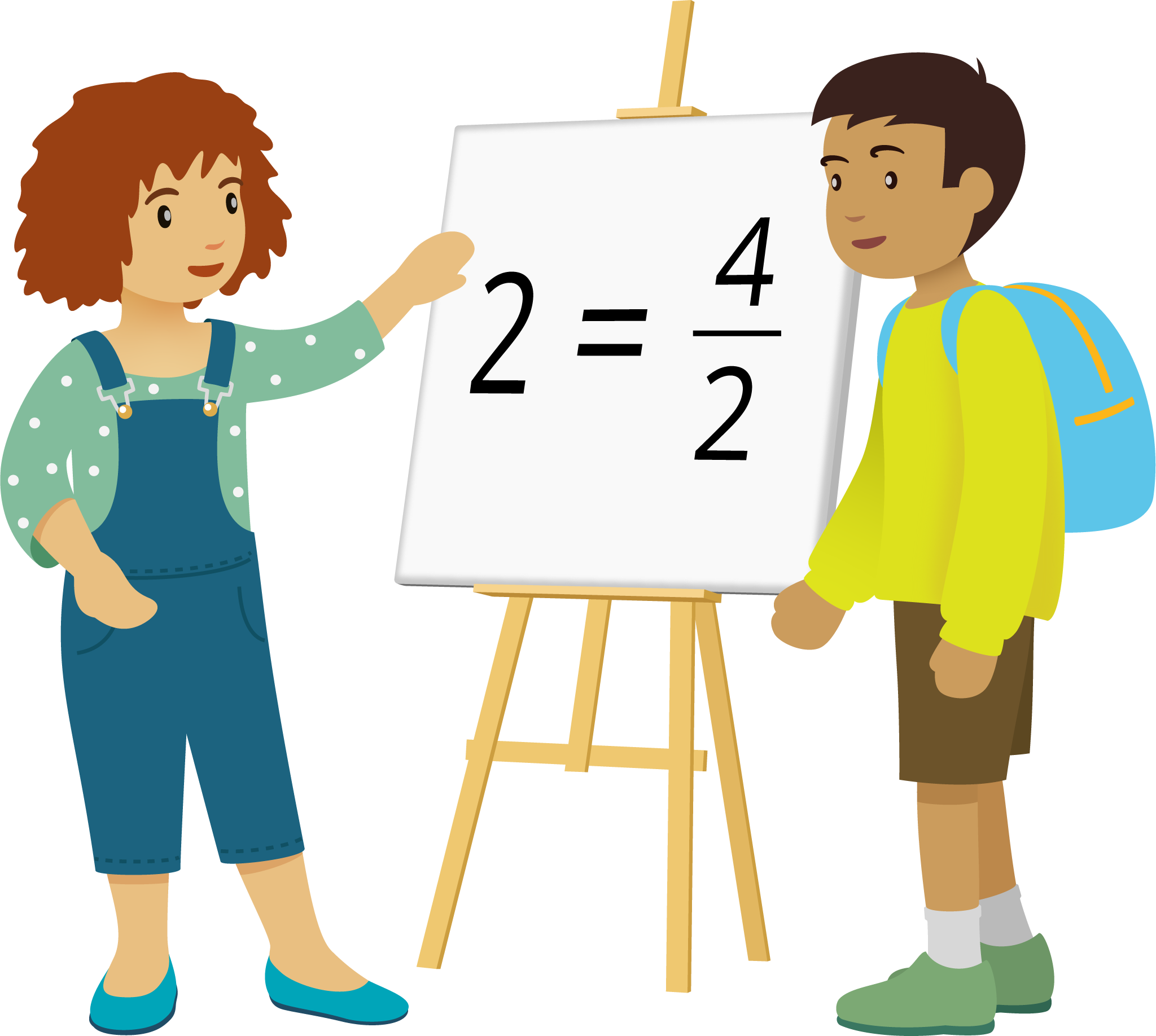
Student Response
For access, consult one of our IM Certified Partners.
Advancing Student Thinking
If students don’t write a whole number as a fraction, consider asking:
- “Tell me about how you would write 1 as a fraction.”
- “How could you use the fraction that's equivalent to 1 to write this number as a fraction?”
Activity Synthesis
- Invite a group of students to display their completed table.
- Select previously identified students to share how they knew what fractions to write for each whole number.
- Invite the class to share other strategies for generating equivalent fractions.
- “What new patterns do you notice in the completed table?” (Sample responses:
- In fractions that are equivalent to 4, you can get the numerator by skip-counting by the denominator 4 times.
- In the row with thirds, the numerator increases by 3. In the row for fourths, it increases by 4.)
Lesson Synthesis
Lesson Synthesis
“Over the last few lessons, we’ve learned about equivalent fractions.”
“What are some important things you’ve learned about fraction equivalence?” (Fractions that are the same size are equivalent. Fractions at the same point on the number line are equivalent. Some fractions are equivalent to whole numbers, but some are not. Whole numbers can be written as fractions.)
Cool-down: Fraction to Whole Number and Whole Number to Fraction (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Section Summary
Student Facing


\(\frac{1}{3} = \frac{2}{6}\)

\(\frac{6}{8} = \frac{3}{4}\)

\(4 = \frac{12}{3}\)



