Lesson 4
Tables, Equations, and Graphs of Functions
4.1: Notice and Wonder: Doubling Back (5 minutes)
Warm-up
The purpose of this warm-up is to familiarize students with one of the central graphical representations they will be working with in the lesson. As students notice and wonder, they have the opportunity to reason abstractly and quantitatively if they consider the situation the graph represents (MP2).
Launch
Tell students they will look at a graph, and their job is to think of at least one thing they notice and at least one thing they wonder about the picture. Display the graph for all to see and give 1 minute of quiet think time. Ask students to give a signal when they have noticed or wondered about something.
Student Facing
What do you notice? What do you wonder?
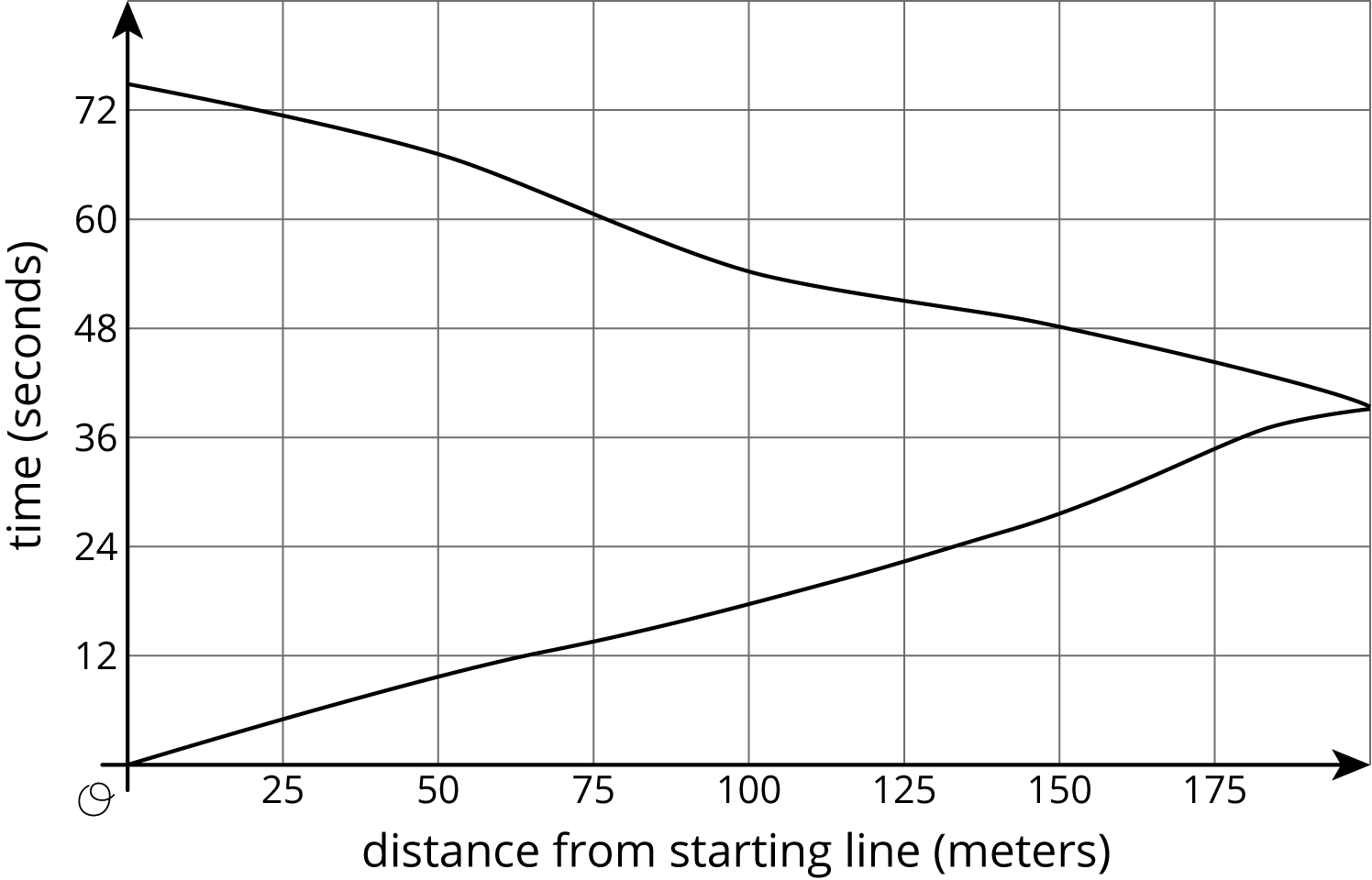
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Ask students to share things they noticed and wondered about the graph. Record and display these ideas for all to see. For each of the things students notice and wonder, ask them to reference the graph in their explanation. If no one notices that at every distance from the starting line, there are two associated times (except at 200 meters), bring that to their attention.
If there is time, ask students to make some estimations or guesses for the wonders that refer to the information in the graph. For example, if someone wonders what the title of the graph may be, ask them to create a title that would make sense for this context.
4.2: Equations and Graphs of Functions (15 minutes)
Activity
The purpose of this activity is for students to connect different function representations and learn the conventions used to label a graph of a function. Students first match function contexts and equations to graphs. They next label the axes and calculate input-output pairs for each function. The focus of the discussion should be on what quantities students used to label the axes and recognizing the placement of the independent or dependent variables on the axes.
Monitor for students who recognize that there is one graph that is not linear and match that graph with the equation that is not linear.
Launch
Arrange students in groups of 2. Display the graph for all to see. Ask students to consider what the graph might represent.
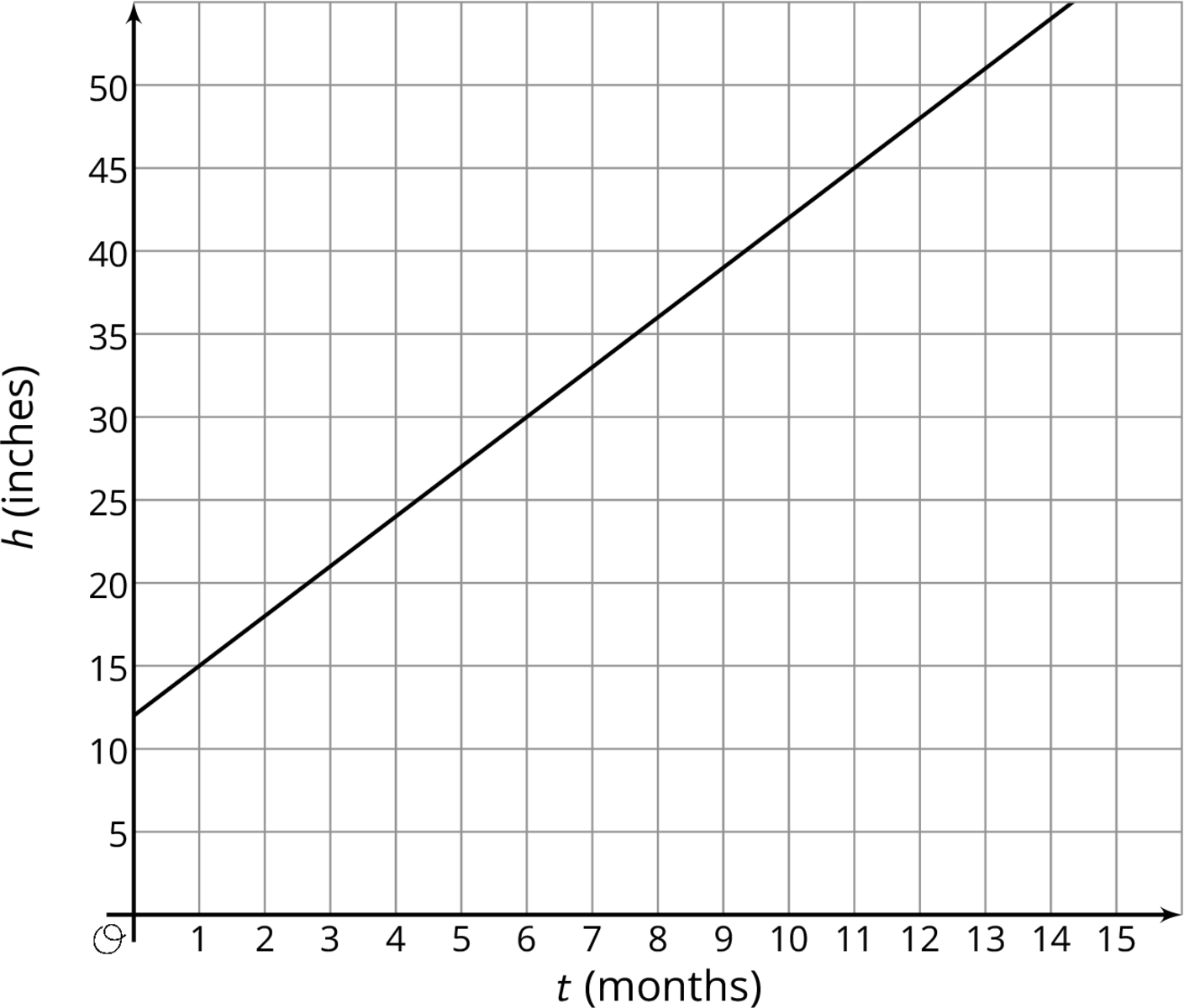
After brief quiet think time, select 1–2 students to share their ideas. (For example, something starts at 12 inches and grows 15 inches for every 5 months that pass.)
Remind students that axes labels help us determine what quantities are represented and should always be included. Let them know that in this activity the graphs of three functions have been started, but the labels are missing and part of their work is to figure out what those labels are meant to be.
Give students 3–5 minutes of quiet work time and then time to share responses with their partner. Encourage students to compare their explanations for the last three problems and resolve any differences. Follow with a whole-class discussion.
Supports accessibility for: Visual-spatial processing
Design Principle(s): Optimize output (for explanation)
Student Facing
The graphs of three functions are shown.
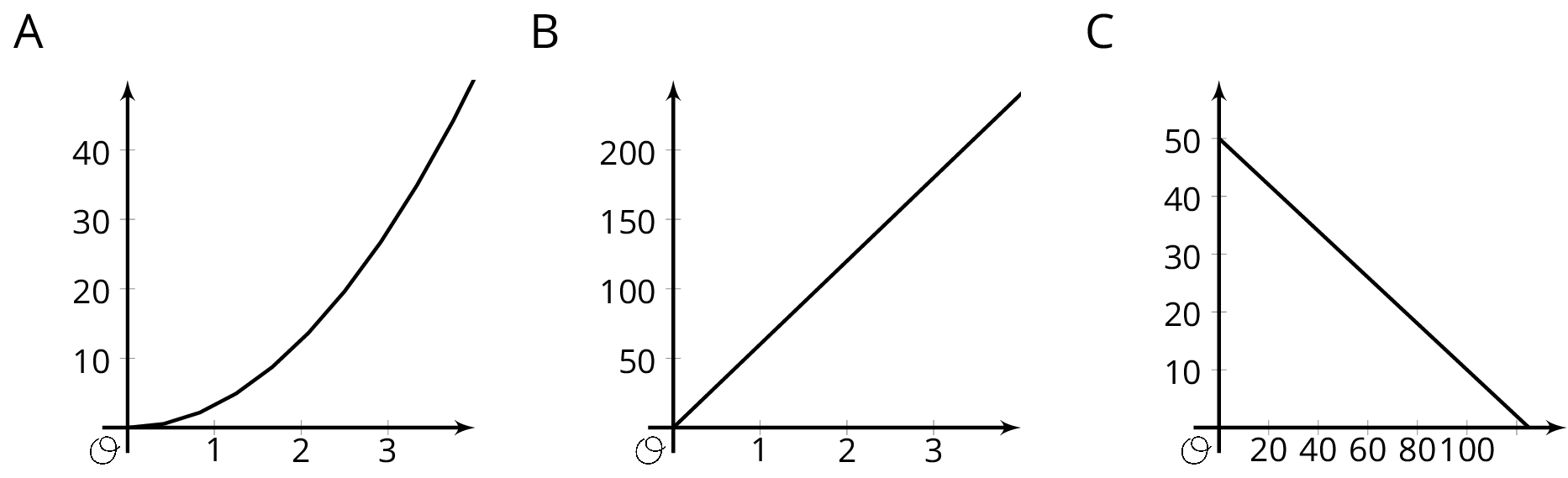
- Match one of these equations to each of the graphs.
- \(d=60t\), where \(d\) is the distance in miles that you would travel in \(t\) hours if you drove at 60 miles per hour.
- \(q = 50-0.4d\), where \(q\) is the number of quarters, and \(d\) is the number of dimes, in a pile of coins worth $12.50.
- \(A = \pi r^2\), where \(A\) is the area in square centimeters of a circle with radius \(r\) centimeters.
- Label each of the axes with the independent and dependent variables and the quantities they represent.
- For each function: What is the output when the input is 1? What does this tell you about the situation? Label the corresponding point on the graph.
- Find two more input-output pairs. What do they tell you about the situation? Label the corresponding points on the graph.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
A function inputs fractions \(\frac{a}{b}\) between 0 and 1 where \(a\) and \(b\) have no common factors, and outputs the fraction \(\frac{1}{b}\). For example, given the input \(\frac34\) the function outputs \(\frac14\), and to the input \(\frac12\) the function outputs \(\frac12\). These two input-output pairs are shown on the graph.
Plot at least 10 more points on the graph of this function. Are most points on the graph above or below a height of \(0.3\)? Of height \(0.01\)?
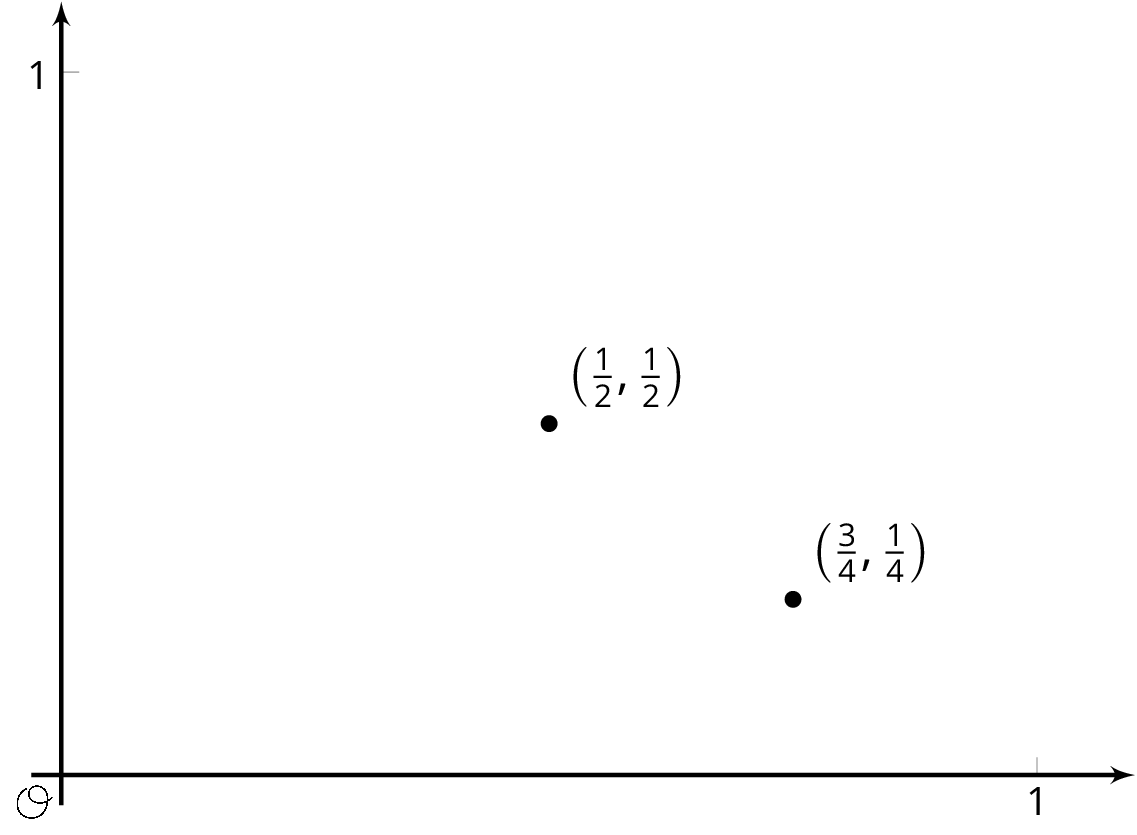
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
The purpose of this discussion is for students to understand the conventions of constructing a graph of a function and where input and outputs are found on a graph. Select students previously identified to share how they figured out \(A=\pi r^2\) matched the non-linear graph.
Ask students:
- “Where are the independent variables labeled on the graphs?” (The horizontal axis)
- “Where are the dependent variables labeled on the graphs?” (The vertical axis)
Tell students that by convention, the independent variable is on the horizontal axis and the dependent variable is on the vertical axis. This means that when we write coordinate pairs, they are in the form of (input, output). For some functions, like the one with quarters and dimes, we can choose which variable is the independent and which is the dependent, which means the graph could be constructed either way based on our decisions.
Conclude the discussion by asking students to share their explanations for the point \((1, 49.6)\) for graph C. (There is no such thing as 0.6 of a quarter.) Remind students that sometimes we have to restrict inputs to only those that make sense. Since it's not possible to have 49.6 quarters, an input of 1 dime does not make sense. Similarly, 2, 3, or 4 dimes result in numbers of quarters that do not make sense. 0 dimes or 5 dimes, however, do produce outputs that make sense. Sometimes it is easier to sketch a graph of the line even when graphing discrete points would be more accurate for the context. Keeping the context of a function in mind is important when making sense of the input-output pairs associated with the function.
4.3: Running around a Track (15 minutes)
Activity
The purpose of this activity is for students to interpret coordinates on graphs of functions and non-functions as well as understand that context does not dictate the independent and dependent variables.
In the first problem time is a function of distance, and the graph and table help determine how long it takes for Kiran to run a specific distance. In the second problem, however, time is not a function of Priya's distance from the starting line. This results in a graph where each input does not give exactly one output.
Launch
Give students 3–5 minutes of quiet work time followed by whole-class discussion.
Design Principle(s): Maximize meta-awareness; Support sense-making
Student Facing
- Kiran was running around the track. The graph shows the time, \(t\), he took to run various distances, \(d\). The table shows his time in seconds after every three meters.
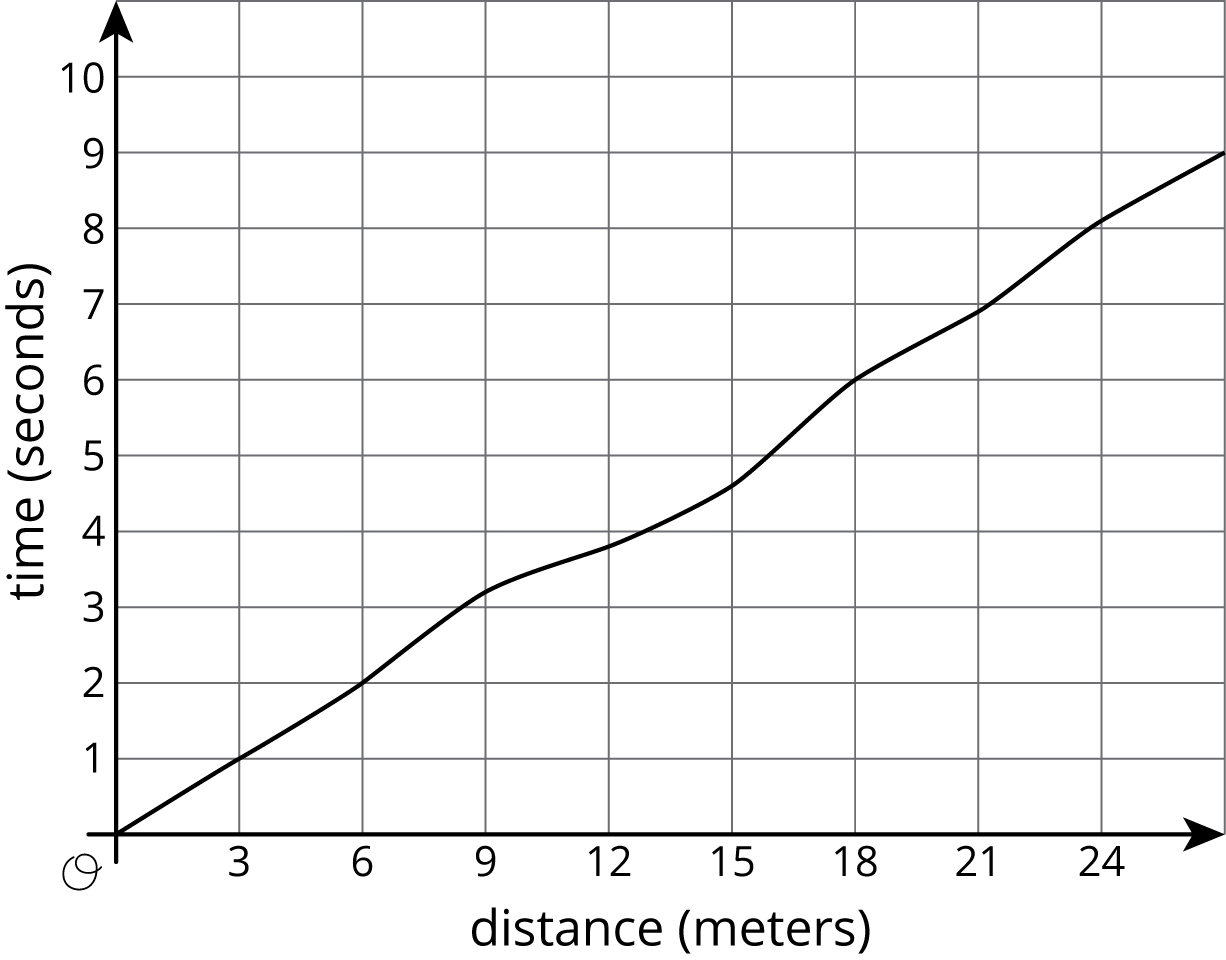
\(d\) 0 3 6 9 12 15 18 21 24 27 \(t\) 0 1.0 2.0 3.2 3.8 4.6 6.0 6.9 8.09 9.0 - How long did it take Kiran to run 6 meters?
- How far had he gone after 6 seconds?
- Estimate when he had run 19.5 meters.
- Estimate how far he ran in 4 seconds.
- Is Kiran's time a function of the distance he has run? Explain how you know.
-
Priya is running once around the track. The graph shows her time given how far she is from her starting point.

- What was her farthest distance from her starting point?
- Estimate how long it took her to run around the track.
- Estimate when she was 100 meters from her starting point.
- Estimate how far she was from the starting line after 60 seconds.
- Is Priya's time a function of her distance from her starting point? Explain how you know.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
The purpose of this discussion is for students to understand that independent and dependent variables are not determined by the context (and specifically that time is not always a function of distance). Select students to share their strategies for calculating the answers for the first set of problems. For each problem, ask students whether the graph or table was more useful. Further the discussion by asking:
- “When are tables useful for answering questions?” (The exact answers that are listed in table while with the graph we can only approximate.)
- “When are graphs more useful for answering questions?” (A graph shows more input-output pairs than a table can list easily.)
- “Why does it make sense to have time be a function of distance in this problem?” (The farther Kiran runs, the longer it will take so it makes sense to represent time as a function of distance.)
- “Does time always have to be a function of distance?” (No, this graph could be made the other way with time on the horizontal and distance on the vertical and then it would show distance as a function of time, which makes sense since the longer Kiran runs, the further he will travel.)
For the second graph, ask students to indicate if they think it represents a function or not. If there are students who say yes and no, invite students from each side to say why they think it is or is not a function and try to persuade the rest of the class to their side. If all students are not persuaded that the graph is not a function, remind students that functions can only have one output for each input, and ask students to look back at their answer to the question “Estimate when she was 100 meters from her starting point.” Since that question has two responses, the graph cannot be a function.
It time allows, ask students “If the axes of the second graph were switched, that is, time was the independent variable and distance from the starting line was the dependent variable, then would the graph be a representation of a function?” (Yes, because each input (time) would have only one output (distance).)
Supports accessibility for: Language; Social-emotional skills; Attention
Lesson Synthesis
Lesson Synthesis
Each representation of a function presents information about the input and output of the function in different ways. Tell students to imagine we have a function with independent variable \(x\) and dependent variable \(y\).
- “How do we find input-output pairs from a graph of the function?” (Any coordinate on the graph gives an input-output pair where the input is the \(x\)-value and the output is the \(y\)-value.)
- “What is something you won’t see on the graph of the function?” (The graph will never “double-back” or have two \(y\)-values for the same \(x\)-value, because each input will have only one output.)
- “If the graph of the function contains the point \((18, 6)\), what else do we know about the function?” (If we input 18 into the function we will get 6 as an output. An equation for the function could by \(y=\frac13 x\), but we would need to know more points on the graph to be sure.)
4.4: Cool-down - Subway Fare Card (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
Here is the graph showing Noah's run.
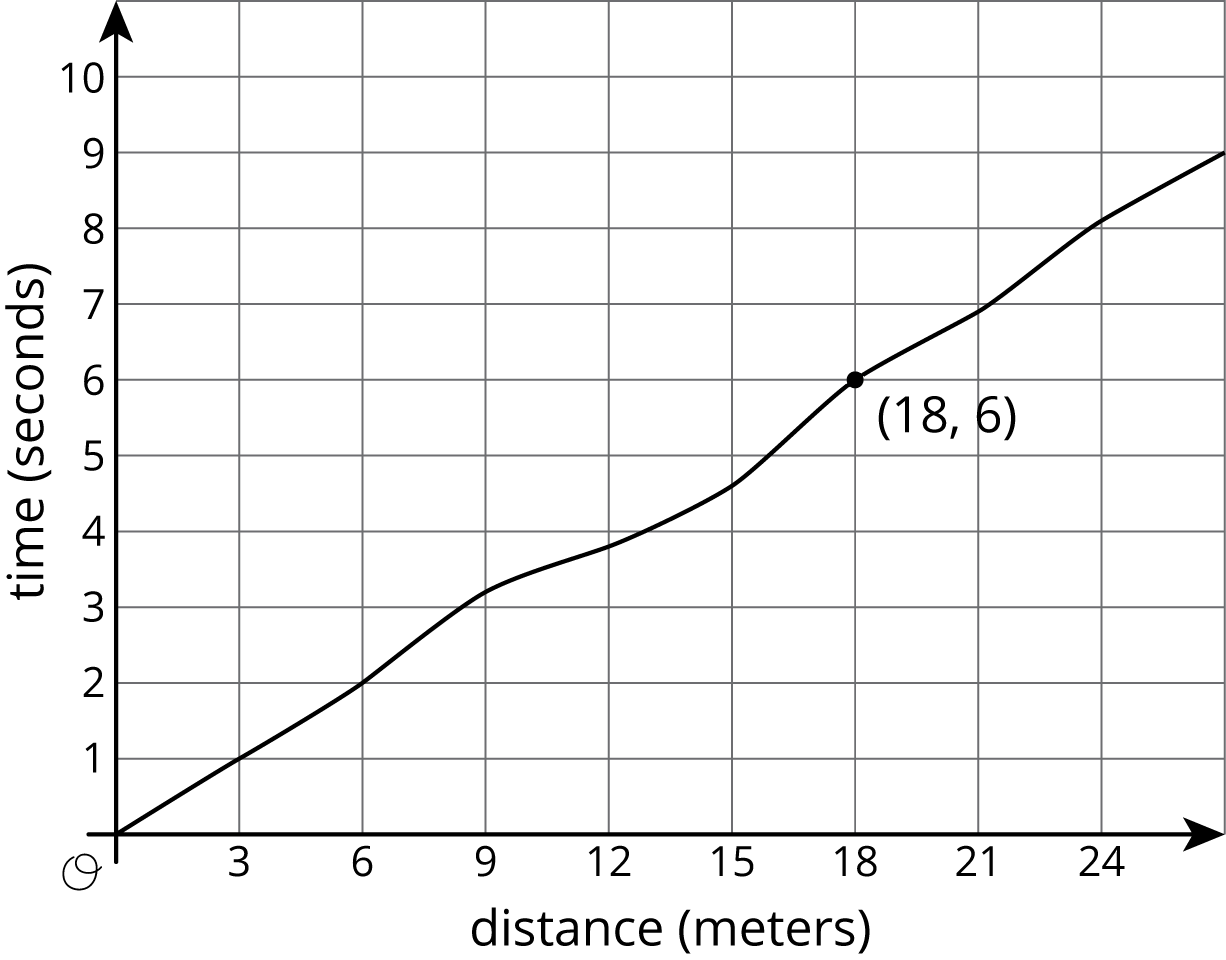
The time in seconds since he started running is a function of the distance he has run. The point (18,6) on the graph tells you that the time it takes him to run 18 meters is 6 seconds. The input is 18 and the output is 6.
The graph of a function is all the coordinate pairs, (input, output), plotted in the coordinate plane. By convention, we always put the input first, which means that the inputs are represented on the horizontal axis and the outputs, on the vertical axis.