Lesson 16
Surface Area of Right Prisms
16.1: Multifaceted (5 minutes)
Warm-up
The purpose of this warm-up is for students to recognize important parts of solids in anticipation of computing volume and surface area. The figure used in the next activity is introduced in this warm-up as a way for students to start thinking about parts of solids and how we use them to compute surface area or volume.
Launch
Arrange students in groups of 2. Display the prism assembled from the blackline master for all to see. Give students 1 minute of quiet think time followed by time to discuss their ideas with a partner. Follow with a whole-class discussion.
Student Facing
Your teacher will show you a prism.
- What are some things you could measure about the object?
-
What units would you use for these measurements?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Select students to share their responses. Ask students to think about units that do not make sense to use for measurements (feet, miles, yards, etc). Invite students to share their explanations of why these units do not make sense to use.
16.2: So Many Faces (15 minutes)
Activity
In this activity, students make sense of three different methods for calculating the surface area of a figure. Three different methods are described to students and they are asked to determine which one they agree with (if any) (MP3). They then think about generalizing the methods to figure out if they would work for any prism. This activity connects to work they did with nets in a previous grade and builds upon strategies students might have to calculate surface area.
As students work on the task, monitor for students who understand the different methods and can explain if any of them will work for any other prisms.
Note: It is not important for students to learn the term “lateral area.”
Launch
Arrange students in groups of 2. Display the prism assembled previously in the warm-up for all to see. Ask students: “how might we find surface area of this prism?” Invite students to share their ideas. Give students 1 minute of quiet think to read Noah’s method for calculating surface area followed by time discuss whether they agree with Noah or not. Repeat this process for the remaining two methods. Once all three methods have been discussed give students 1–2 minutes of quiet work time to answer the rest of the questions in the task statement.
Supports accessibility for: Visual-spatial processing
Student Facing
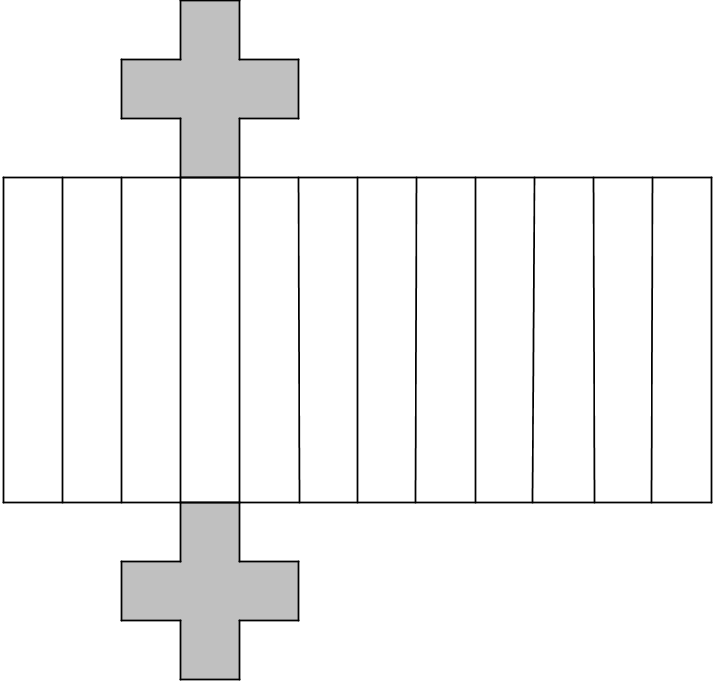
Here is a picture of your teacher's prism:

Three students are trying to calculate the surface area of this prism.
- Noah says, “This is going to be a lot of work. We have to find the areas of 14 different faces and add them up.”
- Elena says, “It’s not so bad. All 12 rectangles are identical copies, so we can find the area for one of them, multiply that by 12 and then add on the areas of the 2 bases.”
- Andre says, “Wait, I see another way! Imagine unfolding the prism into a net. We can use 1 large rectangle instead of 12 smaller ones.”
-
Do you agree with any of them? Explain your reasoning.
- How big is the “1 large rectangle” Andre is talking about? Explain or show your reasoning. If you get stuck, consider drawing a net for the prism.
- Will Noah’s method always work for finding the surface area of any prism? Elena’s method? Andre’s method? Be prepared to explain your reasoning.
-
Which method do you prefer? Why?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may think that Andre’s method will not work for all prisms, because it will not work for solids that have a hole in their base and therefore more lateral area on the inside. Technically, these solids are not prisms, because their base is not a polygon. However, students could adapt Andre’s method to find the surface area of a solid composed of a prism and a hole.
Activity Synthesis
Select previously identified students to share their reasoning. If not brought up in students' explanations, display the image for all to see and point out to students that the length of the “1 big rectangle” is equal to the perimeter of the base.
Students may have trouble generalizing which method would work for any prism. Here are some guiding questions:
- “Which of the students’ methods will work for finding the surface area of this particular prism?” (all 3)
- “Which of the students’ methods will work for finding the surface area of any prism?” (Noah’s and Andre’s)
- “Which of the students’ methods will work for finding the surface area of other three-dimensional figures that are not prisms?” (only Noah’s)
If not mentioned by students, be sure students understand:
- Noah’s method will always work, but it can be inefficient if there are a lot of faces.
- Elena’s method will not always work because the rectangles will not always be the same size, but we can notice that some shapes are the same and not have to work them all out individually.
- Andre’s method does always work even if the rectangles have different widths. The length of the rectangle will be the same as the perimeter of the base and the width of the rectangle will be the height of the prism.
- Prisms can always be cut into three pieces: two bases and one rectangle whose length is the perimeter of a base and whose width is the height of the prism. This can be more efficient than the other methods because students only need to calculate two areas (since the two bases will be identical copies).
- This method only works for prisms. For other shapes, such as pyramids, Noah’s method of finding all the faces individually or Elena’s method of combining those faces into identical copy groups will work. Solids with holes, such as the triangular prism with a square hole, can use a variation on Elena’s method: two congruent triangles with holes for the bases, one rectangle for the outside side faces, and another rectangle for the faces forming the hole.
Explain to students that they will have the opportunity in the next activity to practice using any of these strategies.
Provide students with prompts for feedback that will help their partners strengthen their ideas and clarify their language (e.g., “Can you draw a picture to support your explanation?”, “You should expand on….”, “How does that match with Andre’s thinking?”, etc.). Invite students to go back and revise or refine their written explanation based on their peer feedback. These conversations will help students make sense of the different methods for calculating the surface area of a figure.
Design Principle(s): Cultivate conversation; Optimize output (for explanation)
16.3: Revisiting the Box of Chocolates (10 minutes)
Activity
In this activity students are presented with a prism that was used in a previous lesson to calculate volume. Here, they calculate the surface area of the prism. This provides students with the opportunity to work with complex shapes to find surface area in a given context.
Launch
Display the image for all to see throughout the activity. Tell students that they calculated the volume of this heart-shaped box in a previous lesson and today they are going to calculate a different measurement. Ask students what additional information they need to find the total amount of cardboard in the box. When students recognize that they need the lengths of the diagonal sides of the box give them the measurements for those sides (2.2 inches for the sides around the top and 6.4 inches for the sides around the bottom). Give students 2–3 minutes of quiet work time followed by a whole-class discussion.

Supports accessibility for: Memory; Conceptual processing
Student Facing
The other day, you calculated the volume of this heart-shaped box of chocolates.
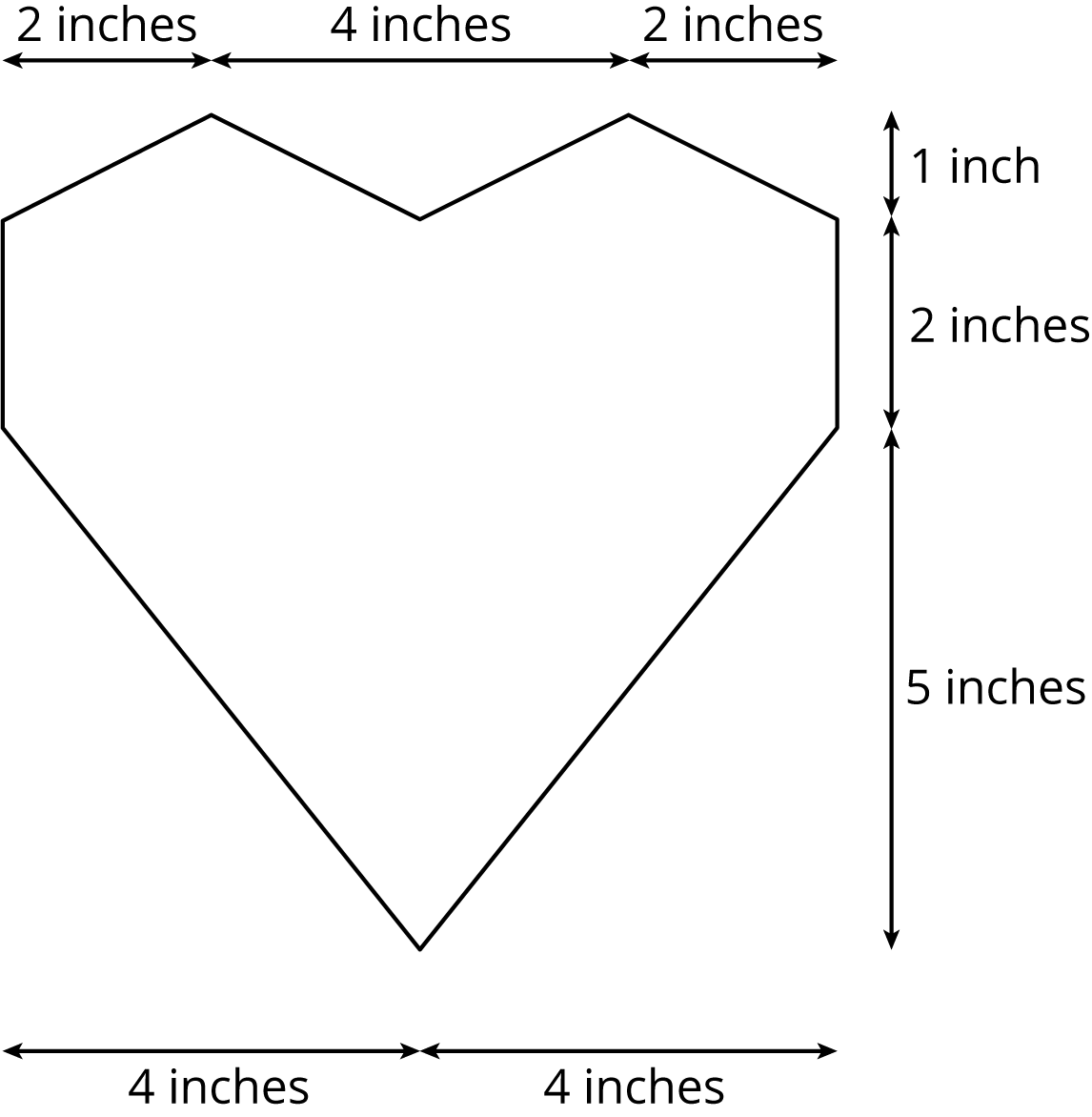
The depth of the box is 2 inches. How much cardboard is needed to create the box?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students who are familiar with actual heart-shaped boxes of chocolate may want to double the lateral area to represent the way the top and bottom pieces nest together.
Activity Synthesis
Select students to share their solutions and methods for calculating the surface area. Consider asking some of the following questions:
- “How did you figure out that you had to calculate the surface area of the box?”
- “What method did you use to calculate the surface area?”
- “If the candy maker wants to make a set of two boxes that are each half of a heart and could be put together to make a box that looks like this one, would the total amount of cardboard used to make the two boxes be different than making the one box?” (Yes, it would increase.)
- “How could the candy maker reduce the surface area of the one box without reducing the volume?” (If he made it a triangle or some other shape with fewer segments instead of a heart.)
Design Principle(s): Cultivate conversation; Maximize meta-awareness
16.4: A Wheelbarrow of Concrete (5 minutes)
Optional activity
This optional activity reinforces work students have done in previous activities with regards to surface area and volume. Students work with a contextual problem to determine the surface area and volume of an object.
Launch
Arrange students in groups of 2. If desired, display the image of a wheelbarrow for all to see.

Give students 1–2 minutes of quiet work time followed by time to discuss their answers with their partner. Follow with a whole-class discussion.
Student Facing
A wheelbarrow is being used to carry wet concrete. Here are its dimensions.
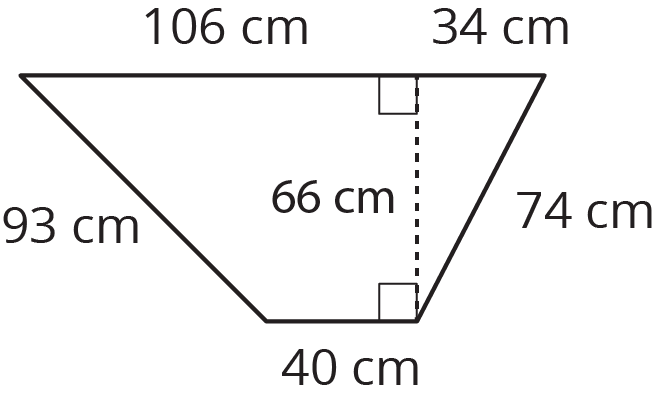
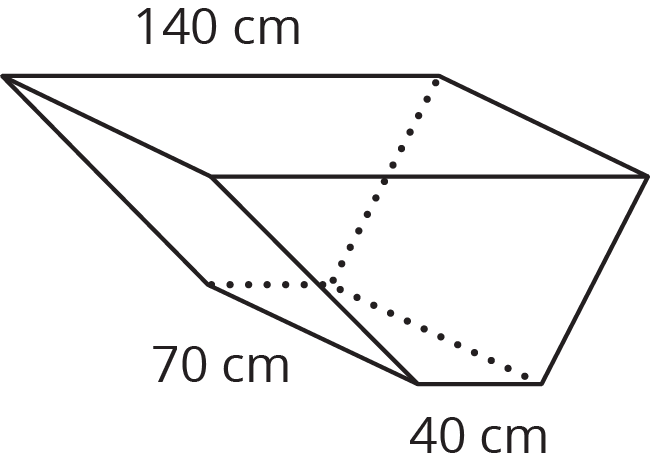
- What volume of concrete would it take to fill the tray?
-
After dumping the wet concrete, you notice that a thin film is left on the inside of the tray. What is the area of the concrete coating the tray? (Remember, there is no top.)
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Reveal the solution to each problem and give students a few minutes to resolve any discrepancies with their partners.
Design Principle(s): Optimize output (for explanation); Cultivate conversation
Lesson Synthesis
Lesson Synthesis
- “What is surface area?” (The total area of all the exposed faces of an object.)
- “What are some methods for calculating surface area of prisms?” (Find the area of each face and add them for the total. Find groups of faces that have the same area and save some computation. Find the area of the bases and add that to the area of a “long rectangle.”)
- “When is it better to know surface area than volume?” (when you are covering an object, when you want to know how much is exposed to the environment, or other examples involving only the exterior of an object.)
- “When is it better to know volume than surface area?” (when you are filling up the object, when you need to know how much is already inside, or other examples in which the interior of the object is needed.)
16.5: Cool-down - Surface Area of a Hexagonal Prism (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
To find the surface area of a three-dimensional figure whose faces are made up of polygons, we can find the area of each face, and add them up!
Sometimes there are ways to simplify our work. For example, all the faces of a cube with side length \(s\) are the same. We can find the area of one face, and multiply by 6. Since the area of one face of a cube is \(s^2\), the surface area of a cube is \(6s^2\).
We can use this technique to make it faster to find the surface area of any figure that has faces that are the same.
For prisms, there is another way. We can treat the prism as having three parts: two identical bases, and one long rectangle that has been taped along the edges of the bases. The rectangle has the same height as the prism, and its width is the perimeter of the base. To find the surface area, add the area of this rectangle to the areas of the two bases.
When working with prisms, sometimes we need to find the volume and sometimes we need to find the surface area.
Here are some examples of quantities related to volume:
- How much water a container can hold
- How much material it took to build a solid object
Volume is measured in cubic units, like in3 or m3.
Here are some examples of quantities related to surface area:
- How much fabric is needed to cover a surface
- How much of an object needs to be painted
Surface area is measured in square units, like in2 or m2.