Lesson 14

Using Diagrams to Represent Addition and Subtraction

Let’s represent addition and subtraction of decimals.

Problem 1

Here are diagrams that represent 0.137 and 0.284.

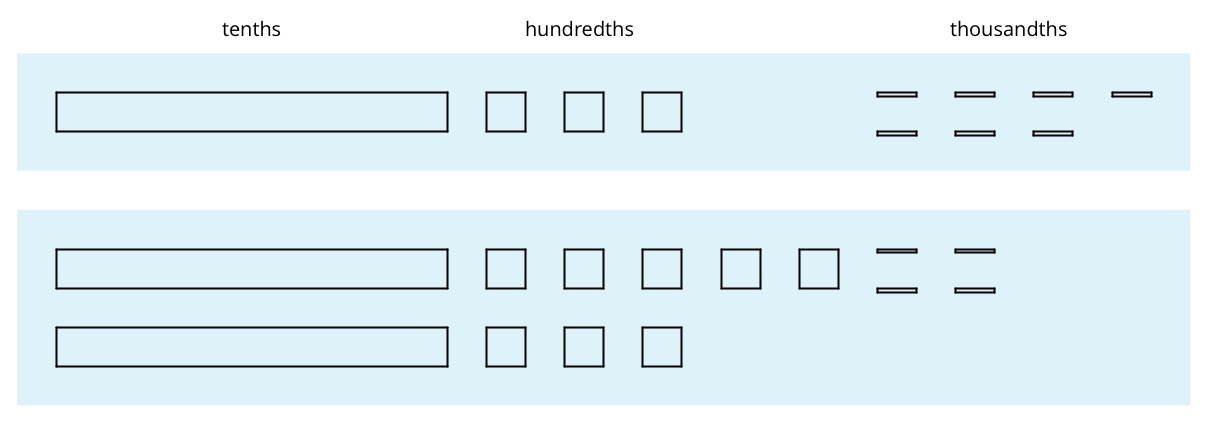
Two base-ten diagrams representing 0 point 1 3 7 and 0 point 2 8 4.
  1. Use the diagram to find the value of \(0.137 + 0.284\). Explain your reasoning.

  2. Calculate the sum vertically.

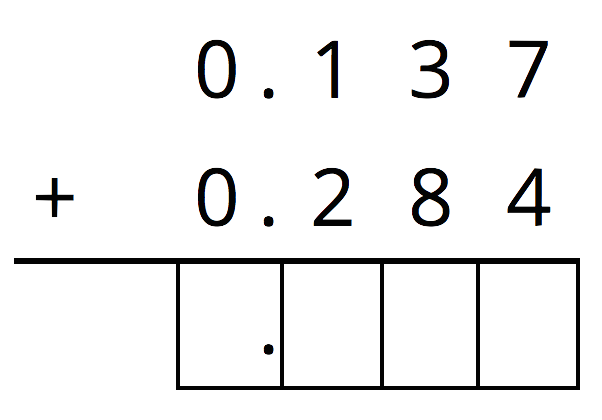
    Calculation with missing digits. 0 point 1 3 7 plus 0 point 2 8 4 is equal to an unknown quantity with four digits.

  3. How was your reasoning about \(0.137 + 0.284\) the same with the two methods? How was it different?

Problem 2

For the first two problems, circle the vertical calculation where digits of the same kind are lined up. Then, finish the calculation and find the sum. For the last two problems, find the sum using vertical calculation.

  1. \(3.25+1\)

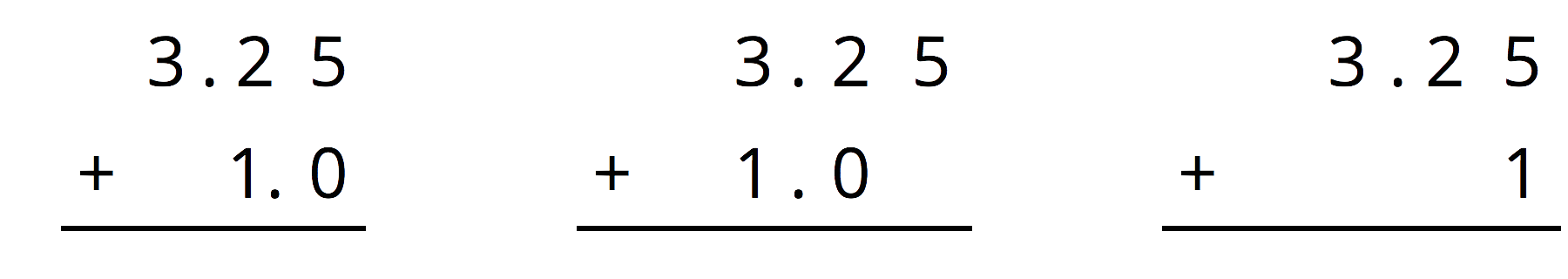
    3 vertical calculations of 3 point 2 5 plus 1.

  2. \(0.5+1.15\)

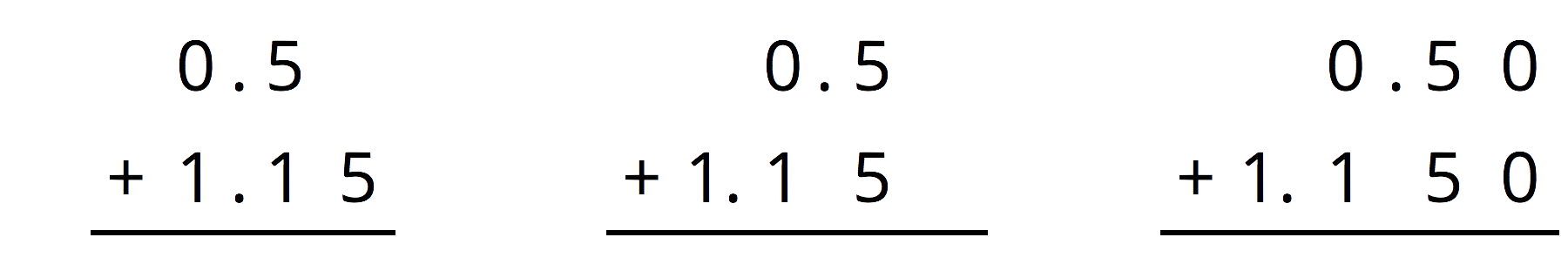
    3 vertical calculations of 0 point 5 plus 1 point 1 5.

  3. \(10.6+ 1.7\)

  4. \(123+0.2\)

Problem 3

Here is a base-ten diagram that represents 1.13. Use the diagram to find \(1.13 - 0.46\).

Explain or show your reasoning.

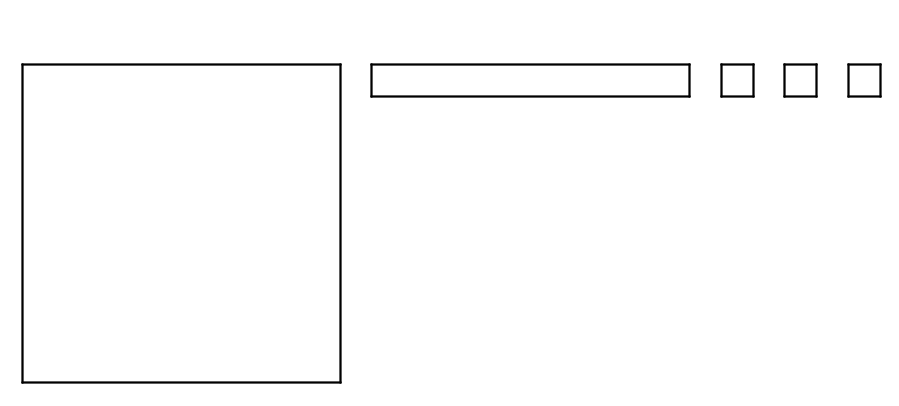
A base-ten diagram representing 1 point 1 3. 1 large square, 1 rectangle, and 3 small squares. 

 

(From Unit 3, Lesson 15.)

Problem 4

Complete the calculations so that each shows the correct difference.

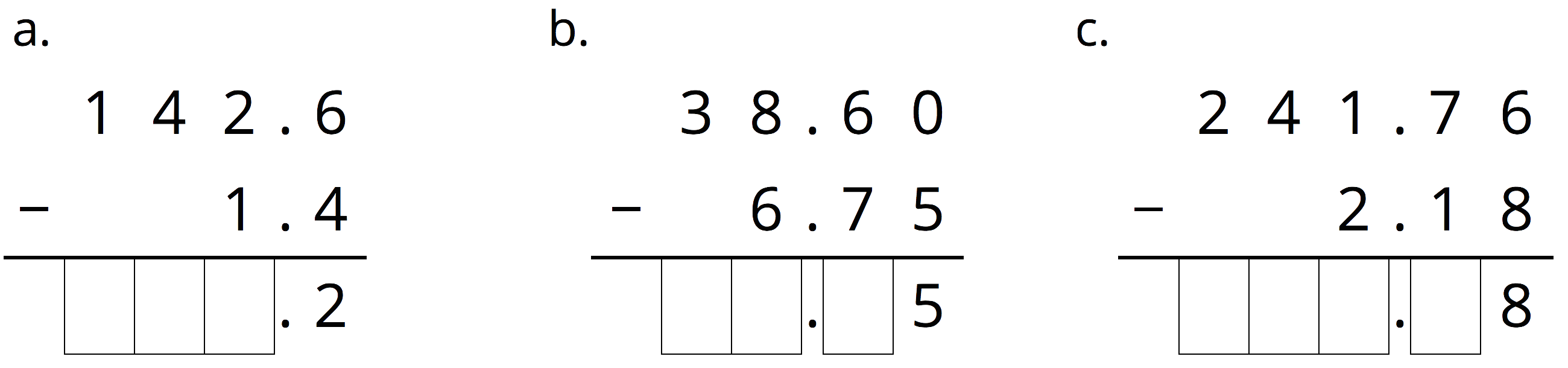
3 decimal subtraction problems. 

 

Problem 5

A rectangular prism measures \(7\frac{1}{2}\) cm by 12 cm by \(15\frac{1}{2}\) cm.

  1. Calculate the number of cubes with edge length \(\frac{1}{2}\) cm that fit in this prism.
  2. What is the volume of the prism in \(\text{cm}^3\)? Show your reasoning. If you are stuck, think about how many cubes with \(\frac12\)-cm edge lengths fit into \(1\text{ cm}^3\).
(From Unit 3, Lesson 11.)

Problem 6

At a constant speed, a car travels 75 miles in 60 minutes. How far does the car travel in 18 minutes? If you get stuck, consider using the table.

minutes distance in miles
60 75
6
18
(From Unit 2, Lesson 9.)