Lesson 4

1. Estimate the quantities:

   1. What is \(\frac13\) of 7?
   2. What is \(\frac45\) of \(9\frac23\)?
   3. What is \(2\frac47\) of \(10\frac19\)?
2. Write a multiplication expression for each of the previous questions.

The segments in the applet represent 4 different lengths of rope. Compare one rope to another, moving the rope by dragging the open circle at one endpoint. You can use the yellow pins to mark off lengths.

1. Complete each sentence comparing the lengths of the ropes. Then, use the measurements shown on the grid to write a multiplication equation and a division equation for each comparison.
   1. Rope B is _______ times as long as rope A.
   2. Rope C is _______ times as long as rope A.
   3. Rope D is _______ times as long as rope A.

2. Each equation can be used to answer a question about Ropes C and D. What could each question be?

   1. \({?} \boldcdot 3=9\) and \(9 \div 3={?}\)

   2. \({?} \boldcdot 9=3\) and \(3 \div 9= {?}\)

One batch of an ice cream recipe uses 9 cups of milk. A chef makes different amounts of ice cream on different days. Here are the amounts of milk she used:

1. How many batches of ice cream did she make on these days? For each day, write a division equation, draw a tape diagram, and find the answer.

   1. Monday

      

      

   2. Tuesday

      

      

2. What fraction of a batch of ice cream did she make on these days? For each day, write a division equation, draw a tape diagram, and find the answer.

   1. Thursday

      

      

   2. Friday

      

      

3. For each question, write a division equation, draw a tape diagram, and find the answer.

   1. What fraction of 9 is 3?

      

      

   2. What fraction of 5 is \(\frac 12\)?

      

      

It is natural to think about groups when we have more than one group, but we can also have a fraction of a group.

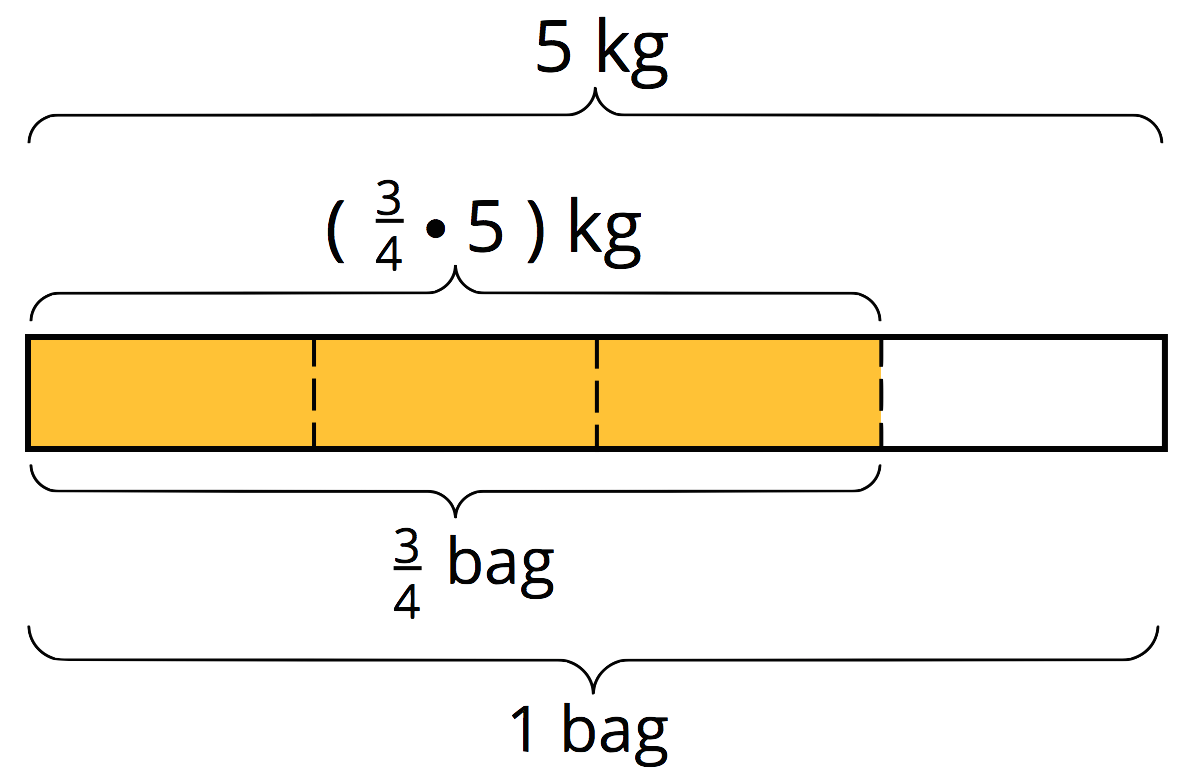
To find the amount in a fraction of a group, we can multiply the fraction by the amount in the whole group. If a bag of rice weighs 5 kg, \(\frac34\) of a bag would weigh (\(\frac34 \boldcdot 5)\) kg.

Sometimes we need to find what fraction of a group an amount is. Suppose a full bag of flour weighs 6 kg. A chef used 3 kg of flour. What fraction of a full bag was used? In other words, what fraction of 6 kg is 3 kg?

This question can be represented by a multiplication equation and a division equation, as well as by a diagram.

\(\displaystyle {?} \boldcdot 6 = 3\) \(\displaystyle 3\div 6 = {?}\)

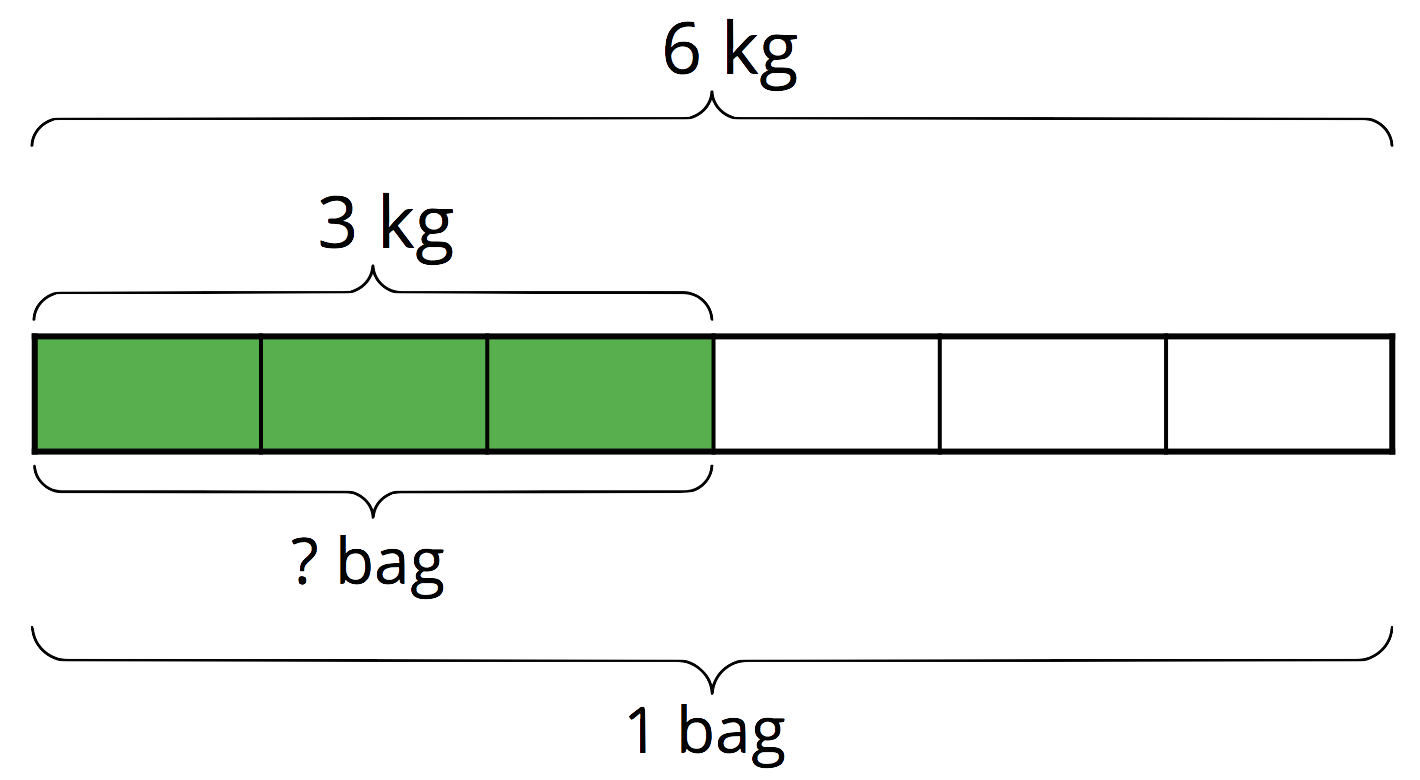
We can see from the diagram that 3 is \(\frac12\) of 6, and we can check this answer by multiplying: \(\frac12 \boldcdot 6 = 3\).

In any situation where we want to know what fraction one number is of another number, we can write a division equation to help us find the answer.

For example, “What fraction of 3 is \(2\frac14\)?” can be expressed as \({?} \boldcdot 3 = 2\frac14\), which can also be written as \(2\frac14\div 3 = {?}\).

The answer to “What is \(2\frac14 \div 3\)?” is also the answer to the original question.

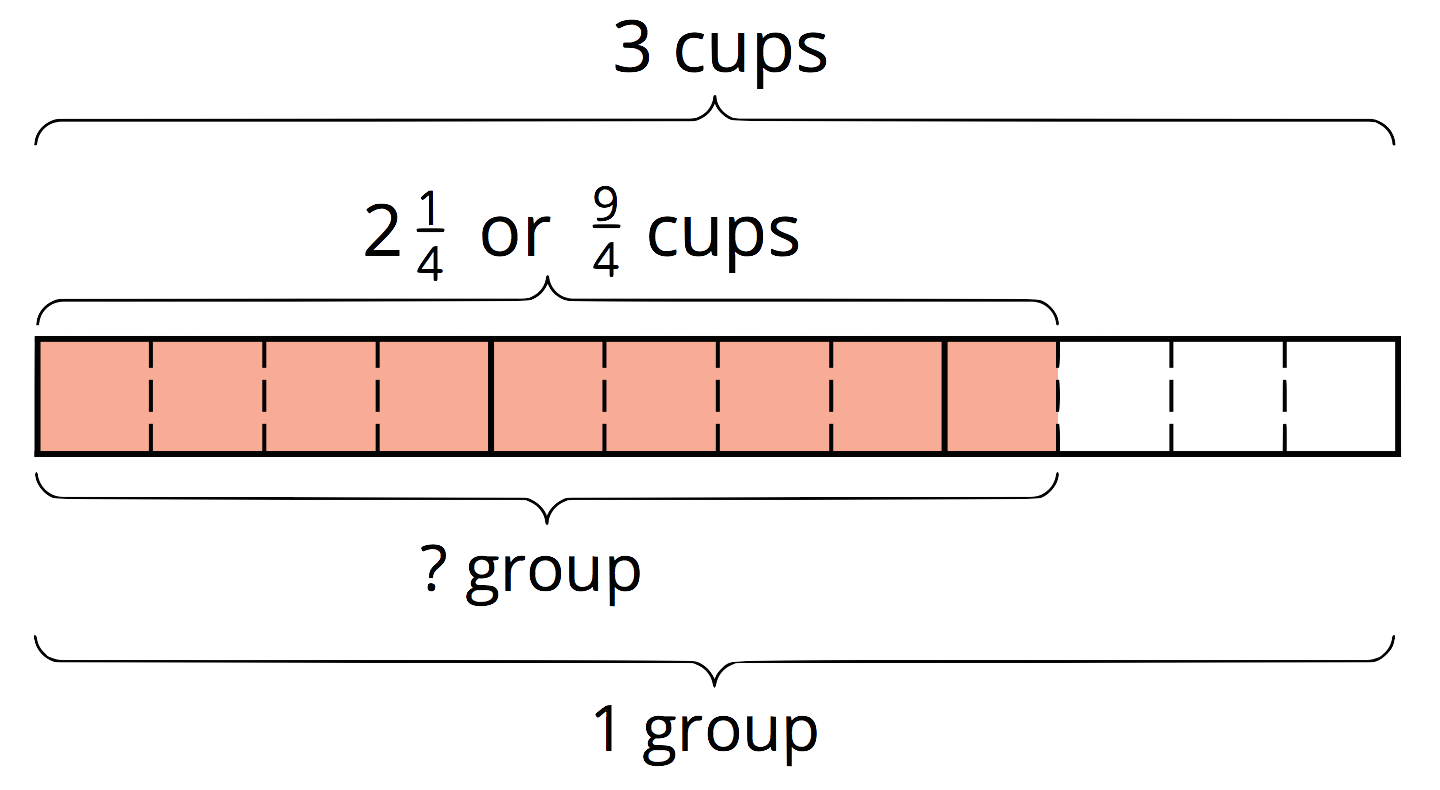
The diagram shows that 3 wholes contain 12 fourths, and \(2\frac14\) contains 9 fourths, so the answer to this question is \(\frac{9}{12}\), which is equivalent to \(\frac34\).

We can use diagrams to help us solve other division problems that require finding a fraction of a group. For example, here is a diagram to help us answer the question: “What fraction of \(\frac94\) is \(\frac32\)?,” which can be written as \(\frac32 \div \frac94 = {?}\).

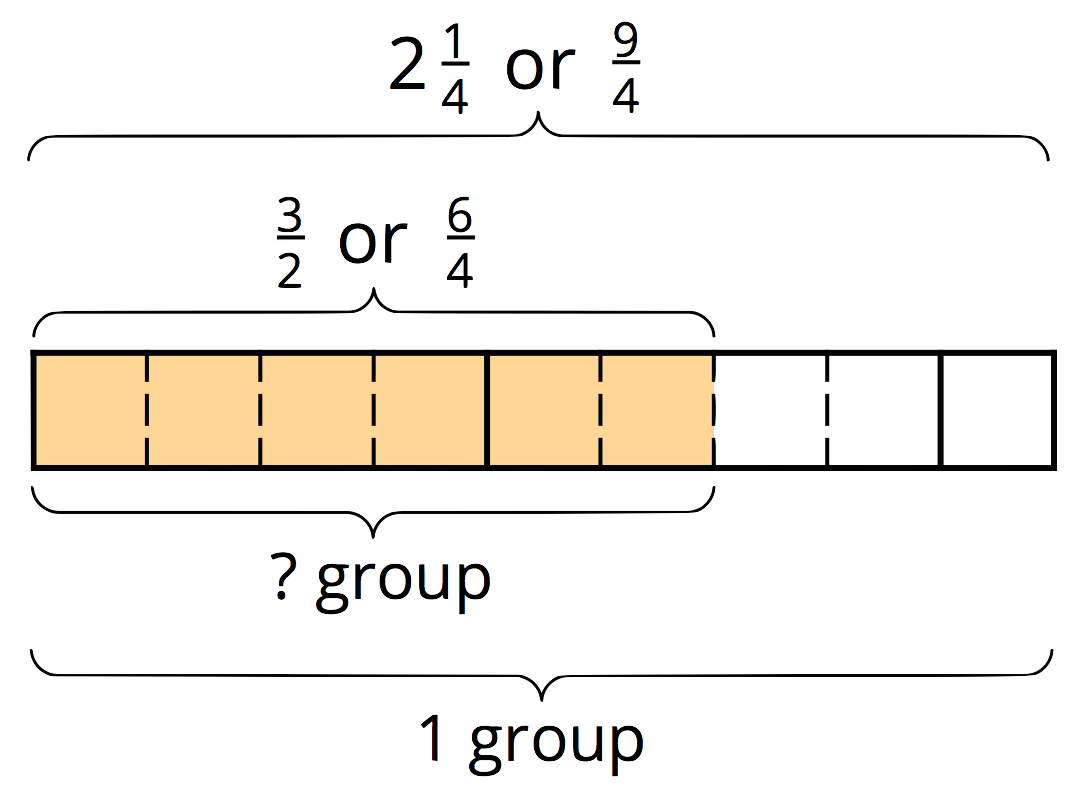
We can see that the quotient is \(\frac69\), which is equivalent to \(\frac23\). To check this, let’s multiply. \(\frac23 \boldcdot \frac94 = \frac{18}{12}\), and \(\frac{18}{12}\) is, indeed, equal to \(\frac32\).