Lesson 7

Evaluate each expression.

1. \(\frac 23 \boldcdot 27\)
2. \(\frac 12 \boldcdot \frac 23\)
3. \(\frac 29 \boldcdot \frac 35\)
4. \(\frac {27}{100} \boldcdot \frac {200}{9}\)
5. \(\left( 1\frac 34 \right) \boldcdot \frac 57\)

1. To find the value of \(6 \div \frac 23\), Elena started by drawing a diagram the same way she did for \(6 \div \frac 13\).

   

   

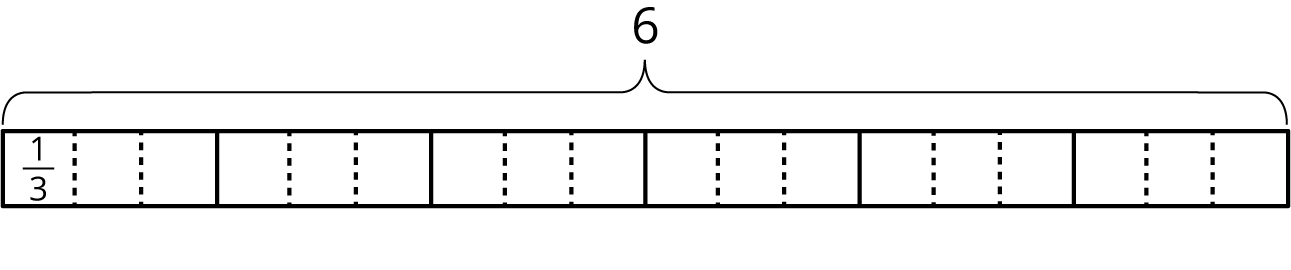
   1. Complete the diagram to show how many \(\frac 23\)s are in 6.
   2. Elena says, “To find \(6 \div \frac23\), I can just take the value of \(6 \div \frac13\) and then either multiply it by \(\frac 12\) or divide it by 2.” Do you agree with her? Explain your reasoning.

2. For each division expression, complete the diagram using the same method as Elena. Then, find the value of the expression. Think about how you could find that value without counting all the pieces in your diagram.

   1. 
      \(6 \div \frac 34\)

      

      

      Value of the expression:___________

   2. ​​​​​​
      \(6 \div \frac 43\)

      

      

      Value of the expression:___________

   3. 
      \(6 \div \frac 46\)

      

      

      Value of the expression:___________

3. Elena examined her diagrams and noticed that she always took the same two steps to show division by a fraction on a tape diagram. She said:

   “My first step was to divide each 1 whole into as many parts as the number in the denominator. So if the expression is \(6 \div \frac 34\), I would break each 1 whole into 4 parts. Now I have 4 times as many parts.

   My second step was to put a certain number of those parts into one group, and that number is the numerator of the divisor. So if the fraction is \(\frac34\), I would put 3 of the \(\frac 14\)s into one group. Then I could tell how many \(\frac 34\)s are in 6.”

   Which expression represents how many \(\frac 34\)s Elena would have after these two steps? Be prepared to explain your reasoning.

   • \(6 \div 4 \boldcdot 3\)
   • \(6 \div 4 \div 3\)

   • \(6 \boldcdot 4 \div 3\)
   • \(6 \boldcdot 4 \boldcdot 3\)

4. Use the pattern Elena noticed to find the values of these expressions. If you get stuck, consider drawing a diagram.

   1. \(6 \div \frac27\)
   2. \(6\div\frac{3}{10}\)
   3. \(6 \div \frac {6}{25}\)

Work with a partner. One person works on the questions labeled “Partner A” and the other person works on those labeled “Partner B.”

1. Partner A:

   Find the value of each expression by completing the diagram.

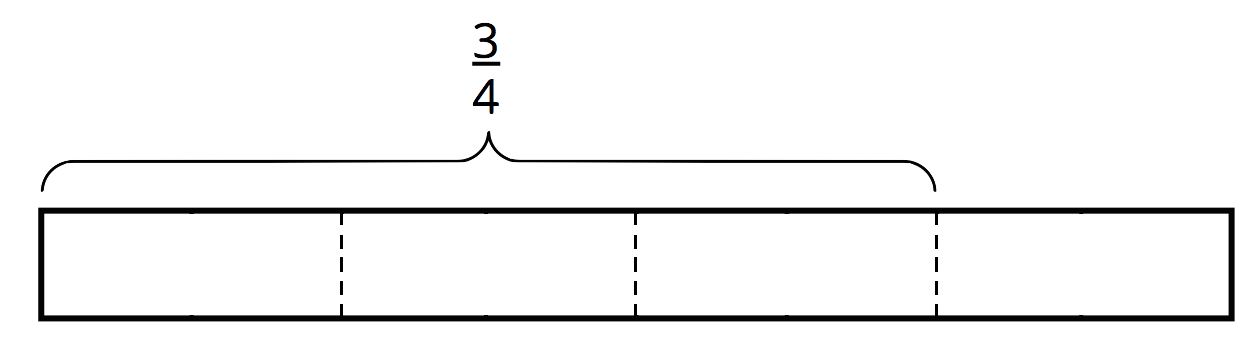
   1. \(\frac 34 \div \frac 18\)

      How many \(\frac 18\)s in \(\frac 34\)?

      

      

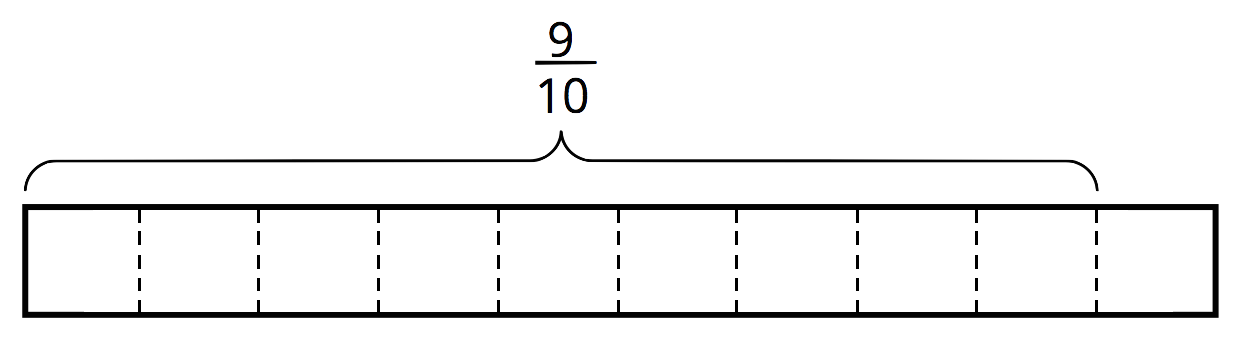
   2. \(\frac {9}{10} \div \frac 35\)

      How many \(\frac 35\)s in \(\frac{9}{10}\)?

      

      

   Use the applet to confirm your answers and explore your own examples.

   Partner B:

   Elena said: “If I want to divide 4 by \(\frac 25\), I can multiply 4 by 5 and then divide it by 2 or multiply it by \(\frac 12\).”

   Find the value of each expression using the strategy Elena described.

   1. \(\frac 34 \div \frac 18\)
   2. \(\frac{9}{10} \div \frac35\)

2. What do you notice about the diagrams and expressions? Discuss with your partner.

3. Complete this sentence based on what you noticed:

   To divide a number \(n\) by a fraction \(\frac {a}{b}\), we can multiply \(n\) by ________ and then divide the product by ________.

4. Select all equations that represent the statement you completed.

   • \(n \div \frac {a}{b} = n \boldcdot b \div a\)
   • \(n \div \frac {a}{b}= n \boldcdot a \div b\)

   • \(n \div \frac {a}{b} = n \boldcdot \frac {a}{b}\)
   • \(n \div \frac {a}{b} = n \boldcdot \frac {b}{a}\)

To answer the question “How many \(\frac 13\)s are in 4?” or “What is \(4 \div \frac 13\)?”, we can reason that there are 3 thirds in 1, so there are \((4\boldcdot 3)\) thirds in 4.

In other words, dividing 4 by \(\frac13\) has the same result as multiplying 4 by 3. 

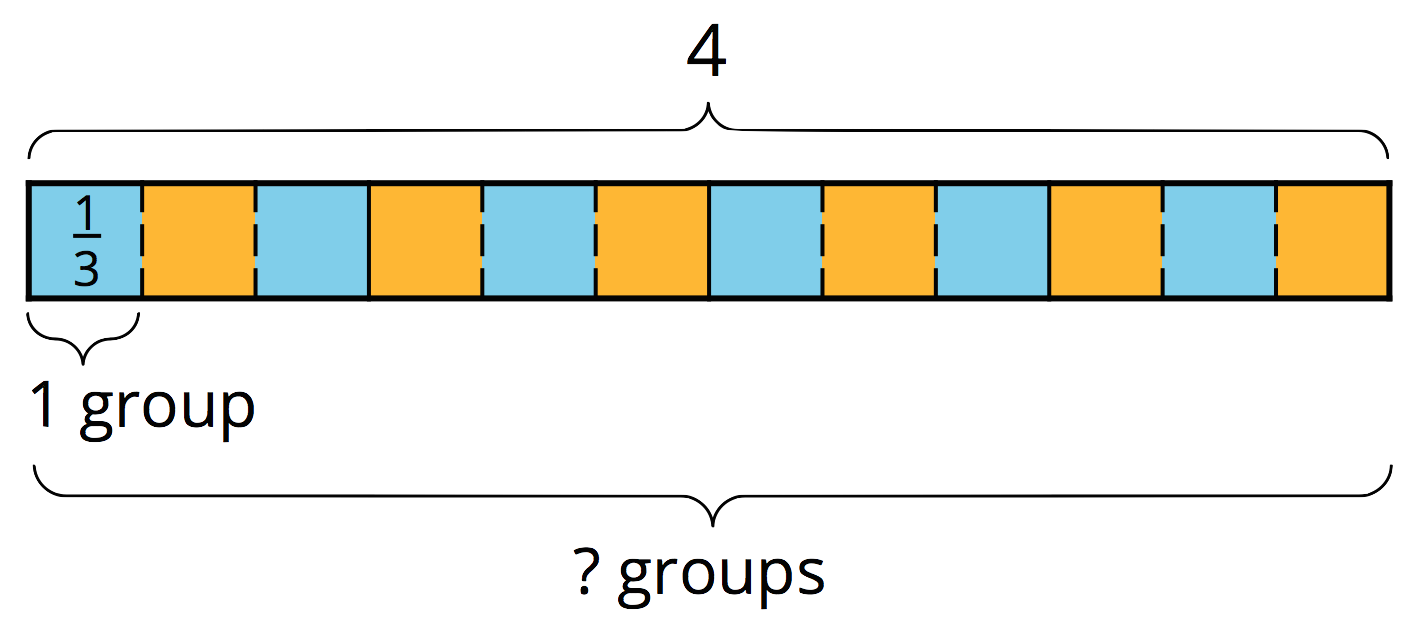
\(\displaystyle 4\div \frac13 = 4 \boldcdot 3\)

In general, dividing a number by a unit fraction \(\frac{1}{b}\) is the same as multiplying the number by \(b\), which is the reciprocal of \(\frac{1}{b}\).

How can we reason about \(4 \div \frac23\)?

We already know that there are \((4\boldcdot 3)\) or 12 groups of \(\frac 13\)s in 4. To find how many \(\frac23\)s are in 4, we need to put together every 2 of the \(\frac13\)s into a group. Doing this results in half as many groups, which is 6 groups. In other words:

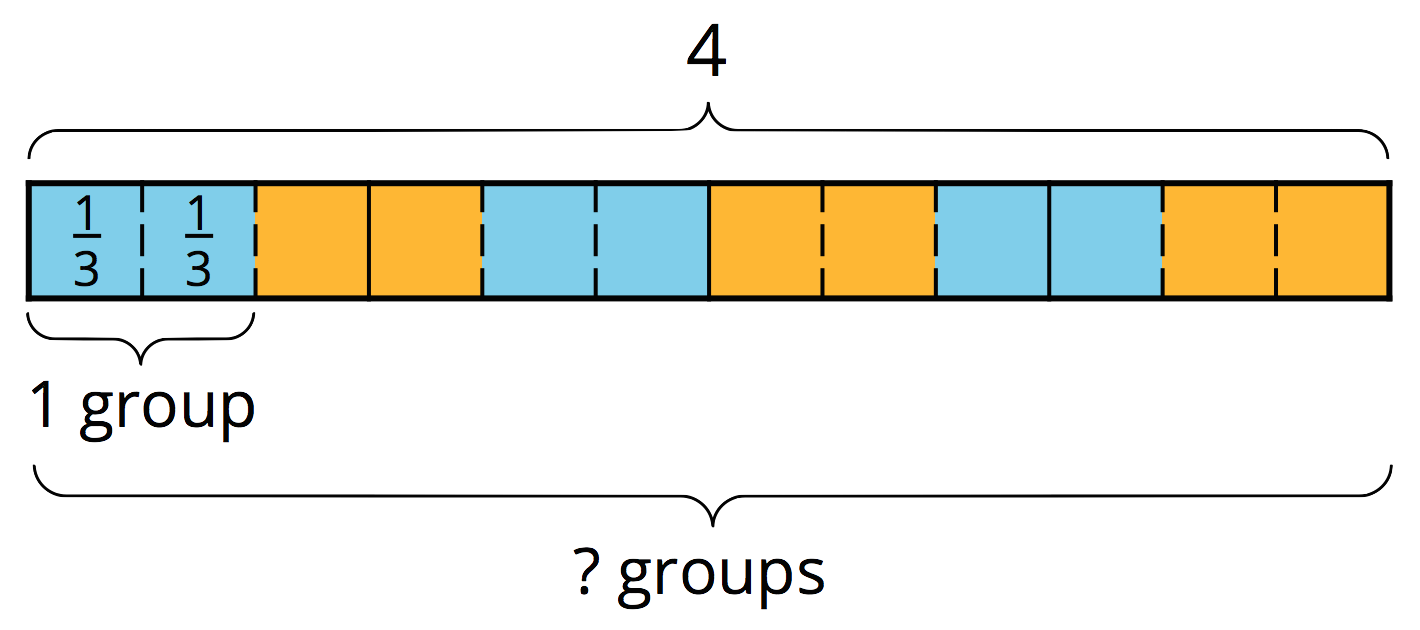
\(\displaystyle 4 \div \frac23 = (4 \boldcdot 3) \div 2\)

or

\(\displaystyle 4 \div \frac23 = (4 \boldcdot 3) \boldcdot \frac 12\)

In general, dividing a number by a fraction \(\frac{a}{b}\) is the same as multiplying the number by \(\frac{b}{a}\), which is the reciprocal of the fraction.