Lesson 6

How Much in Each Group? (Part 2)

Let’s practice dividing fractions in different situations.

6.1: Number Talk: Greater Than 1 or Less Than 1?

Decide whether each quotient is greater than 1 or less than 1.

\(\frac12\div\frac14\)

\(1\div\frac34\)

\(\frac23\div\frac78\)

\(2\frac78\div2\frac35\)

6.2: Two Water Containers

Three images. First, a measuring cup filled with the fraction 3 over 4 liters of water. Second, water in measuring cup being poured into a water dispenser with five equal spaced tick marks. Third, water up to the second tick mark on dispenser.  
  1. After looking at these pictures, Lin says, “I see the fraction \(\frac 25\).” Jada says, “I see the fraction \(\frac 34\).” What quantities are Lin and Jada referring to?

  2. Consider the problem: How many liters of water fit in the water dispenser?

    1. Write a multiplication equation and a division equation for the question.

    2. Find the answer and explain your reasoning. If you get stuck, consider drawing a diagram.

    3. Check your answer using the multiplication equation.

6.3: Amount in One Group

Write a multiplication equation and a division equation and draw a diagram to represent each situation. Then, find the answer and explain your reasoning.

  1. Jada bought \(3\frac12\) yards of fabric for $21. How much did each yard cost?

  2. \(\frac 49\) kilogram of baking soda costs $2. How much does 1 kilogram of baking soda cost?

  3. Diego can fill \(1\frac15\) bottles with 3 liters of water. How many liters of water fill 1 bottle?

  4. \(\frac54\) gallons of water fill \(\frac56\) of a bucket. How many gallons of water fill the entire bucket?



The largest sandwich ever made weighed 5,440 pounds. If everyone on Earth shares the sandwich equally, how much would you get? What fraction of a regular sandwich does this represent?

6.4: Inventing Another Situation

  1. Think of a situation with a question that can be represented by \(\frac{1}{3}\div\frac14 = {?}\). Describe the situation and the question.

  2. Trade descriptions with a partner.

    • Review each other’s description and discuss whether each question matches the equation.
    • Revise your description based on the feedback from your partner.
  3. Find the answer to your question. Explain or show your reasoning. If you get stuck, consider drawing a diagram.

Summary

Sometimes we have to think carefully about how to solve a problem that involves multiplication and division. Diagrams and equations can help us.

For example, \(\frac34\) of a pound of rice fills \(\frac25\) of a container. There are two whole amounts to keep track of here: 1 whole pound and 1 whole container. The equations we write and the diagram we draw depend on what question we are trying to answer.

  • How many pounds fill 1 container?

    \(\displaystyle \frac 25 \boldcdot {?} = \frac 34\)

    \(\displaystyle \frac 34 \div \frac 25 = {?}\)

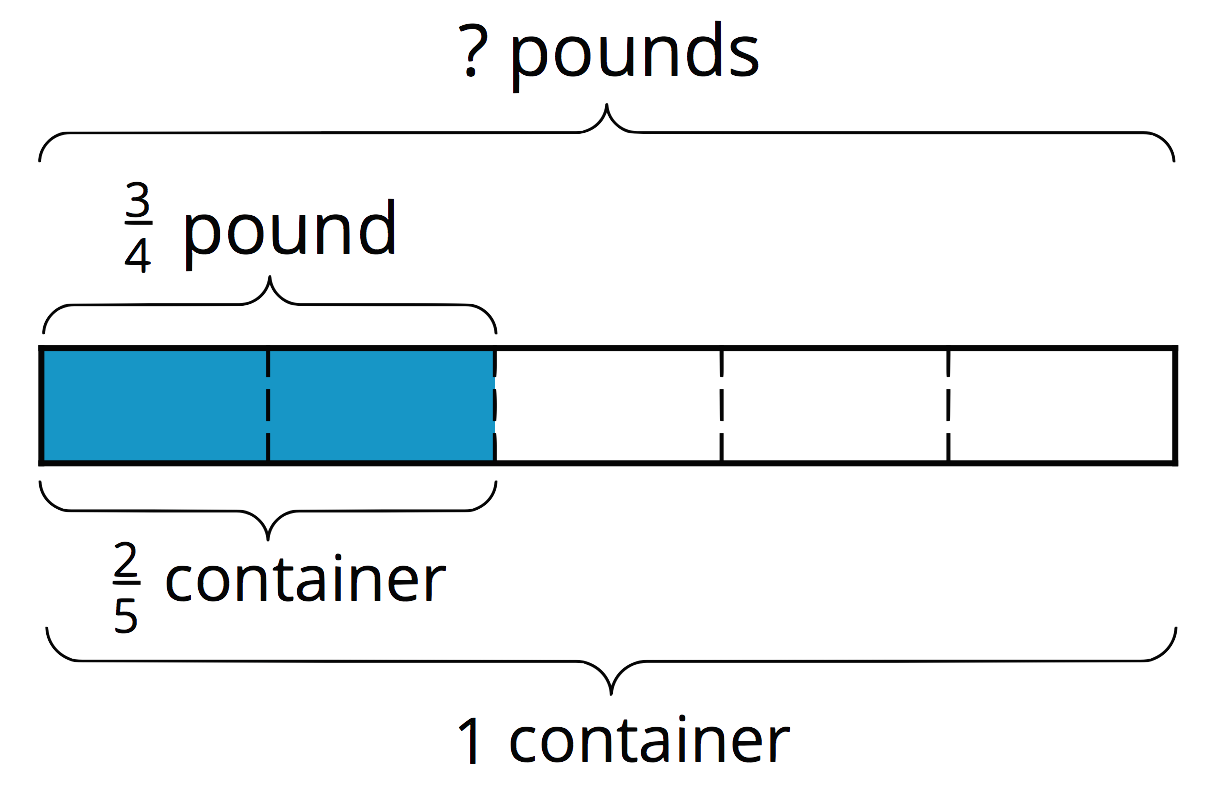
    Fraction bar diagram. 5 equal parts. 2 parts shaded.

    If \(\frac25\) of a container is filled with \(\frac 34\) pound, then \(\frac 15\) of a container is filled with half of \(\frac34\), or \(\frac38\), pound. One whole container then has \(5 \boldcdot \frac38\) (or \(\frac {15}{8}\)) pounds.

  • What fraction of a container does 1 pound fill?

    \(\displaystyle \frac34 \boldcdot {?} = \frac25\)

    \(\displaystyle \frac25 \div \frac34 ={?}\)

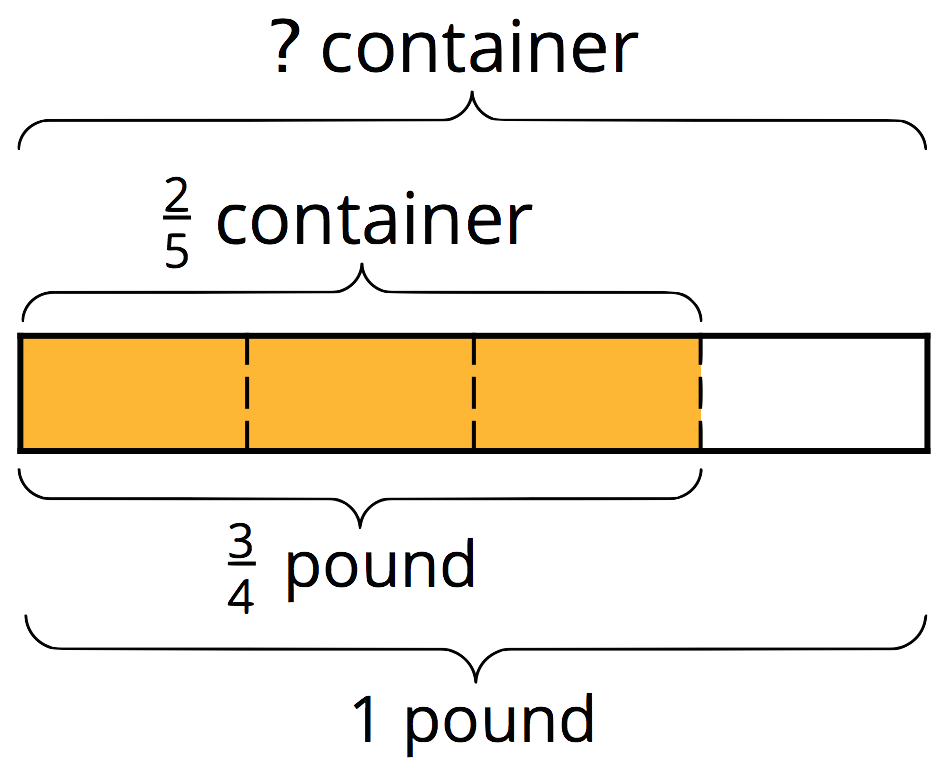
    Fraction bar diagram. 4 equal parts. 3 parts shaded. 

    If \(\frac 34\) pound fills \(\frac25\) of a container, then \(\frac14\) pound fills a third of \(\frac25\), or \(\frac {2}{15}\), of a container. One whole pound then fills \(4 \boldcdot \frac{2}{15}\) (or \(\frac {8}{15}\)) of a container.