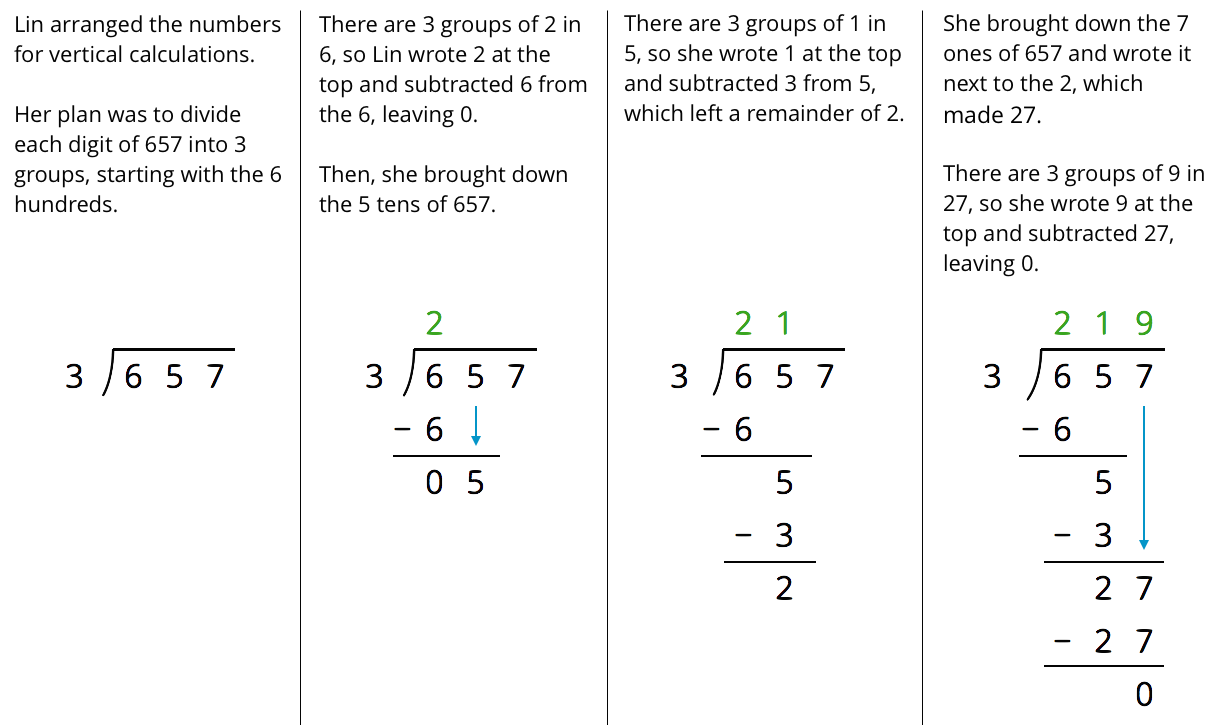
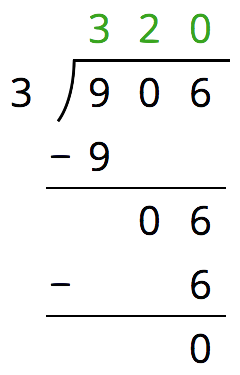Long division is an algorithm for finding the quotient of two numbers expressed in decimal form. It works by building up the quotient one digit at a time, from left to right. Each time you get a new digit, you multiply the divisor by the corresponding base ten value and subtract that from the dividend.
Using long division we see that \(513 \div 4 = 128 \frac14\). We can also write this as \(513 = 128 \times 4 + 1\).