Lesson 10

Rectangles and Triangles with Fractional Lengths

Let’s explore rectangles and triangles that have fractional measurements.

10.1: Areas of Squares

Three squares. The first square is labeled with side length 1 inch. The second square is labeled with side length one half inch. The third square is labeled with side length 2 inches.
  1. What do you notice about the areas of the squares?
  2. Kiran says “A square with side lengths of \(\frac13\) inch has an area of \(\frac13\) square inches.” Do you agree? Explain or show your reasoning.

10.2: How Many Would it Take? (Part 2)

Noah would like to cover a rectangular tray with rectangular tiles. The tray has a width of \(11\frac14\) inches and an area of \(50\frac58\) square inches.

  1. Find the length of the tray in inches.
  2. If the tiles are \(\frac{3}{4}\) inch by \(\frac{9}{16}\) inch, how many would Noah need to cover the tray completely, without gaps or overlaps? Explain or show your reasoning.
  3. Draw a diagram to show how Noah could lay the tiles. Your diagram should show how many tiles would be needed to cover the length and width of the tray, but does not need to show every tile.

10.3: Bases and Heights of Triangles

  1. Find the area of Triangle A in square centimeters. Show your reasoning.

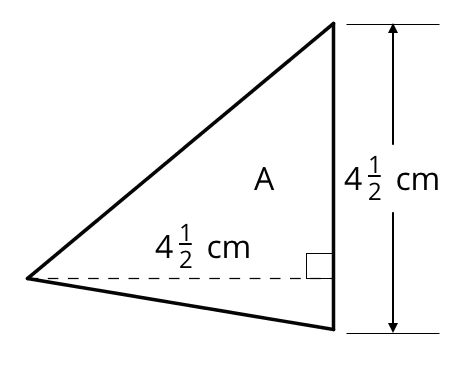
    Triangle labeled A.

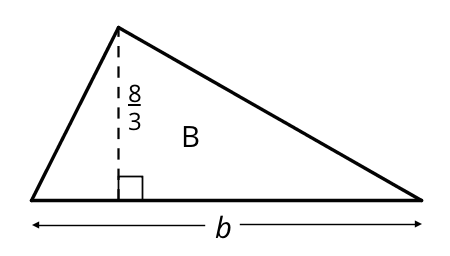
  2. The area of Triangle B is 8 square units. Find the length of \(b\). Show your reasoning.

    Triangle labeled B.. 

  3. The area of Triangle C is \(\frac{54}{5}\) square units. What is the length of \(h\)? Show your reasoning.

    Triangle labeled C.

Summary

If a rectangle has side lengths \(a\) units and \(b\) units, the area is \(a \boldcdot b\) square units. For example, if we have a rectangle with \(\frac12\)-inch side lengths, its area is \(\frac12 \boldcdot \frac12\) or \(\frac14\) square inches.

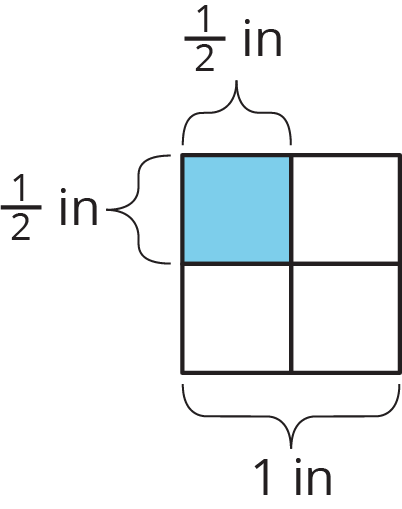
A square. 

This means that if we know the area and one side length of a rectangle, we can divide to find the other side length.

A rectangle with the horizontal side labeled 10 and one half inches and the vertical side labeled with a question mark. In the center of the rectangle, 89 and one fourth square inches is indicated.


 

If one side length of a rectangle is \(10\frac12\) in and its area is \(89\frac14\) in2, we can write this equation to show their relationship: \(\displaystyle 10\frac12  \boldcdot {?} =89\frac14\)

Then, we can find the other side length, in inches, using division: \(\displaystyle 89\frac14 \div 10\frac12 = {?}\)