Lesson 2
Adjacent Angles
Lesson Narrative
In this lesson, students are introduced to the terms complementary, for describing two angles whose measures add to \(90^\circ\), and supplementary, for describing two angles whose measures add to \(180^\circ\). They practice finding an unknown angle given the measure of another angle that is complementary or supplementary.
Many of the angles in this lesson share the same vertex as another angle, so students need to be careful when naming each angle (MP6) in addition to describing the relationship between pairs of angles.
Learning Goals
Teacher Facing
- Comprehend the terms “complementary” and “supplementary” (in spoken and written language) as they describe pairs of angles.
- Explain (orally and in writing) how to find an unknown angle measure, given adjacent complementary or supplementary angles.
- Generalize (orally) that when a straight angle or a right angle is decomposed, the measures of the resulting angles add up to $180^\circ$ or $90^\circ$, respectively.
Student Facing
Let’s look at some special pairs of angles.
Required Preparation
Cut blank paper in half so that each student can have 2 half sheets of paper. It is very important that these cuts are completely straight and exactly perpendicular to the sides being cut for this activity to work.
Prepare to distribute scissors, straightedges, and protractors.
Learning Targets
Student Facing
- I can find unknown angle measures by reasoning about complementary or supplementary angles.
- I can recognize when adjacent angles are complementary or supplementary.
Glossary Entries
-
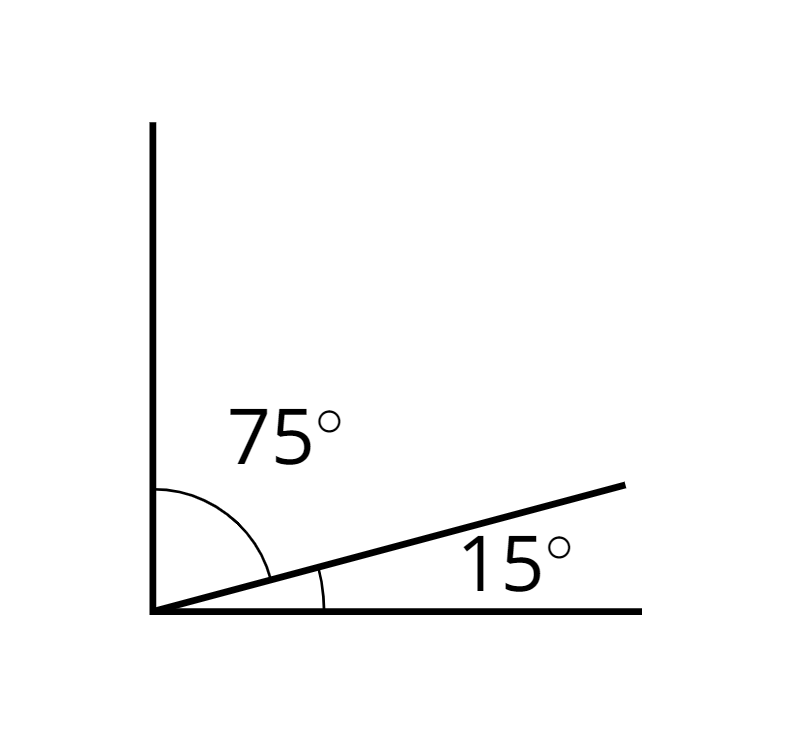
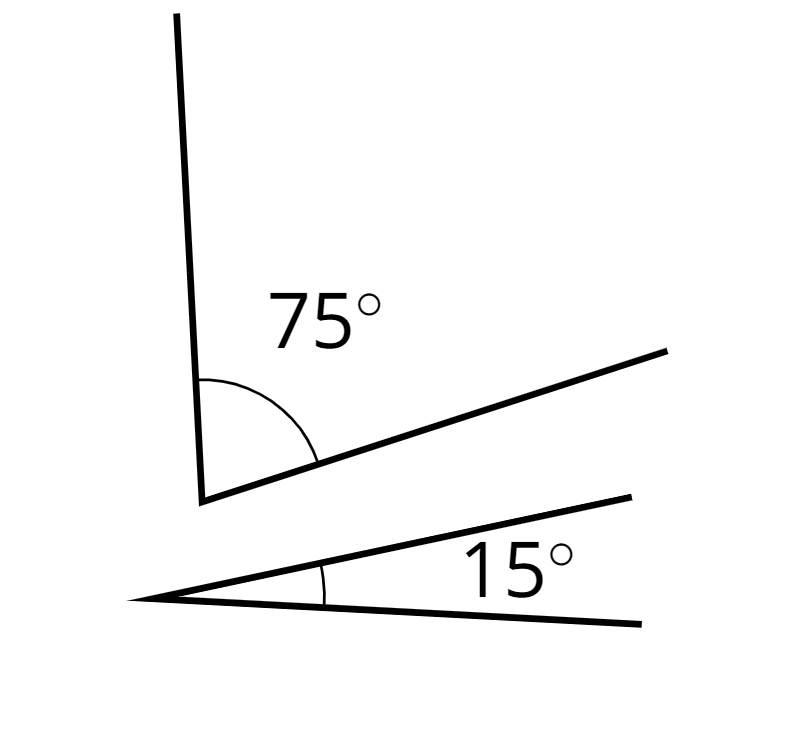
complementary
Complementary angles have measures that add up to 90 degrees.
For example, a \(15^\circ\) angle and a \(75^\circ\) angle are complementary.
-
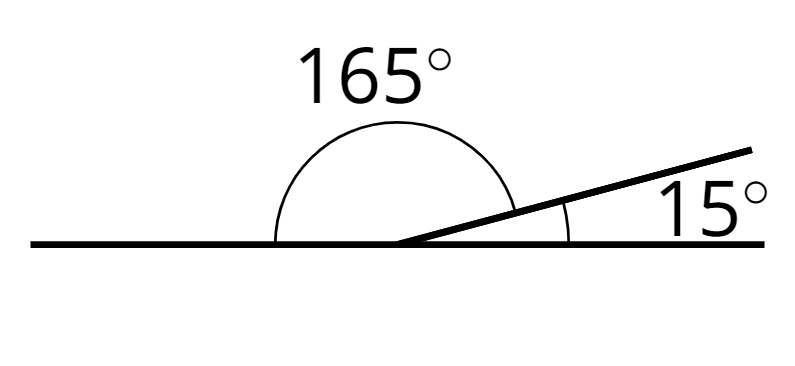
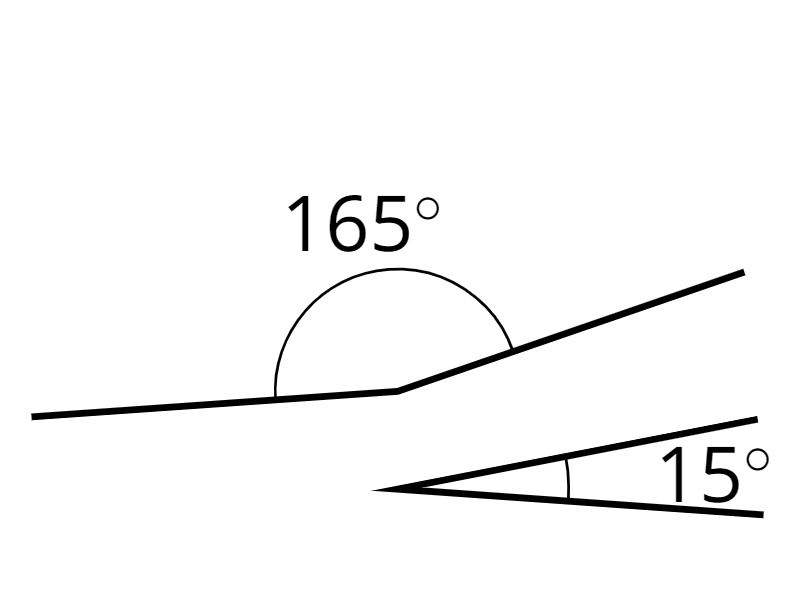
supplementary
Supplementary angles have measures that add up to 180 degrees.
For example, a \(15^\circ\) angle and a \(165^\circ\) angle are supplementary.
Print Formatted Materials
For access, consult one of our IM Certified Partners.
Additional Resources
| Google Slides | For access, consult one of our IM Certified Partners. |
|
| PowerPoint Slides | For access, consult one of our IM Certified Partners. |