Lesson 12
Volume of Right Prisms
Let’s look at volumes of prisms.
12.1: Three Prisms with the Same Volume
Rectangles A, B, and C represent bases of three prisms.
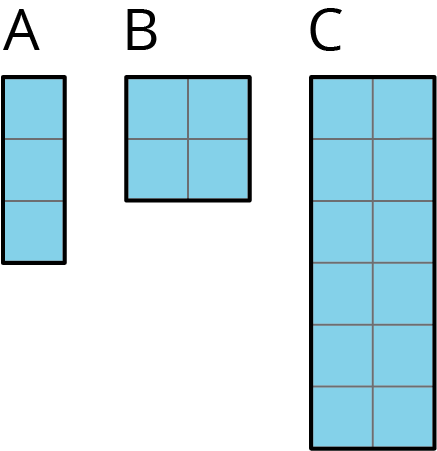
- If each prism has the same height, which one will have the greatest volume, and which will have the least? Explain your reasoning.
-
If each prism has the same volume, which one will have the tallest height, and which will have the shortest? Explain your reasoning.
12.2: Finding Volume with Cubes
This applet has 64 snap cubes, all sitting in the same spot on the screen, like a hidden stack of blocks. You will always know where the stack is because it sits on a gray square. You can keep dragging blocks out of the pile by their red points until you have enough to build what you want.

Click on the red points to change from left/right movement to up/down movement.
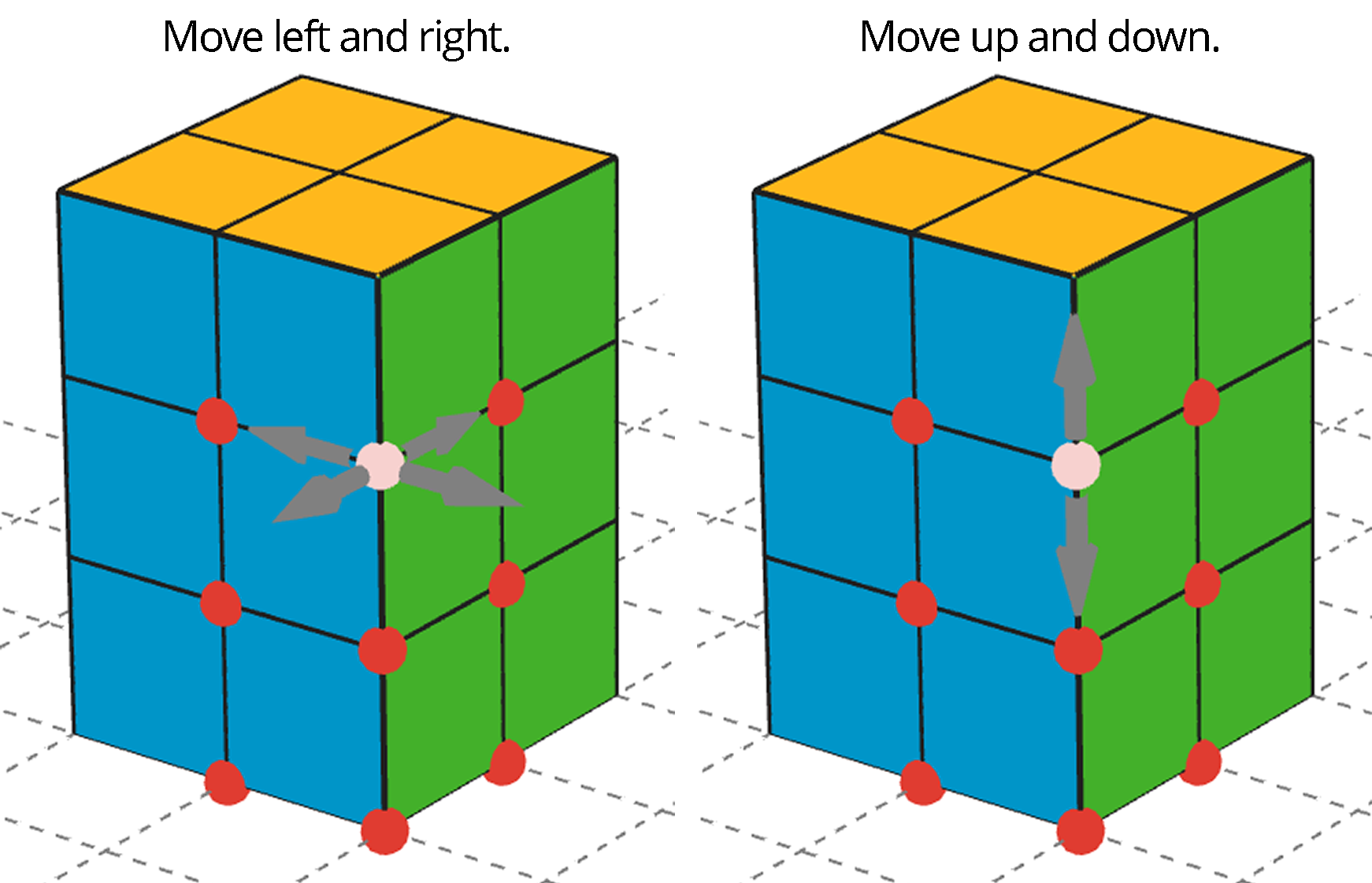
There is also a shape on the grid. It marks the footprint of the shapes you will be building.
- Using the face of a snap cube as your area unit, what is the area of the shape? Explain or show your reasoning.
- Use snap cubes to build the shape from the paper. Add another layer of cubes on top of the shape you have built. Describe this three-dimensional object.
- What is the volume of your object? Explain your reasoning.
- Right now, your object has a height of 2. What would the volume be
-
if it had a height of 5?
-
if it had a height of 8.5?
-
12.3: Can You Find the Volume?
The applet has a set of three-dimensional figures.
- For each figure, determine whether the shape is a prism.
- For each prism:
- Find the area of the base of the prism.
- Find the height of the prism.
- Calculate the volume of the prism.
| Is it a prism? | area of prism base (cm2) | height (cm) | volume (cm3) |
|---|---|---|---|
- Begin by grabbing the gray bar on the left and dragging it to the right until you see the slider.
- Choose a figure using the slider.
- Rotate the view using the Rotate 3D Graphics tool marked by two intersecting, curved arrows.
- Note that each polyhedron has only one label per unique face. Where no measurements are shown, the faces are identical copies.
- Use the distance tool, marked with the "cm," to click on any segment and find the height or length.
- Troubleshooting tip: the cursor must be on the 3D Graphics window for the full toolbar to appear.
Imagine a large, solid cube made out of 64 white snap cubes. Someone spray paints all 6 faces of the large cube blue. After the paint dries, they disassemble the large cube into a pile of 64 snap cubes.
- How many of those 64 snap cubes have exactly 2 faces that are blue?
- What are the other possible numbers of blue faces the cubes can have? How many of each are there?
- Try this problem again with some larger-sized cubes that use more than 64 snap cubes to build. What patterns do you notice?
12.4: What’s the Prism’s Height?
There are 4 different prisms that all have the same volume. Here is what the base of each prism looks like.
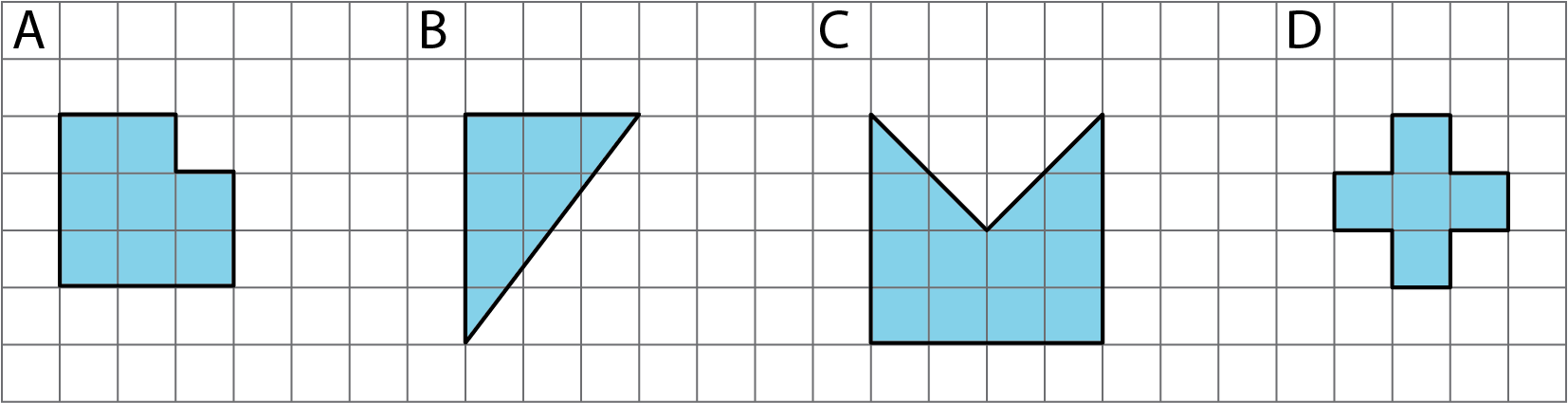
-
Order the prisms from shortest to tallest. Explain your reasoning.
-
If the volume of each prism is 60 units3, what would be the height of each prism?
- For a volume other than 60 units3, what could be the height of each prism?
-
Discuss your thinking with your partner. If you disagree, work to reach an agreement.
Summary
Any cross section of a prism that is parallel to the base will be identical to the base. This means we can slice prisms up to help find their volume. For example, if we have a rectangular prism that is 3 units tall and has a base that is 4 units by 5 units, we can think of this as 3 layers, where each layer has \(4\boldcdot 5\) cubic units.

That means the volume of the original rectangular prism is \(3(4\boldcdot 5)\) cubic units.
This works with any prism! If we have a prism with height 3 cm that has a base of area 20 cm2, then the volume is \(3\boldcdot 20\) cm3 regardless of the shape of the base. In general, the volume of a prism with height \(h\) and area \(B\) is
\(\displaystyle V = B \boldcdot h\)
For example, these two prisms both have a volume of 100 cm3.

Glossary Entries
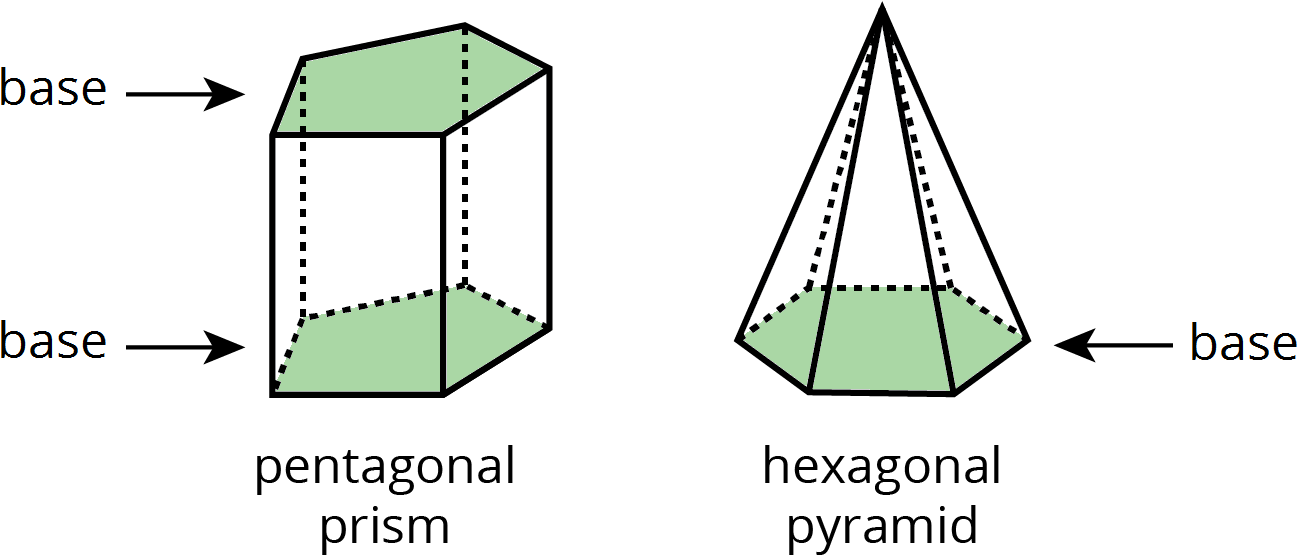
- base (of a prism or pyramid)
The word base can also refer to a face of a polyhedron.
A prism has two identical bases that are parallel. A pyramid has one base.
A prism or pyramid is named for the shape of its base.
- cross section
A cross section is the new face you see when you slice through a three-dimensional figure.
For example, if you slice a rectangular pyramid parallel to the base, you get a smaller rectangle as the cross section.
- prism
A prism is a type of polyhedron that has two bases that are identical copies of each other. The bases are connected by rectangles or parallelograms.
Here are some drawings of prisms.

- pyramid
A pyramid is a type of polyhedron that has one base. All the other faces are triangles, and they all meet at a single vertex.
Here are some drawings of pyramids.
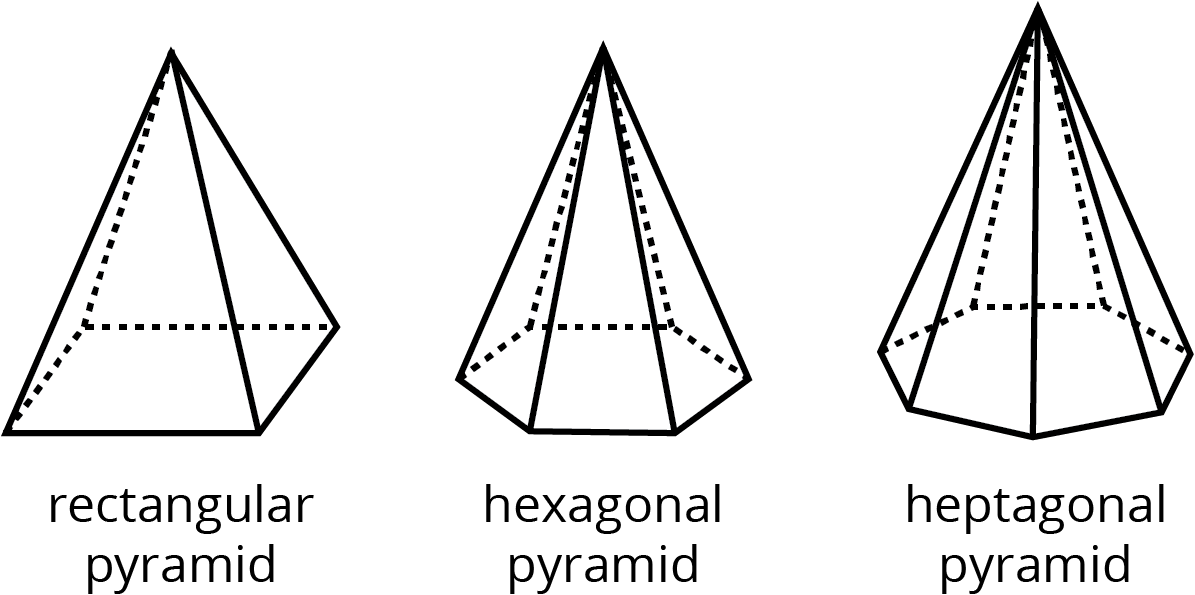
- volume
Volume is the number of cubic units that fill a three-dimensional region, without any gaps or overlaps.
For example, the volume of this rectangular prism is 60 units3, because it is composed of 3 layers that are each 20 units3.
