Lesson 1
Relationships of Angles
Problem 1
Here are questions about two types of angles.
- Draw a right angle. How do you know it's a right angle? What is its measure in degrees?
- Draw a straight angle. How do you know it’s a straight angle? What is its measure in degrees?
Solution
For access, consult one of our IM Certified Partners.
Problem 2
An equilateral triangle’s angles each have a measure of 60 degrees.
-
Can you put copies of an equilateral triangle together to form a straight angle? Explain or show your reasoning.
-
Can you put copies of an equilateral triangle together to form a right angle? Explain or show your reasoning.
Solution
For access, consult one of our IM Certified Partners.
Problem 3
Here is a square and some regular octagons.
In this pattern, all of the angles inside the octagons have the same measure. The shape in the center is a square. Find the measure of one of the angles inside one of the octagons.
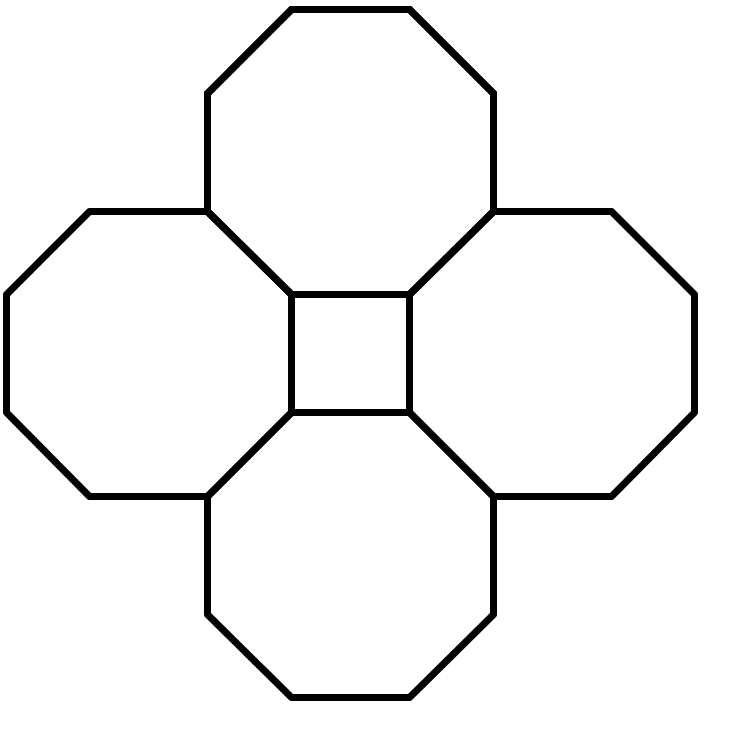
Solution
For access, consult one of our IM Certified Partners.
Problem 4
The height of the water in a tank decreases by 3.5 cm each day. When the tank is full, the water is 10 m deep. The water tank needs to be refilled when the water height drops below 4 m.
- Write a question that could be answered by solving the equation \(10-0.035d=4\).
- Is 100 a solution of \(10-0.035d>4\)? Write a question that solving this problem could answer.
Solution
For access, consult one of our IM Certified Partners.
(From Unit 6, Lesson 17.)Problem 5
Use the distributive property to write an expression that is equivalent to each given expression.
- \(\text-3(2x-4)\)
- \(0.1(\text-90+50a)\)
- \(\text-7(\text-x-9)\)
- \(\frac45(10y+\text-x+\text-15)\)
Solution
For access, consult one of our IM Certified Partners.
(From Unit 6, Lesson 18.)Problem 6
Lin’s puppy is gaining weight at a rate of 0.125 pounds per day. Describe the weight gain in days per pound.
Solution
For access, consult one of our IM Certified Partners.
(From Unit 2, Lesson 3.)