Lesson 15
Quartiles and Interquartile Range
Let's look at other measures for describing distributions.
Problem 1
Suppose that there are 20 numbers in a data set and that they are all different.
- How many of the values in this data set are between the first quartile and the third quartile?
- How many of the values in this data set are between the first quartile and the median?
Problem 2
In a word game, 1 letter is worth 1 point. This dot plot shows the scores for 20 common words.
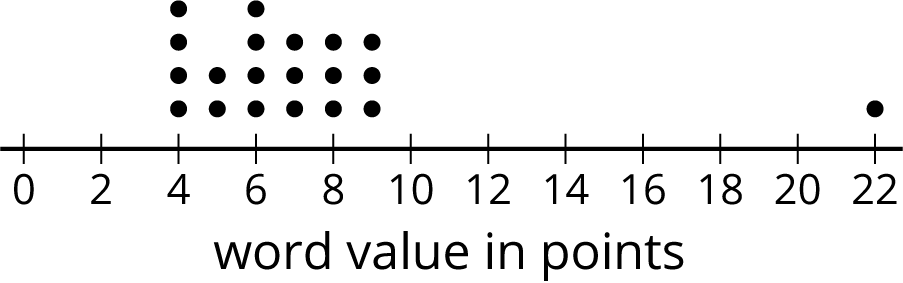
- What is the median score?
- What is the first quartile (Q1)?
- What is the third quartile (Q3)?
- What is the interquartile range (IQR)?
Problem 3
Mai and Priya each played 10 games of bowling and recorded the scores. Mai’s median score was 120, and her IQR was 5. Priya’s median score was 118, and her IQR was 15. Whose scores probably had less variability? Explain how you know.
Problem 4
Here are five dot plots that show the amounts of time that ten sixth-grade students in five countries took to get to school. Match each dot plot with the appropriate median and IQR.
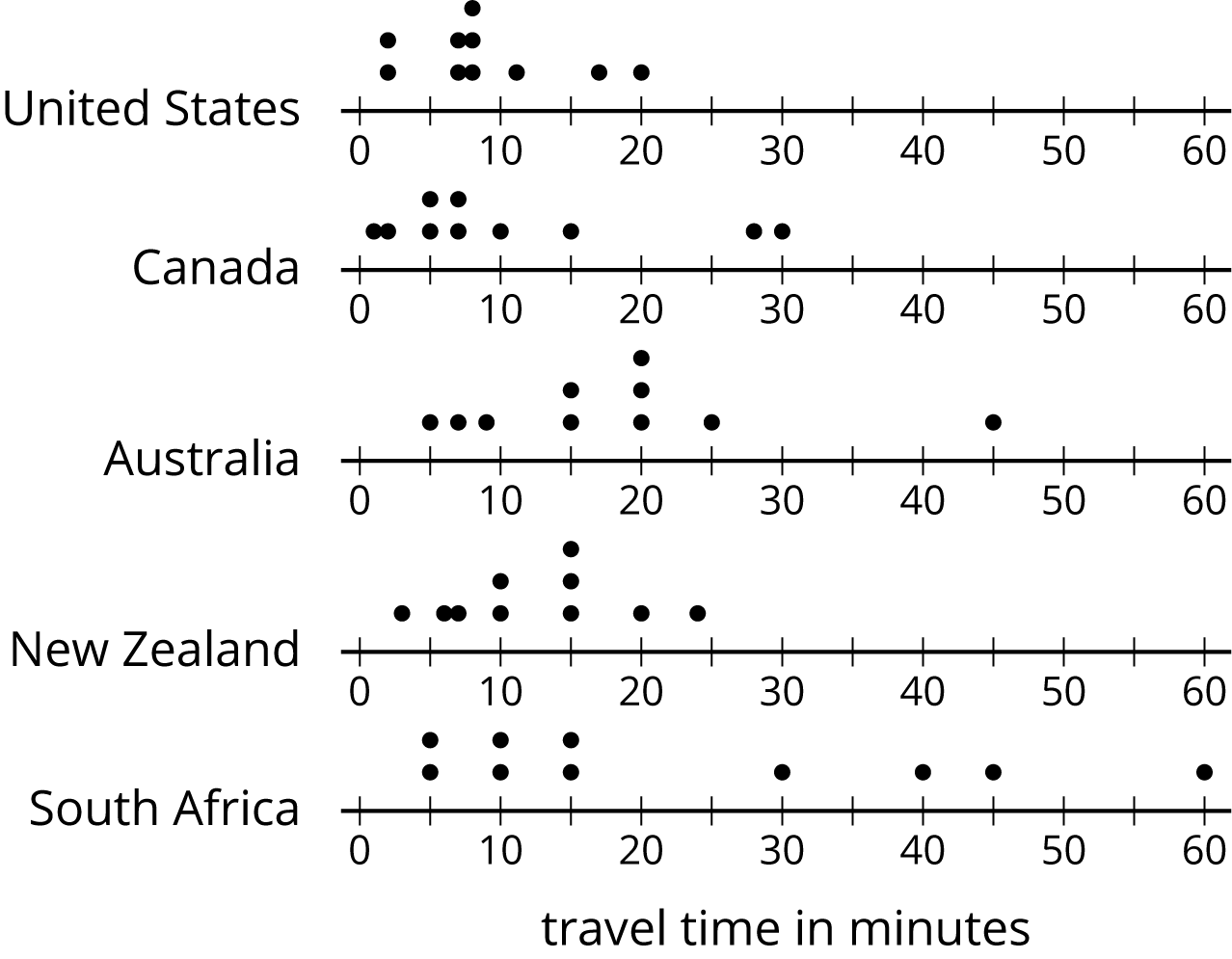
- Median: 17.5, IQR: 11
- Median: 15, IQR: 30
- Median: 8, IQR: 4
- Median: 7, IQR: 10
- Median: 12.5, IQR: 8
Problem 5
Draw and label an appropriate pair of axes and plot the points. \(A = (10, 50)\), \(B = (30, 25)\), \(C = (0, 30)\), \(D = (20, 35)\)
Problem 6
There are 20 pennies in a jar. If 16% of the coins in the jar are pennies, how many coins are there in the jar?