Lesson 6

Here is a dot plot showing the weights, in pounds, of 40 dogs at a dog show.

1. Write two statistical questions that can be answered using the dot plot.
2. What would you consider a typical weight for a dog at this dog show? Explain your reasoning.

Here is a histogram that shows some dog weights in pounds.

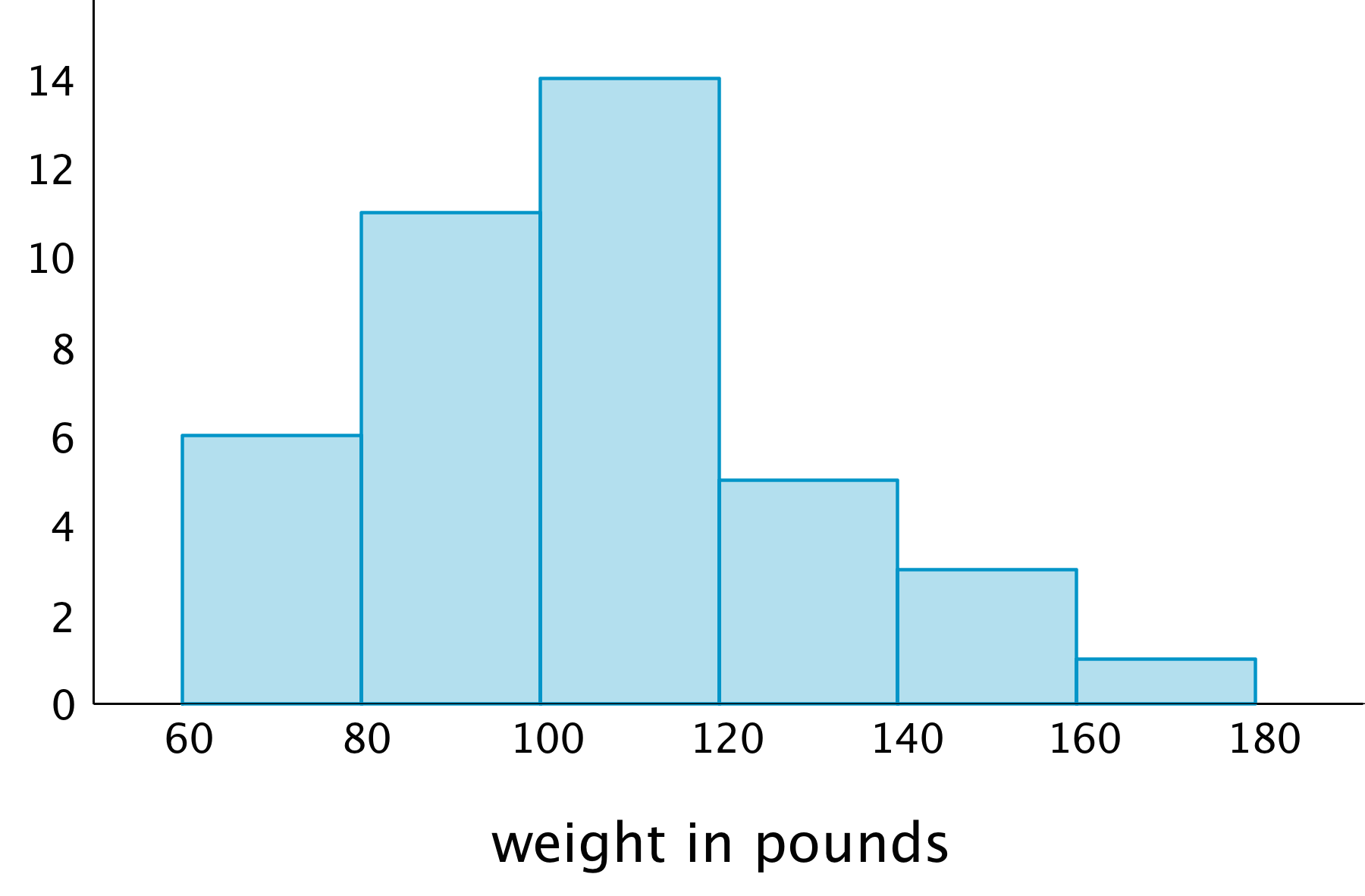
Each bar includes the left-end value but not the right-end value. For example, the first bar includes dogs that weigh 60 pounds and 68 pounds but not 80 pounds.

1. Use the histogram to answer the following questions.

   1. How many dogs weigh at least 100 pounds?

   2. How many dogs weigh exactly 70 pounds?

   3. How many dogs weigh at least 120 and less than 160 pounds?

   4. How much does the heaviest dog at the show weigh?

   5. What would you consider a typical weight for a dog at this dog show? Explain your reasoning.

2. Discuss with a partner:

   • If you used the dot plot to answer the same five questions you just answered, how would your answers be different?

   • How are the histogram and the dot plot alike? How are they different?

Every ten years, the United States conducts a census, which is an effort to count the entire population. The dot plot shows the population data from the 2010 census for each of the fifty states and the District of Columbia (DC).

1. Here are some statistical questions about the population of the fifty states and DC. How difficult would it be to answer the questions using the dot plot?

   In the middle column, rate each question with an E (easy to answer), H (hard to answer), or I (impossible to answer). Be prepared to explain your reasoning.

   statistical question	using the dot plot	using the histogram
   a. How many states have populations greater than 15 million?
   b. Which states have populations greater than 15 million?
   c. How many states have populations less than 5 million?
   d. What is a typical state population?
   e. Are there more states with fewer than 5 million people or more states with between 5 and 10 million people?
   f. How would you describe the distribution of state populations?

2. Here are the population data for all states and the District of Columbia from the 2010 census. Use the information to complete the table.

   

   

   population (millions)	frequency
   0–5
   5–10
   10–15
   15–20
   20–25
   25–30
   30–35
   35–40

3. Use the grid and the information in your table to create a histogram.

   

   

4. Return to the statistical questions at the beginning of the activity. Which ones are now easier to answer?

   In the last column of the table, rate each question with an E (easy), H (hard), and I (impossible) based on how difficult it is to answer them. Be prepared to explain your reasoning.

In addition to using dot plots, we can also represent distributions of numerical data using histograms.

Here is a dot plot that shows the weights, in kilograms, of 30 dogs, followed by a histogram that shows the same distribution.

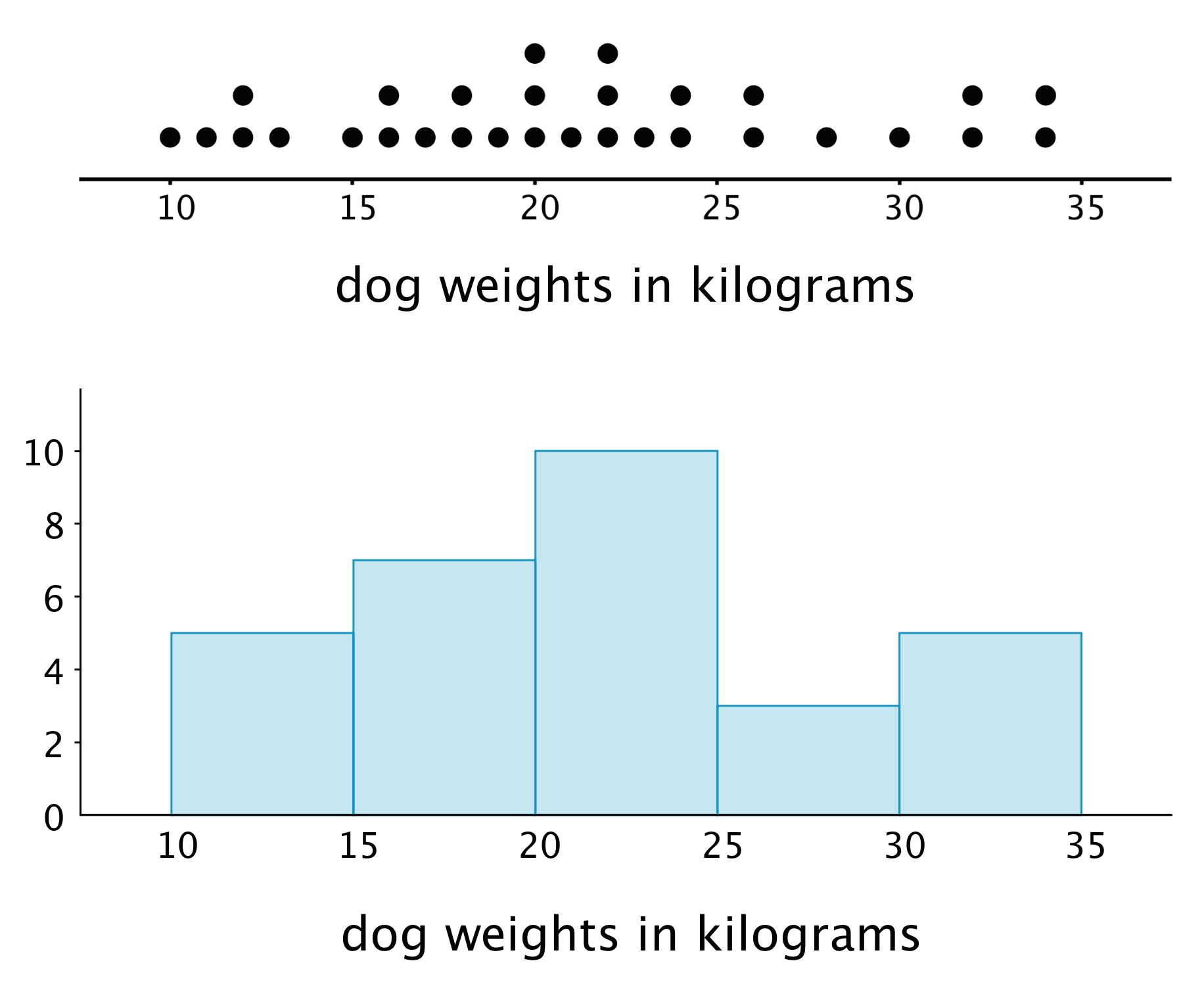
In a histogram, data values are placed in groups or “bins” of a certain size, and each group is represented with a bar. The height of the bar tells us the frequency for that group.

For example, the height of the tallest bar is 10, and the bar represents weights from 20 to less than 25 kilograms, so there are 10 dogs whose weights fall in that group. Similarly, there are 3 dogs that weigh anywhere from 25 to less than 30 kilograms.

Notice that the histogram and the dot plot have a similar shape. The dot plot has the advantage of showing all of the data values, but the histogram is easier to draw and to interpret when there are a lot of values or when the values are all different.

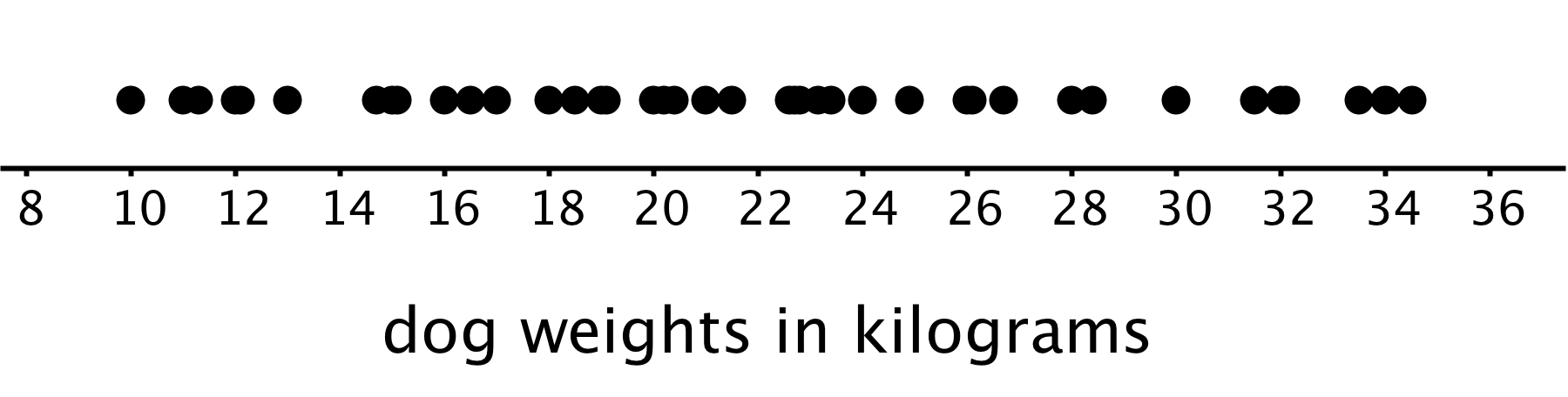
Here is a dot plot showing the weight distribution of 40 dogs. The weights were measured to the nearest 0.1 kilogram instead of the nearest kilogram.

Here is a histogram showing the same distribution.

In this case, it is difficult to make sense of the distribution from the dot plot because the dots are so close together and all in one line. The histogram of the same data set does a much better job showing the distribution of weights, even though we can’t see the individual data values.