Lesson 16

Here are the birth weights, in ounces, of all the puppies born at a kennel in the past month.

• 13
• 14
• 15
• 15
• 16
• 16
• 16
• 16
• 17
• 17
• 17
• 17
• 17
• 17
• 17
• 18
• 18
• 18
• 18
• 18
• 18
• 18
• 18
• 19
• 20

What do you notice and wonder about the distribution of the puppy weights?

Your teacher will give you the data on the lengths of names of students in your class. Write the five-number summary by finding the data set's minimum, Q1, Q2, Q3, and the maximum.

Pause for additional instructions from your teacher.

Twenty people participated in a study about blinking. The number of times each person blinked while watching a video for one minute was recorded. The data values are shown here, in order from smallest to largest.

• 3
• 6
• 8
• 11
• 11
• 13
• 14
• 14
• 14
• 14
• 16
• 18
• 20
• 20
• 20
• 22
• 24
• 32
• 36
• 51

1. 1. Use the grid and axis to make a dot plot of this data set.

      

      

   2. Find the median (Q2) and mark its location on the dot plot.
   3. Find the first quartile (Q1) and the third quartile (Q3). Mark their locations on the dot plot.

   4. What are the minimum and maximum values?

2. A box plot can be used to represent the five-number summary graphically. Let’s draw a box plot for the number-of-blinks data. On the grid, above the dot plot:

   1. Draw a box that extends from the first quartile (Q1) to the third quartile (Q3). Label the quartiles.
   2. At the median (Q2), draw a vertical line from the top of the box to the bottom of the box. Label the median.
   3. From the left side of the box (Q1), draw a horizontal line (a whisker) that extends to the minimum of the data set. On the right side of the box (Q3), draw a similar line that extends to the maximum of the data set.

3. You have now created a box plot to represent the number of blinks data. What fraction of the data values are represented by each of these elements of the box plot?

   1. The left whisker
   2. The box
   3. The right whisker

A box plot represents the five-number summary of a data set.

It shows the first quartile (Q1) and the third quartile (Q3) as the left and right sides of a rectangle or a box. The median (Q2) is shown as a vertical segment inside the box. On the left side, a horizontal line segment—a “whisker”—extends from Q1 to the minimum value. On the right, a whisker extends from Q3 to the maximum value.

The rectangle in the middle represents the middle half of the data. Its width is the IQR. The whiskers represent the bottom quarter and top quarter of the data set.

Earlier we saw dot plots representing the weights of pugs and beagles. The box plots for these data sets are shown above the corresponding dot plots. 

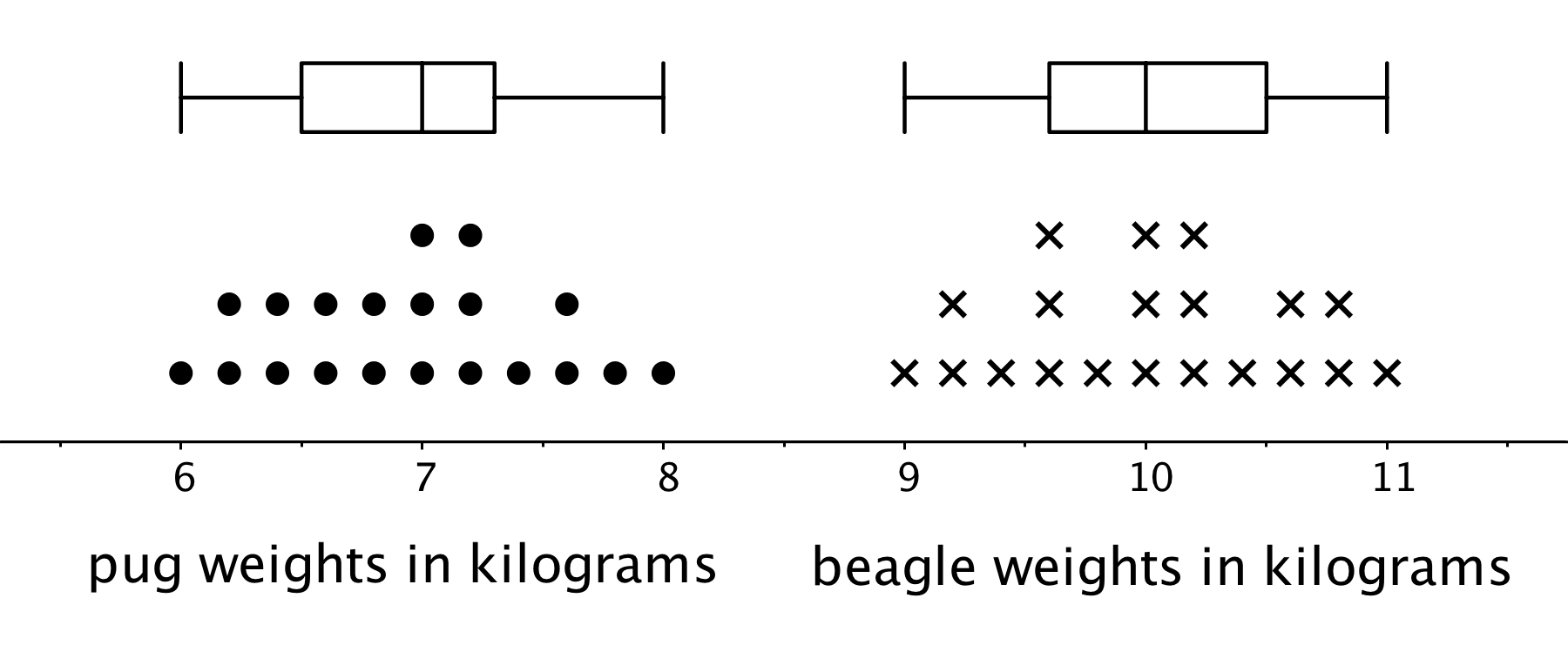
We can tell from the box plots that, in general, the pugs in the group are lighter than the beagles: the median weight of pugs is 7 kilograms and the median weight of beagles is 10 kilograms. Because the two box plots are on the same scale and the rectangles have similar widths, we can also tell that the IQRs for the two breeds are very similar. This suggests that the variability in the beagle weights is very similar to the variability in the pug weights.