Lesson 12
Using Mean and MAD to Make Comparisons
Let's use mean and MAD to describe and compare distributions.
Problem 1
The dot plots show the amounts of time that ten U.S. students and ten Australian students took to get to school.

Which statement is true about the MAD of the Australian data set?
It is significantly less than the MAD of the U.S. data set.
It is exactly equal to the MAD of the U.S. data set.
It is approximately equal to the MAD of the U.S. data set.
It is significantly greater than the MAD of the U.S. data set.
Problem 2
The dot plots show the amounts of time that ten South African students and ten Australian students took to get to school. Without calculating, answer the questions.
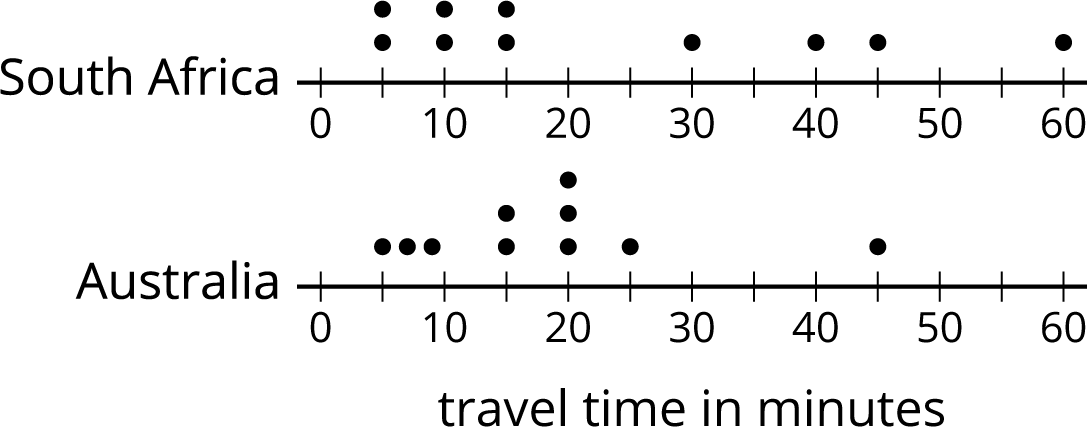
-
Which data set has the smaller mean? Explain your reasoning.
-
Which data set has the smaller MAD? Explain your reasoning.
-
What does a smaller mean tell us in this context?
- What does a smaller MAD tell us in this context?
Problem 3
Two high school basketball teams have identical records of 15 wins and 2 losses. Sunnyside High School's mean score is 50 points and its MAD is 4 points. Shadyside High School's mean score is 60 points and its MAD is 15 points.
Lin read the records of each team’s score. She likes the team that had nearly the same score for every game it played. Which team do you think Lin likes? Explain your reasoning.
Problem 4
Jada thinks the perimeter of this rectangle can be represented with the expression \(a+a+b+b\). Andre thinks it can be represented with \(2a+2b\). Do you agree with either of them? Explain your reasoning.
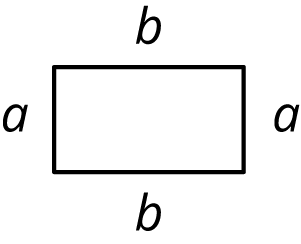
Problem 5
Draw a number line.
- Plot and label three numbers between -2 and -8 (not including -2 and -8).
-
Use the numbers you plotted and the symbols \(<\) and \(>\) to write three inequality statements.
Problem 6
Adult elephant seals generally weigh about 5,500 pounds. If you weighed 5 elephant seals, would you expect each seal to weigh exactly 5,500 pounds? Explain your reasoning.