Lesson 18

What a Point in a Scatter Plot Means

Let’s investigate points in scatter plots.

Problem 1

Here is a table and a scatter plot that compares points per game to free throw attempts for a basketball team during a tournament.

player

free throw
attempts

 points
player A 5.5 28.3
player B 2.1 18.6
player C 4.1 13.7
player D 1.6 10.6
player E 3.1 10.4
player F 1 5
player G 1.2 5
player H 0.7 4.7
player I 1.5 3.7
player J 1.5 3.5
player K 1.2 3.1
player L 0 1
player M 0 0.8
player N 0 0.6
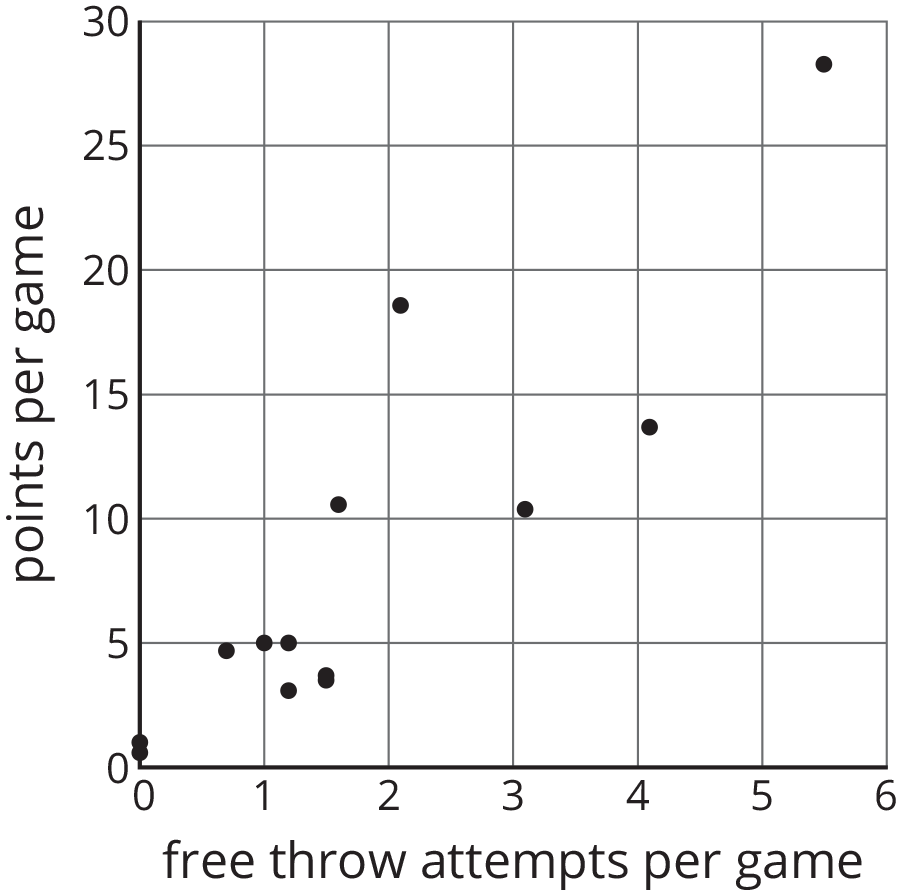
Scatterplot, free throw attempts per game, 0 to 6 by 1, points per game, 0 to 30 by 5. Points given by accompanying table.

  1. Circle the point that represents the data for Player E.
  2. What does the point \((2.1,18.6)\) represent?
     
  3. In that same tournament, Player O on another team scored 14.3 points per game with 4.8 free throw attempts per game. Plot a point on the graph that shows this information.

Problem 2

Andre said, “I found two figures that are congruent, so they can’t be similar.”

Diego said, “No, they are similar! The scale factor is 1.”

Do you agree with either of them? Use the definition of similarity to explain your answer.

(From Unit 2, Lesson 11.)

Problem 3

For each equation, explain what you could do first to each side of the equation so that there would be no fractions. You do not have to solve the equations (unless you want more practice).

  1. \(\dfrac{3x-4}{8} = \dfrac{x+2}{3}\)
  2. \(\dfrac{3(2-r)}{4} = \dfrac{3+r}{6}\)
  1. \(\dfrac{4p+3}{8} = \dfrac{p+2}{4}\)
  2. \(\dfrac{2(a-7)}{15} = \dfrac{a+4}{6}\)
(From Unit 4, Lesson 14.)

Problem 4

The points \((\text-2,0)\) and \((0,\text-6)\) are each on the graph of a linear equation. Is \((2,6)\) also on the graph of this linear equation? Explain your reasoning.

(From Unit 5, Lesson 11.)