Lesson 6
The Median
Problem 1
Here is data that shows a student's scores for 10 rounds of a video game.
130
150
120
170
130
120
160
160
190
140
What is the median score?
125
145
147
150
Problem 2
When he sorts the class’s scores on the last test, the teacher notices that exactly 12 students scored better than Clare and exactly 12 students scored worse than Clare. Does this mean that Clare’s score on the test is the median? Explain your reasoning.
Problem 3
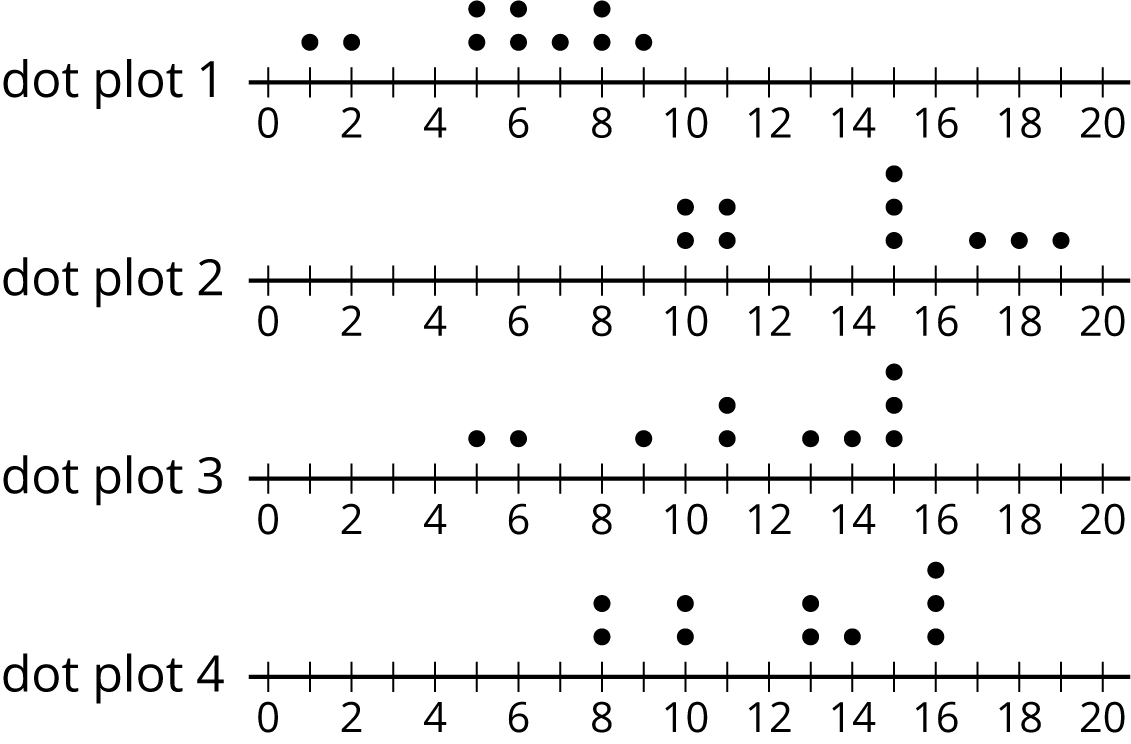
The medians of the following dot plots are 6, 12, 13, and 15, but not in that order. Match each dot plot with its median.
Problem 4
Ten sixth-grade students reported the hours of sleep they get on nights before a school day. Their responses are recorded in the dot plot.
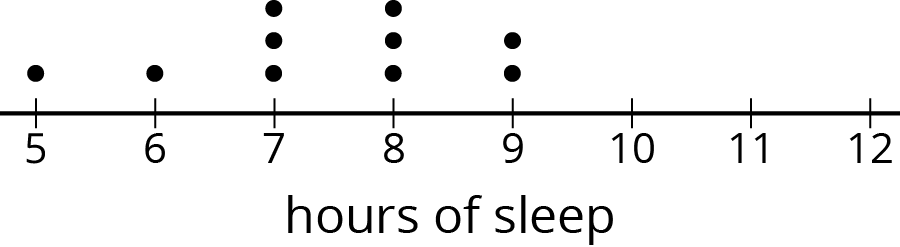
Looking at the dot plot, Lin estimated the mean number of hours of sleep to be 8.5 hours. Noah's estimate was 7.5 hours. Diego's estimate was 6.5 hours.
Which estimate do you think is best? Explain how you know.
Problem 5
In his history class, Han's homework scores are:
100
100
100
100
95
100
90
100
0
The history teacher uses the mean to calculate the grade for homework. Write an argument for Han to explain why median would be a better measure to use for his homework grades.
Problem 6
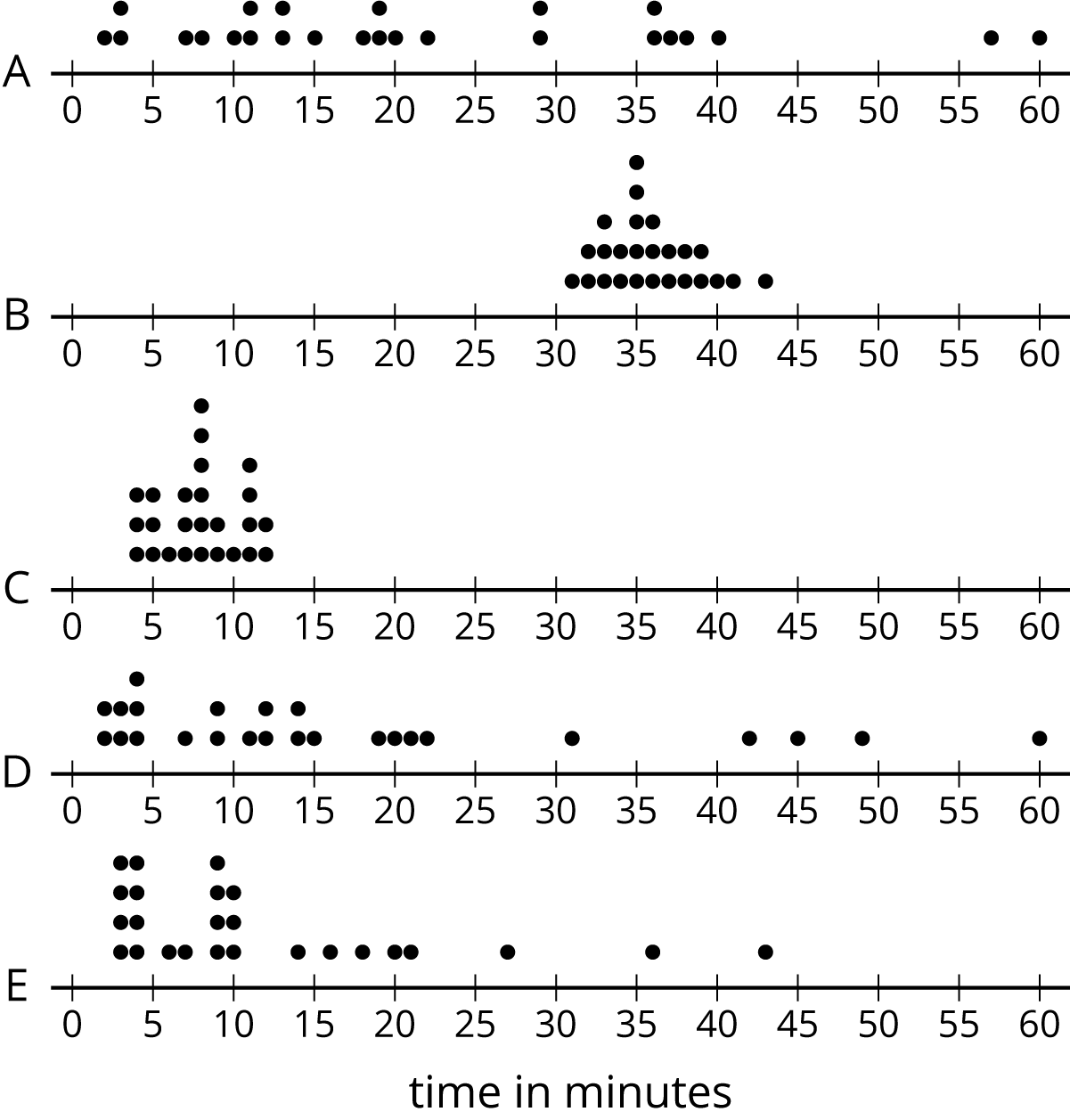
The dot plots show how much time, in minutes, students in a class took to complete each of five different tasks. Select all the dot plots of tasks for which the mean time is approximately equal to the median time.
Problem 7
Here is a set of coordinates. Draw and label an appropriate pair of axes and plot the points. \(A = (1, 0)\), \(B = (0, 0.5)\), \(C= (4, 3.5)\), \(D = (1.5, 0.5)\)