Lesson 9
What Makes a Good Sample?
Let’s see what makes a good sample.
9.1: Number Talk: Division by Powers of 10
Find the value of each quotient mentally.
\(34,\!000\div10\)
\(340\div100\)
\(34\div10\)
\(3.4\div100\)
9.2: Selling Paintings
Your teacher will assign you to work with either means or medians.
-
A young artist has sold 10 paintings. Calculate the measure of center you were assigned for each of these samples:
-
The first two paintings she sold were for $50 and $350.
-
At a gallery show, she sold three paintings for $250, $400, and $1,200.
-
Her oil paintings have sold for $410, $400, and $375.
-
-
Here are the selling prices for all 10 of her paintings:
$50
$200
$250
$275
$280
$350
$375
$400
$410
$1,200
Calculate the measure of center you were assigned for all of the selling prices.
- Compare your answers with your partner. Were the measures of center for any of the samples close to the same measure of center for the population?
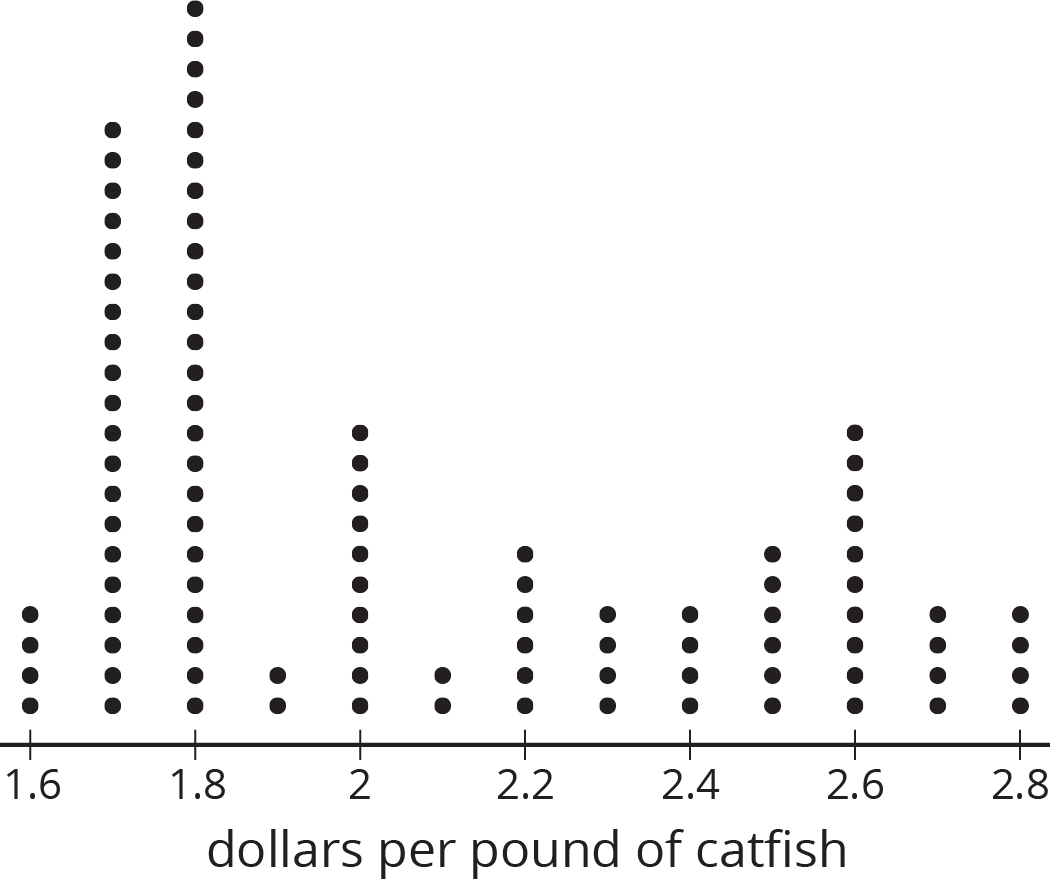
9.3: Sampling the Fish Market
The price per pound of catfish at a fish market was recorded for 100 weeks.
- Here are dot plots showing the population and three different samples from that population. What do you notice? What do you wonder?
- If the goal is to have the sample represent the population, which of the samples would work best? Which wouldn't work so well? Explain your reasoning.
To use this applet, drag the gray bar at the bottom up to see the sample dot plots.
When doing a statistical study, it is important to keep the goal of the study in mind. Representative samples give us the best information about the distribution of the population as a whole, but sometimes a representative sample won’t work for the goal of a study!
For example, suppose you want to study how discrimination affects people in your town. Surveying a representative sample of people in your town would give information about how the population generally feels, but might miss some smaller groups. Describe a way you might choose a sample of people to address this question.
9.4: Auditing Sales
An online shopping company tracks how many items they sell in different categories during each month for a year. Three different auditors each take samples from that data. Use the samples to draw dot plots of what the population data might look like for the furniture and electronics categories.
Auditor 1’s sample

Auditor 2’s sample
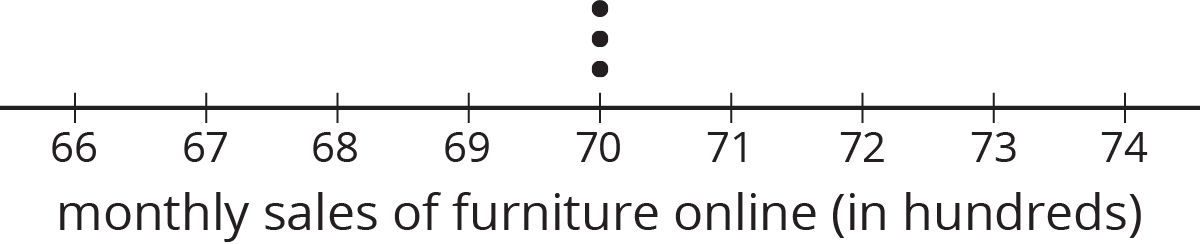
Auditor 3’s sample

Population

Auditor 1’s sample

Auditor 2’s sample

Auditor 3’s sample

Population
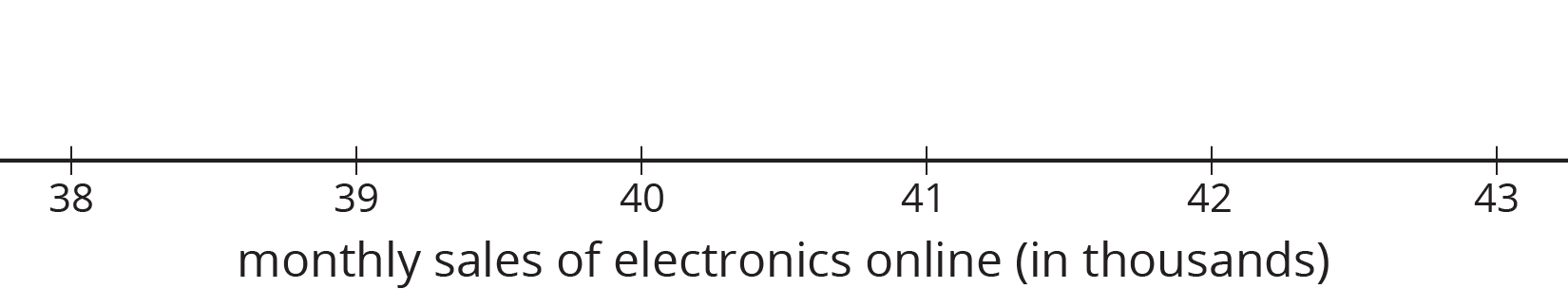
Summary
A sample that is representative of a population has a distribution that closely resembles the distribution of the population in shape, center, and spread.
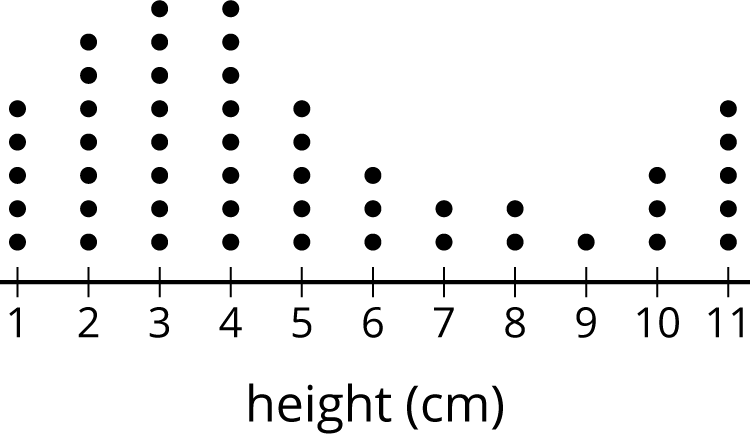
For example, consider the distribution of plant heights, in cm, for a population of plants shown in this dot plot. The mean for this population is 4.9 cm, and the MAD is 2.6 cm.
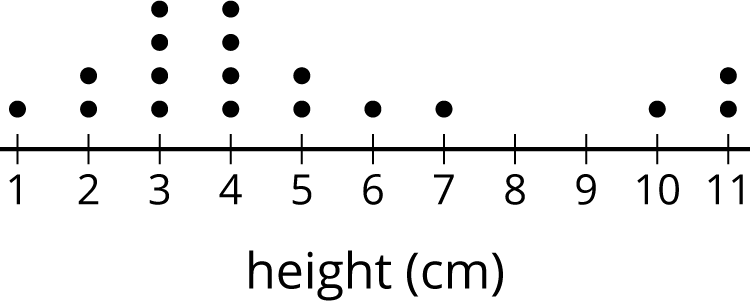
A representative sample of this population should have a larger peak on the left and a smaller one on the right, like this one. The mean for this sample is 4.9 cm, and the MAD is 2.3 cm.
Here is the distribution for another sample from the same population. This sample has a mean of 5.7 cm and a MAD of 1.5 cm. These are both very different from the population, and the distribution has a very different shape, so it is not a representative sample.
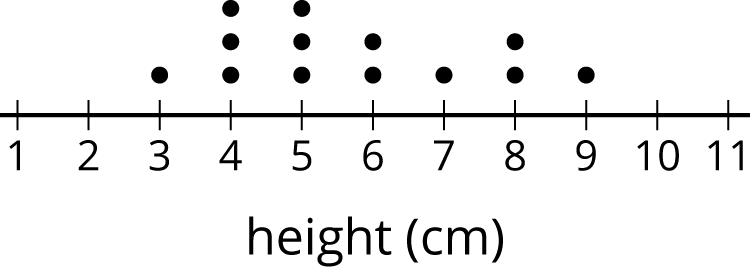
Glossary Entries
- population
A population is a set of people or things that we want to study.
For example, if we want to study the heights of people on different sports teams, the population would be all the people on the teams.
- representative
A sample is representative of a population if its distribution resembles the population's distribution in center, shape, and spread.
For example, this dot plot represents a population.
This dot plot shows a sample that is representative of the population.
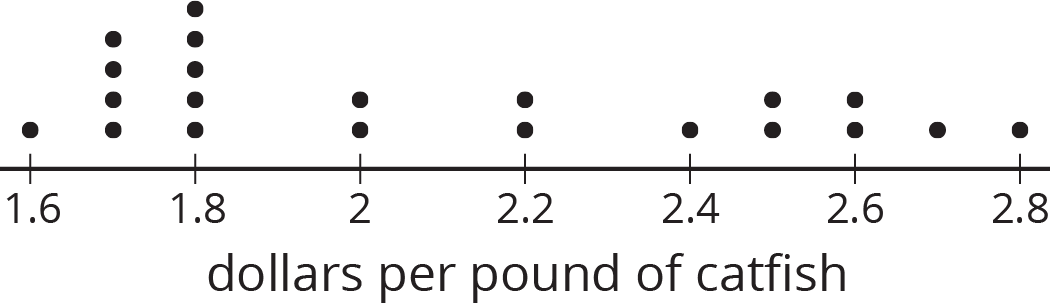
- sample
A sample is part of a population. For example, a population could be all the seventh grade students at one school. One sample of that population is all the seventh grade students who are in band.