Lesson 7

Here are dot plots that show the ages of people at two different parties. The mean of each distribution is marked with a triangle.

What do you notice and what do you wonder about the distributions in the two dot plots?

Here are the ages of the people at one party, listed from least to greatest.

• 7
• 8
• 9
• 10
• 10
• 11
• 12
• 15
• 16
• 20
• 20
• 22
• 23
• 24
• 28
• 30
• 33
• 35
• 38
• 42

1. 1. Find the median of the data set and label it “50th percentile.” This splits the data into an upper half and a lower half.

   2. Find the middle value of the lower half of the data, without including the median. Label this value “25th percentile.”

   3. Find the middle value of the upper half of the data, without including the median. Label this value “75th percentile.”

2. You have split the data set into four pieces. Each of the three values that split the data is called a quartile.

   • We call the 25th percentile the first quartile. Write “Q1” next to that number.
   • The median can be called the second quartile. Write “Q2” next to that number.
   • We call the 75th percentile the third quartile. Write “Q3” next to that number.

3. Label the lowest value in the set “minimum” and the greatest value “maximum.”

4. The values you have identified make up the five-number summary for the data set. Record them here.

   minimum: _____     Q1: _____     Q2: _____     Q3: _____     maximum: _____

5. The median of this data set is 20. This tells us that half of the people at the party were 20 years old or younger, and the other half were 20 or older. What do each of these other values tell us about the ages of the people at the party?

   1. the third quartile
   2. the minimum
   3. the maximum

Your teacher will give you the data on the lengths of names of students in your class. Write the five-number summary by finding the data set's minimum, Q1, Q2, Q3, and the maximum.

Pause for additional instructions from your teacher.

Twenty people participated in a study about blinking. The number of times each person blinked while watching a video for one minute was recorded. The data values are shown here, in order from smallest to largest.

• 3
• 6
• 8
• 11
• 11
• 13
• 14
• 14
• 14
• 14
• 16
• 18
• 20
• 20
• 20
• 22
• 24
• 32
• 36
• 51

1. 1. Use the grid and axis to make a dot plot of this data set.

      

      

   2. Find the median (Q2) and mark its location on the dot plot.
   3. Find the first quartile (Q1) and the third quartile (Q3). Mark their locations on the dot plot.

   4. What are the minimum and maximum values?

2. A box plot can be used to represent the five-number summary graphically. Let’s draw a box plot for the number-of-blinks data. On the grid, above the dot plot:

   1. Draw a box that extends from the first quartile (Q1) to the third quartile (Q3). Label the quartiles.
   2. At the median (Q2), draw a vertical line from the top of the box to the bottom of the box. Label the median.
   3. From the left side of the box (Q1), draw a horizontal line (a whisker) that extends to the minimum of the data set. On the right side of the box (Q3), draw a similar line that extends to the maximum of the data set.

3. You have now created a box plot to represent the number of blinks data. What fraction of the data values are represented by each of these elements of the box plot?

   1. The left whisker
   2. The box
   3. The right whisker

Earlier we learned that the mean is a measure of the center of a distribution and the MAD is a measure of the variability (or spread) that goes with the mean. There is also a measure of spread that goes with the median. It is called the interquartile range (IQR).

Finding the IQR involves splitting a data set into fourths. Each of the three values that splits the data into fourths is called a quartile.

• The median, or second quartile (Q2), splits the data into two halves.
• The first quartile (Q1) is the middle value of the lower half of the data.
• The third quartile (Q3) is the middle value of the upper half of the data. 

For example, here is a data set with 11 values.

• The median is 33.
• The first quartile is 20. It is the median of the numbers less than 33. 
• The third quartile 40. It is the median of the numbers greater than 33.

The difference between the maximum and minimum values of a data set is the range. The difference between Q3 and Q1 is the interquartile range (IQR). Because the distance between Q1 and Q3 includes the middle two-fourths of the distribution, the values between those two quartiles are sometimes called the middle half of the data.

The bigger the IQR, the more spread out the middle half of the data values are. The smaller the IQR, the closer together the middle half of the data values are. This is why we can use the IQR as a measure of spread.

A five-number summary can be used to summarize a distribution. It includes the minimum, first quartile, median, third quartile, and maximum of the data set. For the previous example, the five-number summary is 12, 20, 33, 40, and 49. These numbers are marked with diamonds on the dot plot.

Different data sets can have the same five-number summary. For instance, here is another data set with the same minimum, maximum, and quartiles as the previous example.

A box plot represents the five-number summary of a data set.

It shows the first quartile (Q1) and the third quartile (Q3) as the left and right sides of a rectangle or a box. The median (Q2) is shown as a vertical segment inside the box. On the left side, a horizontal line segment—a “whisker”—extends from Q1 to the minimum value. On the right, a whisker extends from Q3 to the maximum value.

The rectangle in the middle represents the middle half of the data. Its width is the IQR. The whiskers represent the bottom quarter and top quarter of the data set.

The box plots for these data sets are shown above the corresponding dot plots.

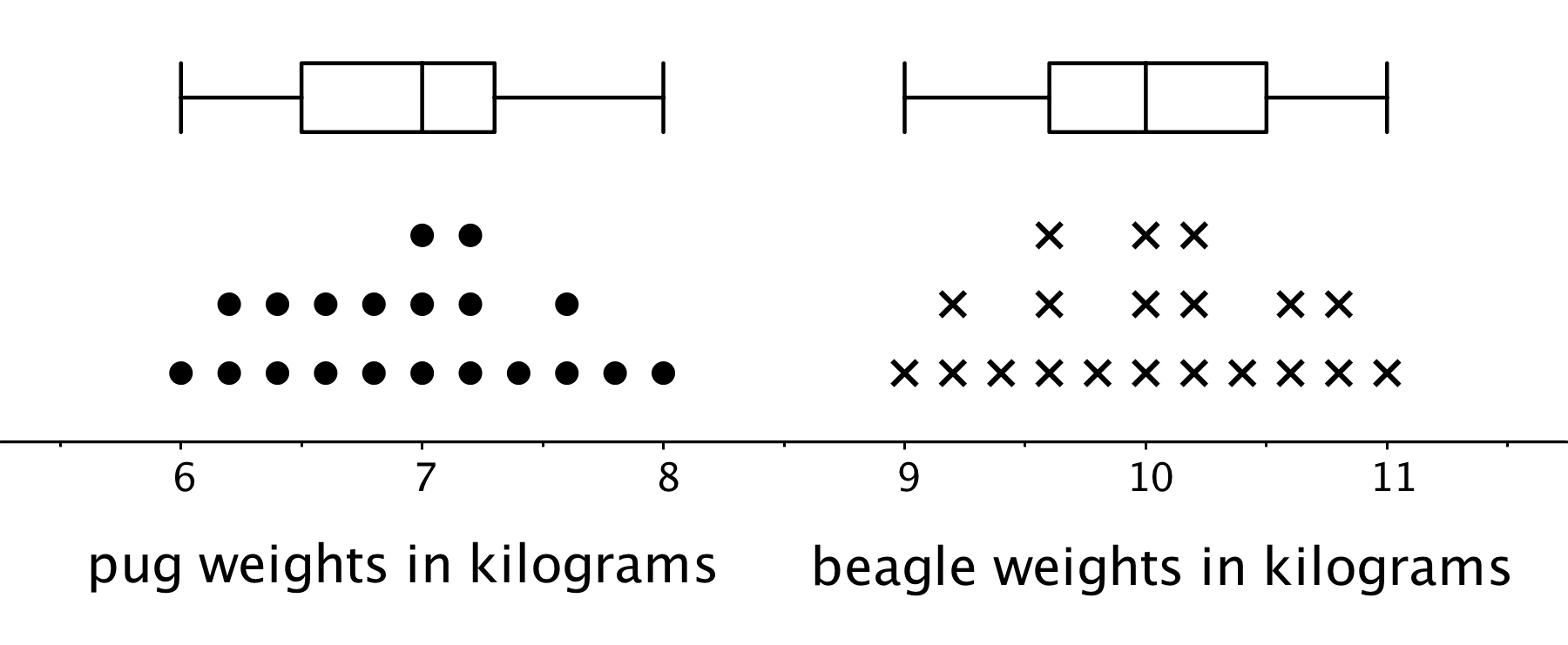
We can tell from the box plots that, in general, the pugs in the group are lighter than the beagles: the median weight of pugs is 7 kilograms and the median weight of beagles is 10 kilograms. Because the two box plots are on the same scale and the rectangles have similar widths, we can also tell that the IQRs for the two breeds are very similar. This suggests that the variability in the beagle weights is very similar to the variability in the pug weights.