Lesson 5
Reasoning About Square Roots
Problem 1
-
Explain how you know that \(\sqrt{37}\) is a little more than 6.
-
Explain how you know that \(\sqrt{95}\) is a little less than 10.
-
Explain how you know that \(\sqrt{30}\) is between 5 and 6.
Solution
For access, consult one of our IM Certified Partners.
Problem 2
Plot each number on the number line: \(\displaystyle 6, \sqrt{83}, \sqrt{40}, \sqrt{64}, 7.5\)
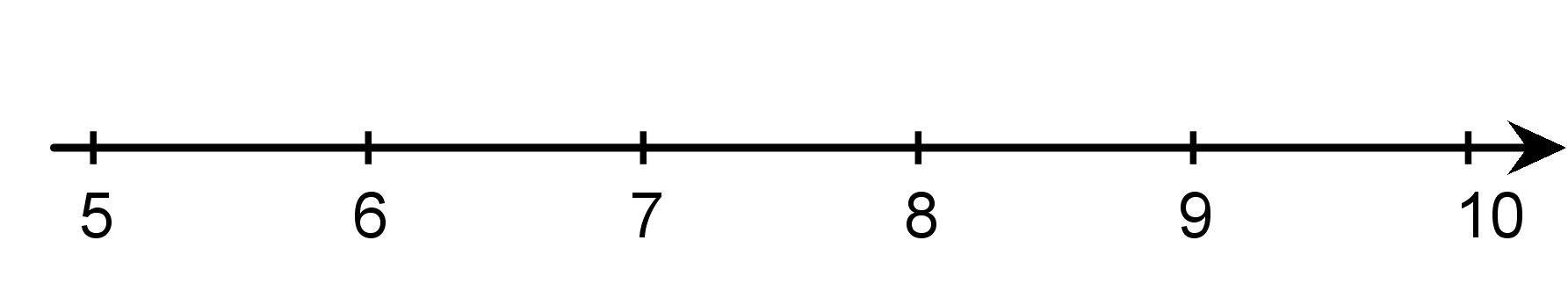
Solution
For access, consult one of our IM Certified Partners.
Problem 3
The equation \(x^2=25\) has two solutions. This is because both \(5 \boldcdot 5 = 25\), and also \(\text-5 \boldcdot \text-5 = 25\). So, 5 is a solution, and also -5 is a solution.
Select all the equations that have a solution of -4:
\(10+x=6\)
\(10-x=6\)
\(\text-3x=\text-12\)
\(\text-3x=12\)
\(8=x^2\)
\(x^2=16\)
Solution
For access, consult one of our IM Certified Partners.
Problem 4
Find all the solutions to each equation.
- \(x^2=81\)
- \(x^2=100\)
- \(\sqrt{x}=12\)
Solution
For access, consult one of our IM Certified Partners.
Problem 5
Select all the irrational numbers in the list. \(\displaystyle \frac23, \frac {\text{-}123}{45}, \sqrt{14}, \sqrt{64}, \sqrt\frac91, \text-\sqrt{99}, \text-\sqrt{100}\)
Solution
For access, consult one of our IM Certified Partners.
(From Unit 8, Lesson 3.)Problem 6
Each grid square represents 1 square unit. What is the exact side length of the shaded square?

Solution
For access, consult one of our IM Certified Partners.
(From Unit 8, Lesson 2.)Problem 7
For each pair of numbers, which of the two numbers is larger? Estimate how many times larger.
- \(0.37 \boldcdot 10^6\) and \(700 \boldcdot 10^4\)
- \(4.87 \boldcdot 10^4\) and \(15 \boldcdot 10^5\)
- \(500,000\) and \(2.3 \boldcdot 10^8\)
Solution
For access, consult one of our IM Certified Partners.
(From Unit 7, Lesson 10.)Problem 8
The scatter plot shows the heights (in inches) and three-point percentages for different basketball players last season.
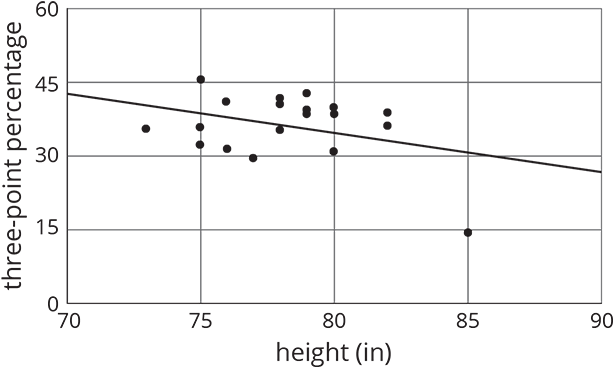
- Circle any data points that appear to be outliers.
- Compare any outliers to the values predicted by the model.
Solution
For access, consult one of our IM Certified Partners.
(From Unit 6, Lesson 4.)