Lesson 10
Applications of the Pythagorean Theorem
10.1: Closest Estimate: Square Roots (5 minutes)
Warm-up
The purpose of this warm-up is for students to reason about square roots by estimating the value of each expression. The values given as choices are close in range to encourage students to use the square roots they know to help them estimate ones they do not. These understandings will be helpful for students in upcoming activities where they will be applying the Pythagorean Theorem.
While four problems are given, it may not be possible to share every strategy. Consider gathering only two or three different strategies per problem.
Launch
Display one problem at a time. Give students 30 seconds of quiet think time for each problem and ask them to give a signal when they have an answer and a strategy. Keep all previous problems displayed throughout the talk. Follow with a whole-class discussion.
Student Facing
Which estimate is closest to the actual value of the expression? Explain your reasoning.
-
\(\sqrt{24}\)
-
4
-
4.5
-
5
-
-
\(\sqrt7\)
-
2
-
2.5
-
3
-
-
\(\sqrt{42}\)
-
6
-
6.5
-
7
-
-
\(\sqrt{10}\) + \(\sqrt{97}\)
-
13
-
13.25
-
13.5
-
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Ask students to share their strategies for each problem. Record and display their responses for all to see. After each student shares, ask if their chosen estimate is more or less than the actual value of each expression.
Design Principle(s): Optimize output (for explanation)
10.2: Cutting Corners (15 minutes)
Activity
The purpose of this activity is for students to use the Pythagorean Theorem to reason about distances and speeds to figure out who will win a race. Students must translate between the context and the geometric representation of the context and back (MP2). Identify students whose work is clearly labeled and organized to share during the whole-class discussion.
Launch
Arrange students in groups of 2. Provide students with access to calculators. Ask students to read and answer the first problem and then give a signal when they have done so. Next, poll the class to see who students think will win the race and post the results of the poll for all to see. Select 2–3 students to share why they chose who they chose. The conversation should illuminate a few key points: Mai travels farther than Tyler, but she is also going faster, so it is not immediately clear who will win.
Give 2 minutes of quiet work time for the second problem, followed by partner and then whole-class discussions.
Supports accessibility for: Language
Design Principle(s): Support sense-making
Student Facing
Mai and Tyler were standing at one corner of a large rectangular field and decided to race to the opposite corner. Since Mai had a bike and Tyler did not, they thought it would be a fairer race if Mai rode along the sidewalk that surrounds the field while Tyler ran the shorter distance directly across the field. The field is 100 meters long and 80 meters wide. Tyler can run at around 5 meters per second, and Mai can ride her bike at around 7.5 meters per second.
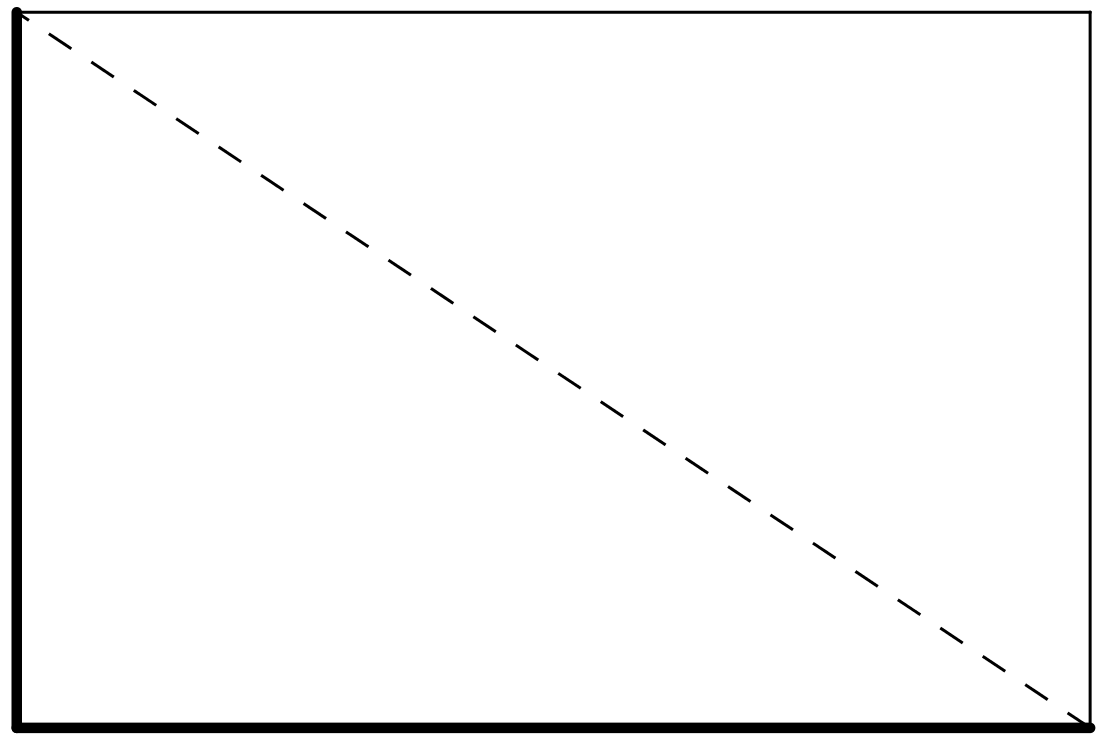
-
Before making any calculations, who do you think will win? By how much? Explain your thinking.
- Who wins? Show your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
A calculator may be necessary to answer the following questions. Round answers to the nearest hundredth.
-
If you could give the loser of the race a head start, how much time would they need in order for both people to arrive at the same time?
-
If you could make the winner go slower, how slow would they need to go in order for both people to arrive at the same time?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may rush through reading the problem and mix up who is traveling which path at what speed. Encourage these students to label the relevant distances and information on the diagram.
Activity Synthesis
The purpose of this discussion is for students to share how they organized their work for the problem and see how accurate students’ predictions at the start of the activity were. Select 1–2 previously identified students to share their work. Directly draw attention to how careful labeling of provided figures and organization of calculations when problems have multiple steps helps to both solve problems and identify errors. For example, in problems where multiple calculations are completed using a calculator, it is easy to copy an incorrect number, such as writing 14,600 instead of 16,400 for the sum \(100^2+80^2\).
10.3: Internal Dimensions (15 minutes)
Activity
The purpose of this task is for students to use the Pythagorean Theorem to calculate which rectangular prism has the longer diagonal length. To complete the activity, students will need to picture or sketch the right triangles necessary to calculate the diagonal length.
Identify groups using well-organized strategies to calculate the diagonals. For example, for Prism K some groups may draw in the diagonal on the bottom face of the cube and label it with an unknown variable, such as \(s\), to set up the calculation for the diagonal as \(\sqrt{6^2+s^2}\). Students would then know that to finish this calculation, they would need to find the value of \(s\), which is can be done using the edge lengths of the face of the prism \(s\) is drawn on.
The idea that the Pythagorean Theorem might be applied several times in order to find a missing length is taken even further in the extension, where students can apply it over a dozen times, hopefully noticing some repeated reasoning along the way, in order to find the last length.
Launch
Arrange students in groups of 2. Provide access to calculators. Ask students to read and consider the first problem and then give a signal when they have done so. If possible, use an actual rectangular prism, such as a small box, to help students understand what length the diagonal shows in the image. Once students understand what the first problem is asking, poll the class to see which prism they think has the longer diagonal and post the results of the poll for all to see. Select 2–3 students to share why they chose the prism they did. The conversation should illuminate a few key points: Prism K has one edge with length 6 units, which is longer than any of the edges of Prism L, but it also has a side of length 4 units, which is shorter than any of the edges of Prism L. Prism K also has a smaller volume than Prism L.
Give 1 minute of quiet think time for students to brainstorm how they will calculate the lengths of each diagonal. Ask partners to discuss their strategies before starting their calculations. Follow with a whole-class discussion.
Supports accessibility for: Visual-spatial processing; Conceptual processing
Design Principle(s): Maximize meta-awareness
Student Facing
Here are two rectangular prisms:
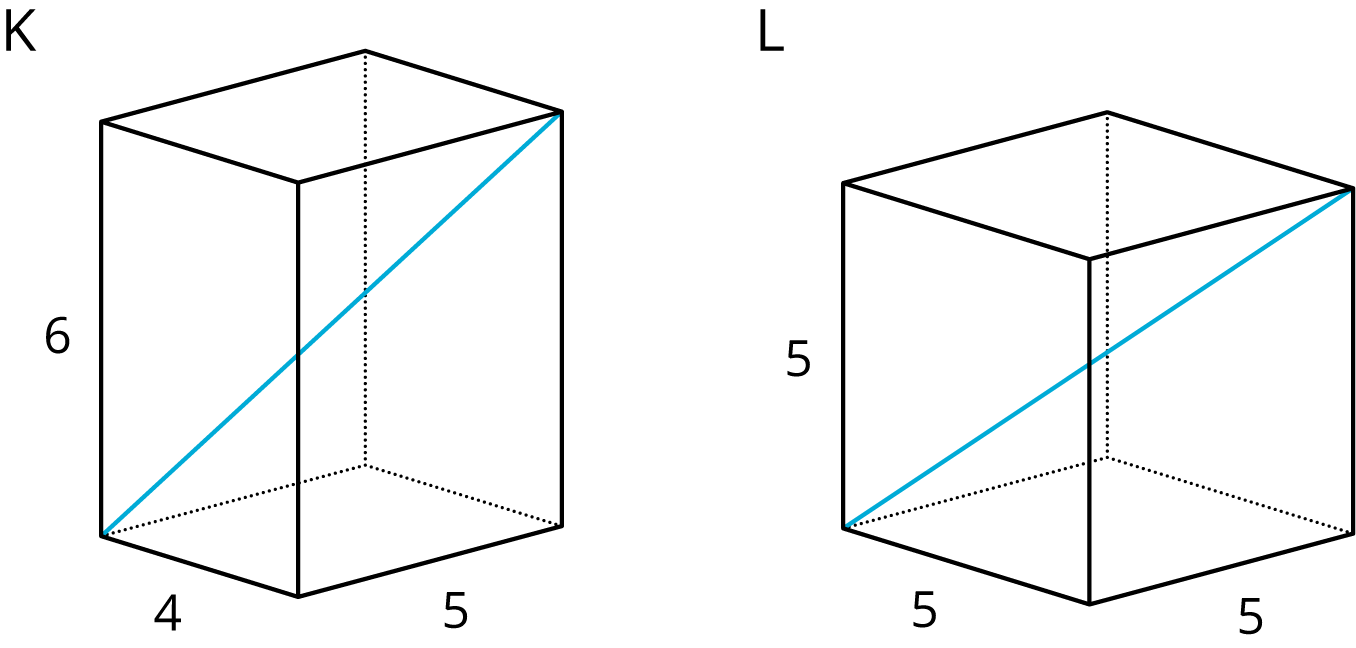
- Which figure do you think has the longer diagonal? Note that the figures are not drawn to scale.
- Calculate the lengths of both diagonals. Which one is actually longer?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Ask groups to share how they calculated the diagonal of one of the rectangular prisms. Display the figures in the activity for all to see and label the them while groups share.
If time allows and no groups pointed out how the diagonal length of the rectangular prisms are the square root of the sum of the squares of the three edge lengths, use Prism K and the calculations students shared to do so. For example, to calculate the diagonal of Prism K, students would have to calculate \(\sqrt{6^2+\left(\sqrt{41}\right)^2}\), but \(\sqrt{41}\) is from \(\sqrt{5^2+4^2}\) which means the diagonal length is really \(\sqrt{6^2+5^2+4^2}\) since \(\sqrt{6^2+\left(\sqrt{41}\right)^2}=\sqrt{6^2+\left(\sqrt{5^2+4^2}\right)^2}=\sqrt{6^2+5^2+4^2}\). So, for a rectangular prism with sides \(d\), \(e\), and \(f\), the length of the diagonal of the prism is just \(\sqrt{d^2+e^2+f^2}\).
Lesson Synthesis
Lesson Synthesis
Tell students that there are many situations in the world where we can use the Pythagorean Theorem to solve problems. Ask, “What situations that you can think of involve right triangles?” Give brief quiet think time, then invite students to share their ideas. For example, thick wires (called guy-wires) are used to keep telephone poles upright and their length depends on how high up the pole they attach and how far away from the pole they hook into the ground.
10.4: Cool-down - Jib Sail (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
The Pythagorean Theorem can be used to solve any problem that can be modeled with a right triangle where the lengths of two sides are known and the length of the other side needs to be found. For example, let’s say a cable is being placed on level ground to support a tower. It’s a 17-foot cable, and the cable should be connected 15 feet up the tower. How far away from the bottom of the tower should the other end of the cable connect to the ground?
It is often very helpful to draw a diagram of a situation, such as the one shown here:
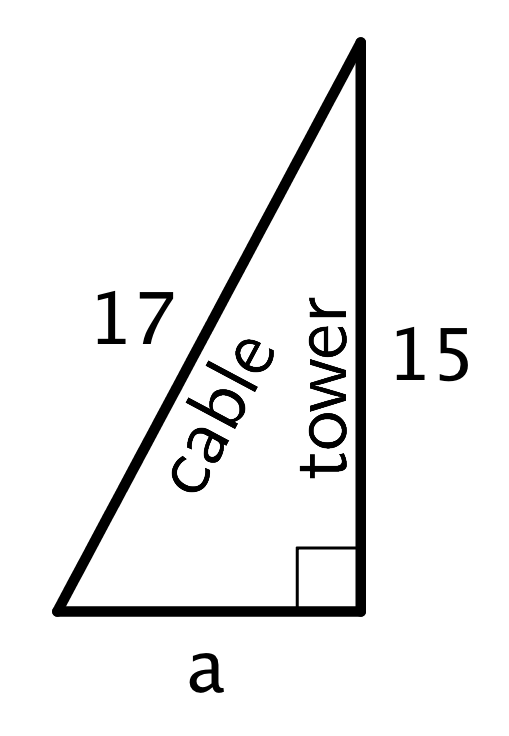
It’s assumed that the tower makes a right angle with the ground. Since this is a right triangle, the relationship between its sides is \(a^2+b^2=c^2\), where \(c\) represents the length of the hypotenuse and \(a\) and \(b\) represent the lengths of the other two sides. The hypotenuse is the side opposite the right angle. Making substitutions gives \(a^2+15^2=17^2\). Solving this for \(a\) gives \(a=8\). So, the other end of the cable should connect to the ground 8 feet away from the bottom of the tower.