Lesson 13

Write each number in scientific notation.

1. 14,700
2. 0.00083
3. 760,000,000
4. 0.038
5. 0.38
6. 3.8
7. 3,800,000,000,000
8. 0.0000000009

Perform the following calculations. Express your answers in scientific notation.

1. \((2 \times 10^5) + (6 \times 10^5)\)
    
2. \((4.1 \times 10^7) \boldcdot 2\)
    
3. \((1.5 \times 10^{11}) \boldcdot 3\)
    
4. \((3 \times 10^3)^2\)
    
5. \((9 \times 10^6) \boldcdot (3 \times 10^6)\)

Jada is making a scale model of the solar system. The distance from Earth to the Moon is about \(2.389 \times 10^5\) miles. The distance from Earth to the Sun is about \(9.296 \times 10^7\) miles. She decides to put Earth on one corner of her dresser and the Moon on another corner, about a foot away. Where should she put the sun?

• On a windowsill in the same room?
• In her kitchen, which is down the hallway?
• A city block away?

Explain your reasoning.

Here is the graph for one equation in a system of equations.

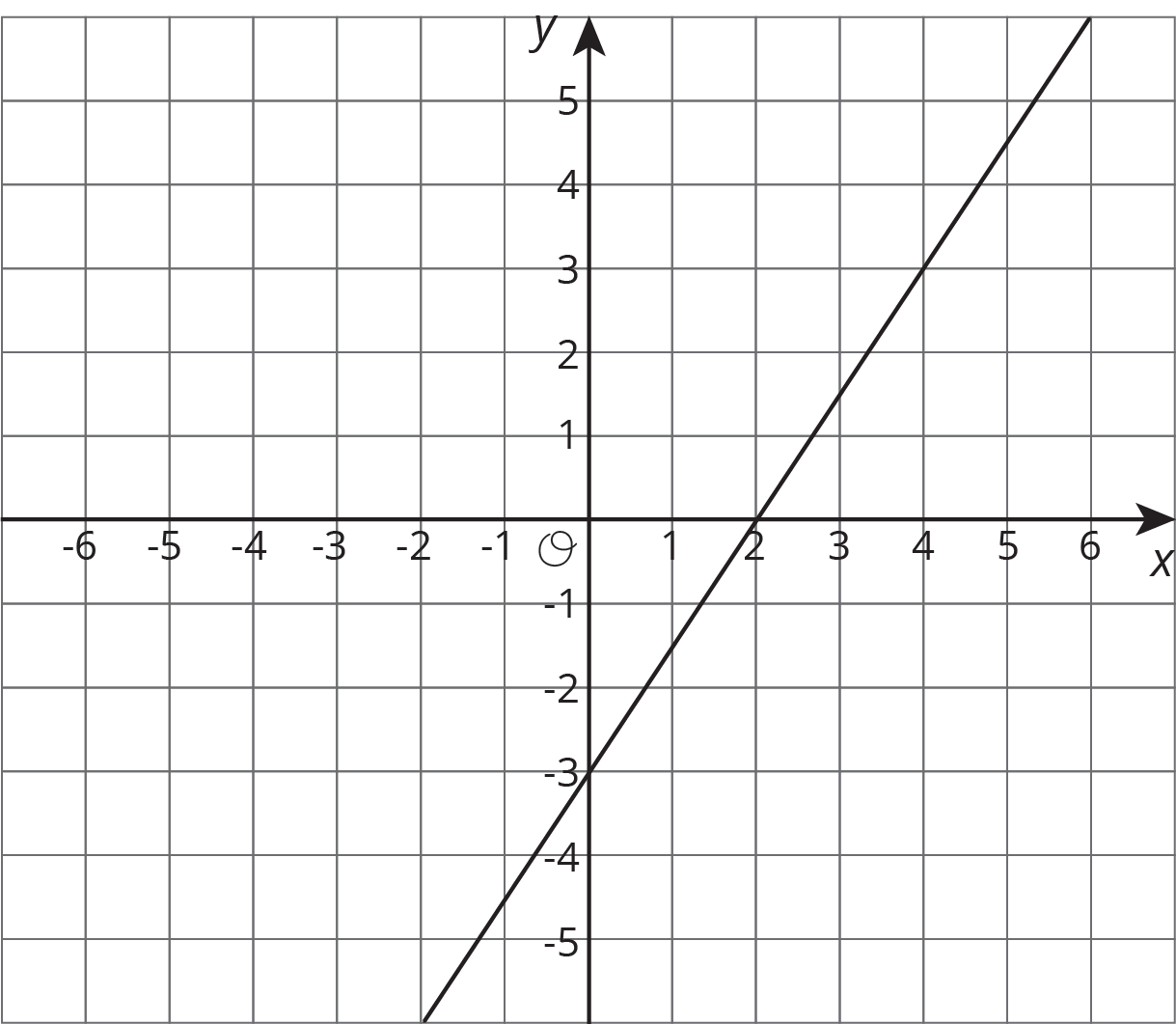
1. Write a second equation for the system so it has infinitely many solutions.
2. Write a second equation whose graph goes through \((0,2)\) so that the system has no solutions.
3. Write a second equation whose graph goes through \((2,2)\) so that the system has one solution at \((4,3)\).