Lesson 3
Powers of Powers of 10
3.1: Big Cube (5 minutes)
Warm-up
The purpose of this warm-up is to introduce students the idea of raising a value with an exponent to another power. Computing the volume of a cube whose side lengths are themselves powers of 10 introduces the basic structure of a power to a power, which will lead to a general exponent rule during later activities.
Look out for different strategies used to compute \(10,\!000^3\) so they can be discussed during whole-class discussion. Some students may count zeros to keep track of place value, while other students will write 10,000 as \(10^4\) and use exponent rules.
Launch
Give students 3 minutes of quiet work time followed by a brief whole-class discussion.
Student Facing
What is the volume of a giant cube that measures 10,000 km on each side?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may want to compute by multiplying \((10,\!000) \boldcdot (10,\!000) \boldcdot (10,\!000)\). Ask these students whether they can use powers of 10 and the exponent rule from the last lesson to make their calculations easier.
Activity Synthesis
The purpose of discussion is to highlight the fact that \(\left(10^4\right)^3\) is equal to \(10^{12}\) as a way to transition to the next activity, where this pattern is generalized. Select previously identified students to share their strategies for computing \(10,\!000^3\). Ask students what patterns they notice between \(\left(10^4\right)^3\) and \(10^{12}\). If students mention the strategy of counting zeros to multiply powers of 10, connect it to the process of adding exponents. In other words, the total volume in km3 is a 1 followed by the number of zeros in \((10,\!000) \boldcdot (10,\!000) \boldcdot (10,\!000)\) because \(10^4 \boldcdot 10^4 \boldcdot 10^4= 10^{4+4+4}\).
3.2: Raising Powers of 10 to Another Power (15 minutes)
Activity
Students explore patterns to discover the property \(\left( 10^m \right)^n = 10^{m \boldcdot n}\) for values of \(m\) and \(n\) that are positive integers. Non-positive integer exponents will be explored in a subsequent lesson. Notice students who try to rush to complete the table without recognizing the patterns moving between columns in the table. As students work, ask them if they can explain what patterns they are finding. Select students who can explain the patterns they see to share during whole-class discussion.
Launch
Give students 1 minute of quiet think time to complete the first unfinished row in the table, then select 1–2 students to share and explain their solutions. When it is clear that students know how to complete the table, explain to them that they can skip one entry in the table, but they have to be able to explain why they skipped it. Give students 10–12 minutes to work before a brief whole-class discussion.
Student Facing
-
-
Complete the table to explore patterns in the exponents when raising a power of 10 to a power. You may skip a single box in the table, but if you do, be prepared to explain why you skipped it.
expression expanded single power of 10 \((10^3)^2\) \((10 \boldcdot 10 \boldcdot 10)(10 \boldcdot 10 \boldcdot 10)\) \(10^6\) \((10^2)^5\) \((10 \boldcdot 10)(10 \boldcdot 10)(10 \boldcdot 10)(10 \boldcdot 10)(10 \boldcdot 10)\) \((10 \boldcdot 10 \boldcdot 10)(10 \boldcdot 10 \boldcdot 10)(10 \boldcdot 10 \boldcdot 10)(10 \boldcdot 10 \boldcdot 10)\) \((10^4)^2\) \((10^8)^{11}\) - If you chose to skip one entry in the table, which entry did you skip? Why?
-
- Use the patterns you found in the table to rewrite \(\left(10^m\right)^n\) as an equivalent expression with a single exponent, like \(10^{\boxed{\phantom{3}}}\).
- If you took the amount of oil consumed in 2 months in 2013 worldwide, you could make a cube of oil that measures \(10^3\) meters on each side. How many cubic meters of oil is this? Do you think this would be enough to fill a pond, a lake, or an ocean?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Select students who can explain the patterns they noticed to share in a whole-class discussion. Create a visual display for the rule \(\left(10^m\right)^n = 10^{m\boldcdot n}\) to display for all to see throughout the unit. For an example of how the rule works, consider showing \((10^2)^3 = (10 \boldcdot 10)(10 \boldcdot 10)(10 \boldcdot 10) = 10^6\) using colors or other visual aids to highlight that the result is \(10^6\) because there are three groups of \(10^2\). For example,
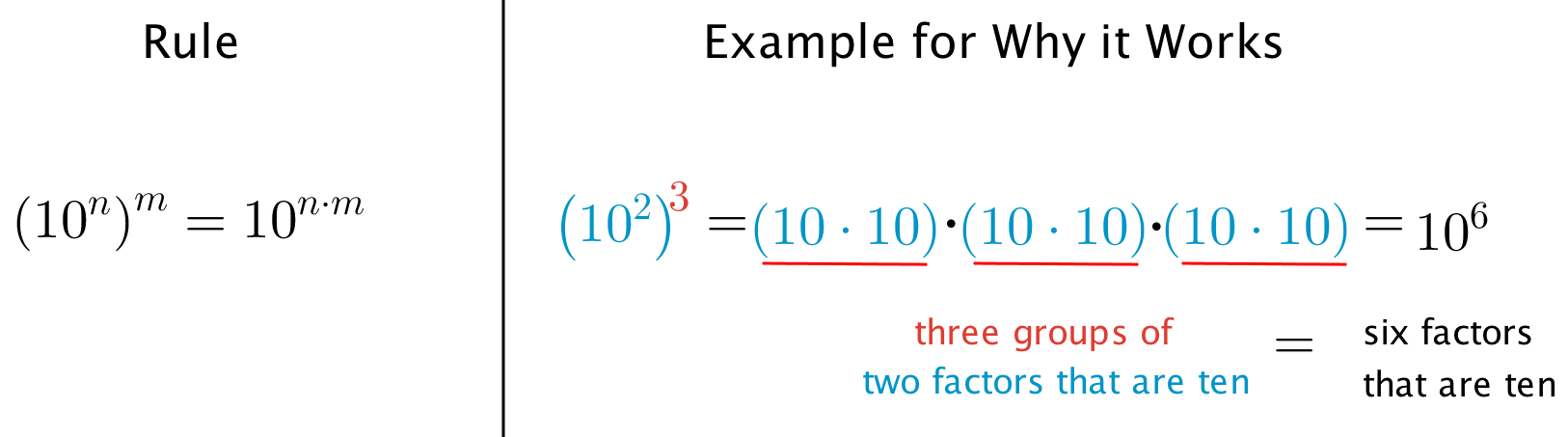
Design Principle(s): Optimize output (for explanation)
3.3: How Do the Rules Work? (10 minutes)
Activity
This activity presents two valid ways to write \(10^2 \boldcdot 10^2 \boldcdot 10^2\) with a single exponent, but where the execution of one of the ideas has a mistake. Thinking through this problem will reveal whether students understand the two exponent rules discussed in this lesson, providing opportunity for formative assessment.
Notice students who point out what was correct in both Andre and Elena’s responses. The eventual goal of learning exponent rules is to avoid expanding factors, but expect students at this stage to expand exponential expressions to test whether or not each step is correct.
Launch
Arrange students in groups of 2. Give 6–7 minutes to work followed by partner and whole-class discussions.
Supports accessibility for: Memory; Conceptual processing
Student Facing
Andre and Elena want to write \(10^2 \boldcdot 10^2 \boldcdot 10^2\) with a single exponent.
-
Andre says, “When you multiply powers with the same base, it just means you add the exponents, so \(10^2 \boldcdot 10^2 \boldcdot 10^2 = 10^{2+2+2} = 10^6\).”
-
Elena says, “\(10^2\) is multiplied by itself 3 times, so \(10^2 \boldcdot 10^2 \boldcdot 10^2 = (10^2)^3 = 10^{2+3} = 10^5\).”
Do you agree with either of them? Explain your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
\(2^{12} = 4,\!096\). How many other whole numbers can you raise to a power and get 4,096? Explain or show your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
It is important to note in the discussion that Elena is not completely wrong. She recognizes that \(10^2 \boldcdot 10^2 \boldcdot 10^2\) is equivalent to \((10^2)^3\), which shows good conceptual understanding of exponents as repeated multiplication. Select students to share any correct and incorrect steps that they and their partner noticed in Andre and Elena’s work. Ask students:
- “Andre wrote \(10^2 \boldcdot 10^2 \boldcdot 10^2 = 10^{2+2+2}\) and Elena wrote \(10^2 \boldcdot 10^2 \boldcdot 10^2 = (10^2)^3\). How are these ways of thinking different? How are they the same?” (Both methods are combining three powers using properties of exponents without writing out all of the factors. Andre’s method only considers the bases of the three powers to combine them while Elena’s method notices that each power is actually the same.)
- “What is one way you could avoid making the kinds of mistake that happened in this problem?” (Even if I don't write out all the factors, I could think about how many there will be if I were to write them out.)
Design Principle(s): Support sense-making; Optimize output (for explanation)
Lesson Synthesis
Lesson Synthesis
The purpose of the discussion is to check whether students understand why \(\left(10^n\right)^m = 10^{n \boldcdot m}\). Consider recording student responses and displaying them for all to see.
Here are some questions for discussion:
- “We looked at repeated multiplication of powers of 10. How would you write \(10^4 \boldcdot 10^4 \boldcdot 10^4\) with exponents instead of repeated multiplication?” (\(\left(10^4 \right)^3\))
- “Then how would you write \(\left(10^4 \right)^3\) using a single exponent?” (\(10^{12}\))
- “In general, why do you multiply the exponents when you write a power to a power with a single exponent? Give an example to show your reasoning.” (You multiply the exponents because the inner exponent shows how many factors are in each group and the outer exponent shows how many groups of factors there are. For example, \(\left(10^4\right)^3\) means that there are 3 groups of factors, and each group has 4 factors that are 10. So there are a total of \(3 \boldcdot 4 = 12\) factors that are 10 altogether.)
3.4: Cool-down - Making a Million (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
In this lesson, we developed a rule for taking a power of 10 to another power: Taking a power of 10 and raising it to another power is the same as multiplying the exponents. See what happens when raising \(10^4\) to the power of 3.
\(\left(10^4\right)^3 =10^4 \boldcdot 10^4 \boldcdot 10^4 = 10^{12}\)
This works for any power of powers of 10. For example, \(\left(10^{6}\right)^{11} = 10^{66}\). This is another rule that will make it easier to work with and make sense of expressions with exponents.