Lesson 2

This warm-up gives students a chance to think about different numbers that a diagram might represent. In later activities, students thinking about diagrams that represent different powers of 10.

Give students 1 minute of quiet think time followed by 2 minutes of partner discussion.

Poll the class to see who agrees with each person in turn. Then ask someone to explain in each case.

The purpose of this activity is for students to develop a sense of visual scale between powers of 10. Students should understand that multiplying by 10 corresponds to increasing the exponent by 1. Even though the notation for \(10^{100}\) does not appear to be much different than \(10^{98}\), it is 100 times larger. Small changes in the exponent can result in large changes in the value of the expression.

Arrange students in groups of 2. Give students 5 minutes of quiet work time followed by 5 minutes to share their responses with their partner and a whole-class discussion. 

Students may multiply the exponent by 10, for example \(10^2\), \(10^{20}\), \(10^{200}\). Ask these students to write out what \(10^{20}\) would mean and whether that matches their intention.

The key takeaway is that increasing the exponent of a power of 10 by 1 corresponds to multiplying or dividing by 10, and decreasing the exponent by 1 corresponds to dividing by 10.

Ask students to share their responses for the last several questions. Record and display their responses for all to see. If possible, reference the image to highlight the magnitude of change when the power of 10 increases or decreases by 1 or 2. If a student gives an answer such as, “the area of the medium rectangle is \(10^2 + 10^2 +.... + 10^2\), ask for volunteers to help write the expression using a single power of 10.

If projection is available, consider sharing this applet, which illustrates animals measured in units that vary by powers of ten. https://ggbm.at/NhpASDzz

The goal of this activity is to help students flexibly transition between different notations for powers of 10 and introduce the property of multiplication of values with the same base. Students observe that \(10^n \boldcdot 10^m = 10^{n+m}\) for values of \(n\) and \(m\) that are positive integers. The second question hints at the reasoning that will extend exponent rules to include zero exponents, but students will investigate that more deeply in a later lesson.

Notice students who need help writing the general rule in in terms of \(n\) and \(m\). You might ask, “What patterns did you notice with the exponents in the table? So if the exponents are \(n\) and \(m\), how do you write what you did with the exponents?”

Give students 1 minute of quiet think time to complete the first unfinished row in the table before asking 1–2 students to share and explain their answers. When it is clear that students know how to complete the table, explain to them that they can skip one entry in the table, but they have to be able to explain why they skipped it. Give students 7–8 minutes to work before a brief whole-class discussion.

Create and post visual displays showing the exponent rules for reference throughout the unit, with one visual display for each rule. The visual display could include an example to illustrate how the rule works, along with visual aids and use of color. Here is a sample visual display:

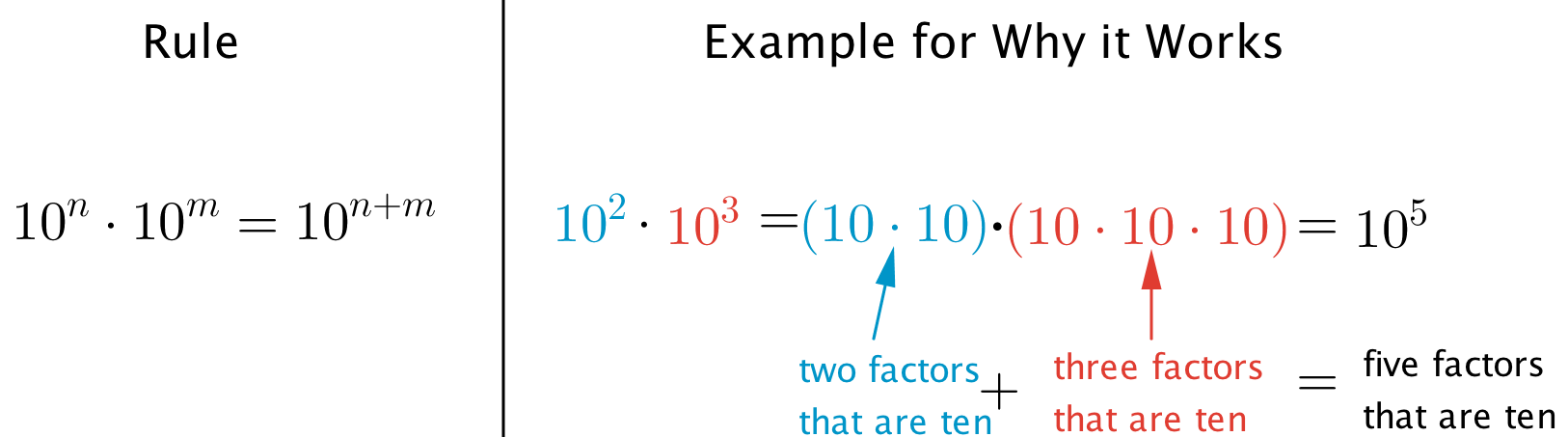
Explain the visual display to students and display it for all to see throughout the unit.