Lesson 13
Definition of Scientific Notation
Let’s use scientific notation to describe large and small numbers.
13.1: Number Talk: Multiplying by Powers of 10
Find the value of each expression mentally.
\(123 \boldcdot 10,\!000\)
\((3.4) \boldcdot 1,\!000\)
\((0.6) \boldcdot 100\)
\((7.3) \boldcdot (0.01)\)
13.2: The “Science” of Scientific Notation
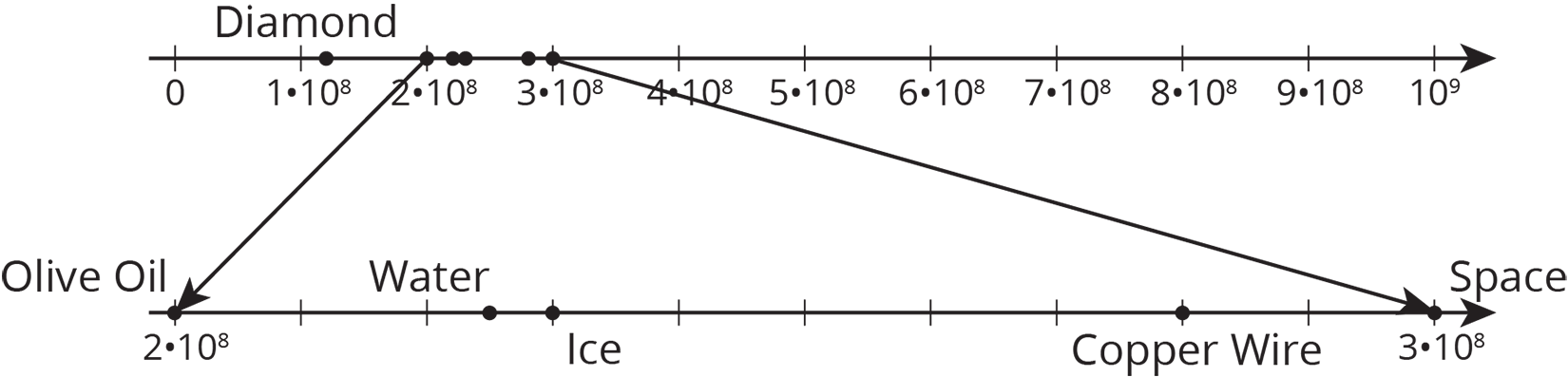
The table shows the speed of light or electricity through different materials.
| material | speed (meters per second) |
|---|---|
| space | 300,000,000 |
| water | \(2.25 \times 10^8\) |
| copper (electricity) | 280,000,000 |
| diamond | \(124 \times 10^6\) |
| ice | \(2.3 \times 10^8\) |
| olive oil | \(0.2 \times 10^9\) |
Circle the speeds that are written in scientific notation. Write the others using scientific notation.
13.3: Scientific Notation Matching
Your teacher will give you and your partner a set of cards. Some of the cards show numbers in scientific notation, and other cards show numbers that are not in scientific notation.
-
Shuffle the cards and lay them facedown.
-
Players take turns trying to match cards with the same value.
-
On your turn, choose two cards to turn faceup for everyone to see. Then:
-
If the two cards have the same value and one of them is written in scientific notation, whoever says “Science!” first gets to keep the cards, and it becomes that player’s turn. If it’s already your turn when you call “Science!”, that means you get to go again. If you say “Science!” when the cards do not match or one is not in scientific notation, then your opponent gets a point.
-
If both partners agree the two cards have the same value, then remove them from the board and keep them. You get a point for each card you keep.
-
If the two cards do not have the same value, then set them facedown in the same position and end your turn.
-
-
If it is not your turn:
-
If the two cards have the same value and one of them is written in scientific notation, then whoever says “Science!” first gets to keep the cards, and it becomes that player’s turn. If you call “Science!” when the cards do not match or one is not in scientific notation, then your opponent gets a point.
-
Make sure both of you agree the cards have the same value.
If you disagree, work to reach an agreement.
-
-
Whoever has the most points at the end wins.
- What is \(9 \times 10^{\text-1} + 9 \times 10^{\text-2}\)? Express your answer as:
- A decimal
- A fraction
- A decimal
- What is \(9 \times 10^{\text-1} + 9 \times 10^{\text-2} + 9 \times 10^{\text-3} +9 \times 10^{\text-4}\)? Express your answer as:
- A decimal
- A fraction
- A decimal
- The answers to the two previous questions should have been close to 1. What power of 10 would you have to go up to if you wanted your answer to be so close to 1 that it was only \(\frac{1}{1,000,000}\) off?
- What power of 10 would you have to go up to if you wanted your answer to be so close to 1 that it was only \(\frac{1}{1,000,000,000}\) off? Can you keep adding numbers in this pattern to get as close to 1 as you want? Explain or show your reasoning.
- Imagine a number line that goes from your current position (labeled 0) to the door of the room you are in (labeled 1). In order to get to the door, you will have to pass the points 0.9, 0.99, 0.999, etc. The Greek philosopher Zeno argued that you will never be able to go through the door, because you will first have to pass through an infinite number of points. What do you think? How would you reply to Zeno?
Summary
The total value of all the quarters made in 2014 is 400 million dollars. There are many ways to express this using powers of 10. We could write this as \(400 \boldcdot 10^6\) dollars, \(40 \boldcdot 10^7\) dollars, \(0.4 \boldcdot 10^9\) dollars, or many other ways. One special way to write this quantity is called scientific notation. In scientific notation,
400 million
dollars would be written as \(\displaystyle 4 \times 10^8\) dollars. For scientific notation, the \(\times\) symbol is the standard way to show multiplication instead of the \(\boldcdot \) symbol. Writing the number this way shows exactly where it lies between two consecutive powers of 10. The \(10^8\) shows us the number is between \(10^8\) and \(10^9\). The 4 shows us that the number is 4 tenths of the way to \(10^9\).
Some other examples of scientific notation are \(1.2 \times 10^{\text-8}\), \(9.99 \times 10^{16}\), and \(7 \times 10^{12}\). The first factor is a number greater than or equal to 1, but less than 10. The second factor is an integer power of 10.
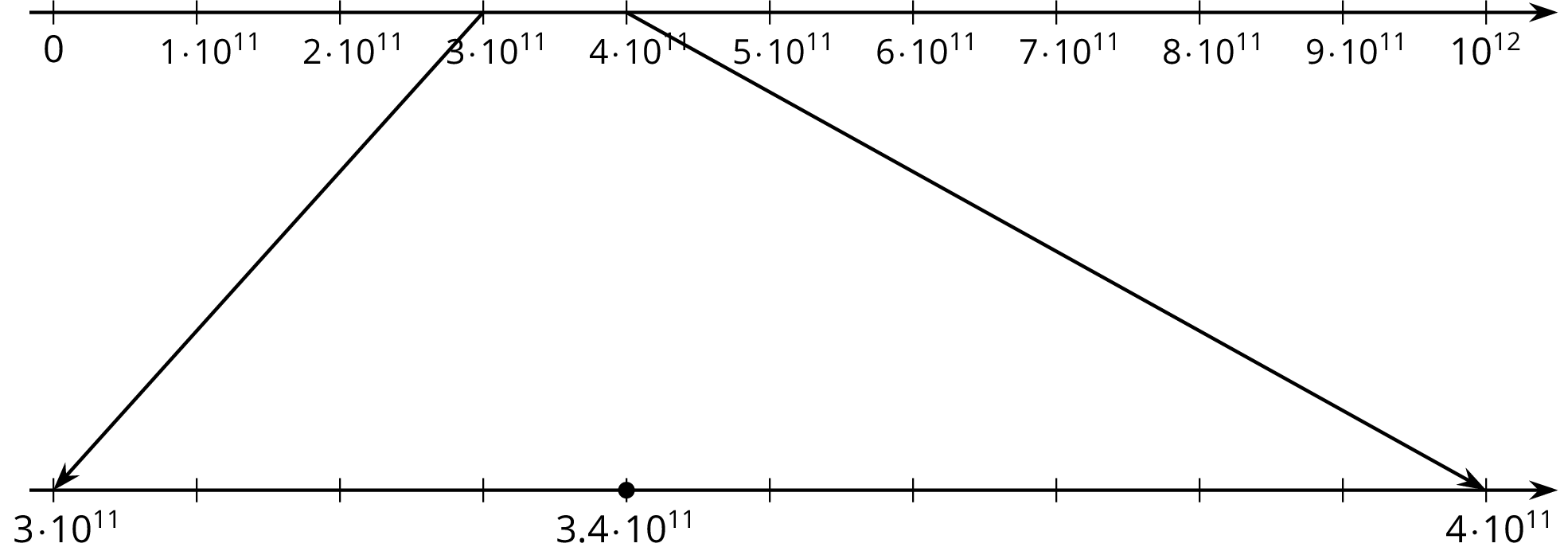
Thinking back to how we plotted these large (or small) numbers on a number line, scientific notation tells us which powers of 10 to place on the left and right of the number line. For example, if we want to plot \(3.4 \times 10^{11}\) on a number line, we know that the number is larger than \(10^{11}\), but smaller than \(10^{12}\). We can find this number by zooming in on the number line:
Glossary Entries
- scientific notation
Scientific notation is a way to write very large or very small numbers. We write these numbers by multiplying a number between 1 and 10 by a power of 10.
For example, the number 425,000,000 in scientific notation is \(4.25 \times 10^8\). The number 0.0000000000783 in scientific notation is \(7.83 \times 10^{\text-11}\).