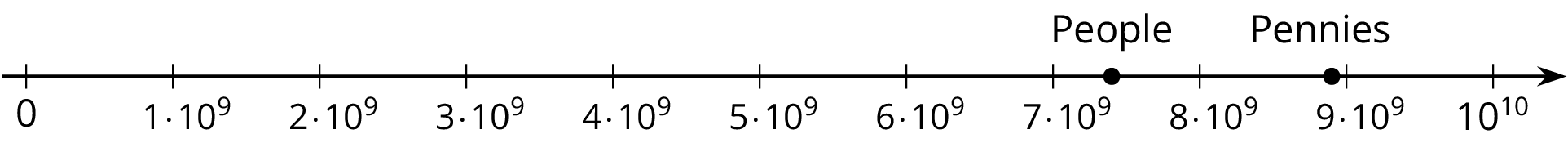Lesson 10
Representing Large Numbers on the Number Line
10.1: Labeling Tick Marks on a Number Line (5 minutes)
Warm-up
This warm-up prompts students to reason about values on a number line that end in a power of 10. It enables them to visualize and make sense of numbers expressed as a product of a single digit and a power of 10, which prepares them to begin working with scientific notation.
Expect student responses to include a variety of incorrect or partially-correct ideas. It is not important that all students understand the correct notation at this point, so it is not necessary to extend the time for this reason.
During the partner discussions, identify and select students who have partially-correct responses to share during the whole-class discussion.
Launch
Arrange students in groups of 2. Give students 1 minute of quiet work time and then 2 minutes to compare their number line with their partner. Tell the partners to try and come to an agreement on the values on the number line. Follow with a whole-class discussion.
Student Facing
Label the tick marks on the number line. Be prepared to explain your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
- Some students may count the tick marks instead of the segments and think \(10^7\) is being divided into 9 or 11 parts. Consider asking these students to mark each segment with a highlighter to count them.
- Some students may try to label the tick marks \(10^1\), \(10^2\), \(10^3\), etc., and as a result, they may say that the \(10^7\) is shown in the wrong place. Ask these students how many equal parts \(10^7\) is divided into, and how they would write that as a division problem or with a fraction.
- Some students may label the tick marks as \(10^6\), \(20^6\), \(30^6\), etc. Ask these students to expand \(20^6\) and \(10^6\) into their repeated factors and compare them so they see that \(20^6\) is not twice as much as \(10^6\).
- Some students may work with the idea of \(\frac{1}{2}\) and label the middle tick mark as \(10^{3.5}\). Explain that this tick mark would have a value of \(\frac12 \boldcdot 10^7\) and ask these students to use what they know about powers of 10 to find the value of the first tick mark after 0.
Activity Synthesis
Ask selected students to explain how they labeled the number line. Record and display their responses on the number line for all to see. As students share, use their responses, correct or incorrect, to guide students to the idea that the first tick mark is \(1 \boldcdot 10^6\), the second is \(2 \boldcdot 10^6\), etc. This gives students the opportunity to connect the number line representation with the computational rules they developed in previous lessons. For example, if a student claims that the second tick mark is \(20^6\), they can check whether \(20^6\) is equal to \(2 \boldcdot 10^6\) by expanding both expressions.
If not uncovered in students' explanations, ask the following questions to make sure students see how to label the number line correctly:
- “How many equal parts is \(10^7\) being divided into?” (10)
- “If the number at the end of this number line were 20, how would we find the value of each tick mark?” (Divide 20 by 10)
- “Can we use the same reasoning with \(10^7\) at the end?” (Yes)
- “What is \(10^7 \div 10\)?” (\(10^6\)) “What does this number represent?” (The distance between two tick marks)
- “Can we write \(10^6\) as \(1 \boldcdot 10^6\)?” (Yes).
- “If the first tick mark is \(1 \boldcdot 10^6\), then what is the second tick mark?” (\(2 \boldcdot 10^6\)) “
10.2: Comparing Large Numbers with a Number Line (10 minutes)
Activity
This activity encourages students to use the number line to make sense of powers of 10 and think about how to rewrite expressions in the form \(b \boldcdot 10^n\), where \(b\) is between 1 and 10 (as in the case of scientific notation). It prompts students to use the structure of the number line to compare numbers, and to extend their use to estimate relative sizes of other numbers when no number lines are given.
As students work, notice the ways in which they compare expressions that are not written as multiples of \(10^6\). Highlight some of these methods in the discussion.
Launch
Arrange students in groups of 2. Give students 4 minutes of quiet time to work on the first problem, followed by 1–2 minutes to exchange and discuss their work with their partner (second problem).
Then, tell students that representing numbers as a single digit times a power of 10 is useful for making rough comparisons. Give an example: \(9 \boldcdot 10^{11}\) is roughly 200 times as large as \(4\boldcdot 10^9\), because \(10^{11}\) is 100 times as much as \(10^9\), and 9 is roughly twice as much as 4. Give students the remaining time to answer the last question. Follow with a brief whole-class discussion.
Classes using the digital version have an interactive applet. Students need to drag the points, marked with open circles and their coordinates, to their proper places on the number line. When all five points are on the line, feedback is available. Note: labels are placed above or below the points only to avoid crowding on the number line.
Supports accessibility for: Memory; Conceptual processing
Student Facing
- Drag the points to their proper places on the number line. Be prepared to explain your reasoning.
-
Discuss with a partner how you decided where each point should go.
- Which is larger, 4,000,000 or \(75 \boldcdot 10^5\)? Estimate how many times larger.
Student Response
For access, consult one of our IM Certified Partners.
Launch
Arrange students in groups of 2. Give students 4 minutes of quiet time to work on the first problem, followed by 1–2 minutes to exchange and discuss their work with their partner (second problem).
Then, tell students that representing numbers as a single digit times a power of 10 is useful for making rough comparisons. Give an example: \(9 \boldcdot 10^{11}\) is roughly 200 times as large as \(4\boldcdot 10^9\), because \(10^{11}\) is 100 times as much as \(10^9\), and 9 is roughly twice as much as 4. Give students the remaining time to answer the last question. Follow with a brief whole-class discussion.
Classes using the digital version have an interactive applet. Students need to drag the points, marked with open circles and their coordinates, to their proper places on the number line. When all five points are on the line, feedback is available. Note: labels are placed above or below the points only to avoid crowding on the number line.
Supports accessibility for: Memory; Conceptual processing
Student Facing
-
Place the numbers on the number line. Be prepared to explain your reasoning.
-
4,000,000
-
\(5 \boldcdot 10^6\)
-
\(5 \boldcdot 10^5\)
-
\(75 \boldcdot 10^5\)
-
\((0.6) \boldcdot 10^7\)
-
-
Trade number lines with a partner, and check each other’s work. How did your partner decide how to place the numbers? If you disagree about a placement, work to reach an agreement.
- Which is larger, 4,000,000 or \(75 \boldcdot 10^5\)? Estimate how many times larger.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Some students may misplace expressions like \((0.6) \boldcdot 10^7\) or \(75 \boldcdot 10^5\) on the number line. For \(75 \boldcdot 10^5\), point out that 75 is the same as \((7.5) \boldcdot 10\), so \(75 \boldcdot 10^5\) is equivalent to \((7.5) \boldcdot 10 \boldcdot 10^5\). For \((0.6) \boldcdot 10^7\), point out that 0.6 is the same as \(6 \boldcdot 10^{\text-1}\), so \((0.6) \boldcdot 10^7\) is equivalent to \(6 \boldcdot 10^{\text-1} \boldcdot 10^7\). Alternatively, tell the student to think of \((0.6) \boldcdot 10^7\) as between 0 and \(10^7\) in the same way that 0.6 is between 0 and 1 to guide them to the correct placement on the number line.
Activity Synthesis
Ask students, “How could you change 4,000,000, \(75 \boldcdot 10^5\), and \((0.6) \boldcdot 10^7\) so that all the expressions have the same power of 10?” Highlight the main idea that it’s always possible to rewrite an expression that is a multiple of a power of 10 so that the leading factor is between 1 and 10. For example, 75 can be written as \((7.5) \boldcdot 10\), and 0.6 can be written as \(6 \boldcdot 10^{\text-1}\).
If time allows, consider presenting a problem that allows students to use powers of 10 to estimate the relative sizes of large numbers and use them to answer a question in context:
- The population of the United States is roughly \(3 \boldcdot 10^8\) people. The global population is roughly \(7 \boldcdot 10^9\) people. Estimate how many times larger the global population is than the U.S. population. (\(7 \boldcdot 10^9\) is roughly 20 times as large as \(3 \boldcdot 10^8\), because 7 is roughly twice as large as 3, and \(10^9\) is 10 times as large as \(10^8\).)
Design Principle(s): Optimize output (for explanation)
10.3: The Speeds of Light (20 minutes)
Activity
This activity guides students to thinking in terms of scientific notation while investigating the properties of light. A number line that shows a power of 10 partitioned into 10 equal intervals is again used to illustrate the base-ten structure. Plotting numbers along it gives a clearer meaning to expressions that are a product of a single digit and a power of 10.
To distinguish more easily between the different speeds of light through various materials, the interval between \(2 \boldcdot 10^8\) and \(3 \boldcdot 10^8\) is magnified on the number line. This illustrates numbers with more decimal places and allows students to see how they are expressed in scientific notation.
Once a number line is labeled with powers of 10 and its structure is understood, numbers given in scientific notation can be placed on the number line fairly straightforwardly. This encourages students to look for ways to write the other numbers in scientific notation.
Launch
Display the following number line for all to see. Explain to students that as light moves through different materials, it slows down. The speed of light through empty space, with nothing in its way, is roughly 300,000,000 meters per second. The speed of light through olive oil is much slower at roughly 200,000,000 meters per second.
Ask students to decide what the power of 10 to use for the label of the rightmost tick mark on the number line so that the speed of light through space and through olive oil can be plotted. Give 1 minute of quiet think time before asking 1–2 students to share their responses. Make sure students see that \(10^9\) is appropriate because for 200,000,000 (which is \(2 \boldcdot 10^8\)) to be plotted between 0 and the last tick mark, the last power of 10 needs to be greater than \(10^8\)).

Next, give students 10–12 minutes to work followed by a whole-class discussion.
Students using the digital materials can use the applet to plot the numbers. The magnifying glass allows them to zoom into any interval between two tick marks and plot numbers to an additional decimal place.
Design Principle(s): Maximize meta-awareness; Support sense-making
Student Facing
The table shows how fast light waves or electricity can travel through different materials:
| material | speed of light (meters per second) |
|---|---|
| space | 300,000,000 |
| water | \((2.25) \boldcdot 10^8\) |
| copper wire (electricity) | 280,000,000 |
| diamond | \(124 \boldcdot 10^6\) |
| ice | \((2.3) \boldcdot 10^8\) |
| olive oil | 200,000,000 |
-
Which is faster, light through diamond or light through ice? How can you tell from the expressions for speed?
Let’s zoom in to highlight the values between \((2.0) \boldcdot 10^8\) and \((3.0) \boldcdot 10^8\).
-
Plot a point for each speed on both number lines, and label it with the corresponding material.
-
There is one speed that you cannot plot on the bottom number line. Which is it? Plot it on the top number line instead.
- Which is faster, light through ice or light through diamond? How can you tell from the number line?
Student Response
For access, consult one of our IM Certified Partners.
Launch
Display the following number line for all to see. Explain to students that as light moves through different materials, it slows down. The speed of light through empty space, with nothing in its way, is roughly 300,000,000 meters per second. The speed of light through olive oil is much slower at roughly 200,000,000 meters per second.
Ask students to decide what the power of 10 to use for the label of the rightmost tick mark on the number line so that the speed of light through space and through olive oil can be plotted. Give 1 minute of quiet think time before asking 1–2 students to share their responses. Make sure students see that \(10^9\) is appropriate because for 200,000,000 (which is \(2 \boldcdot 10^8\)) to be plotted between 0 and the last tick mark, the last power of 10 needs to be greater than \(10^8\)).

Next, give students 10–12 minutes to work followed by a whole-class discussion.
Students using the digital materials can use the applet to plot the numbers. The magnifying glass allows them to zoom into any interval between two tick marks and plot numbers to an additional decimal place.
Design Principle(s): Maximize meta-awareness; Support sense-making
Student Facing
The table shows how fast light waves or electricity can travel through different materials.
| material | speed (meters per second) |
|---|---|
| space | 300,000,000 |
| water | \((2.25) \boldcdot 10^8\) |
| copper wire (electricity) | 280,000,000 |
| diamond | \(124 \boldcdot 10^6\) |
| ice | \((2.3) \boldcdot 10^8\) |
| olive oil | 200,000,000 |
-
Which is faster, light through diamond or light through ice? How can you tell from the expressions for speed?
Let’s zoom in to highlight the values between \((2.0) \boldcdot 10^8\) and \((3.0) \boldcdot 10^8\).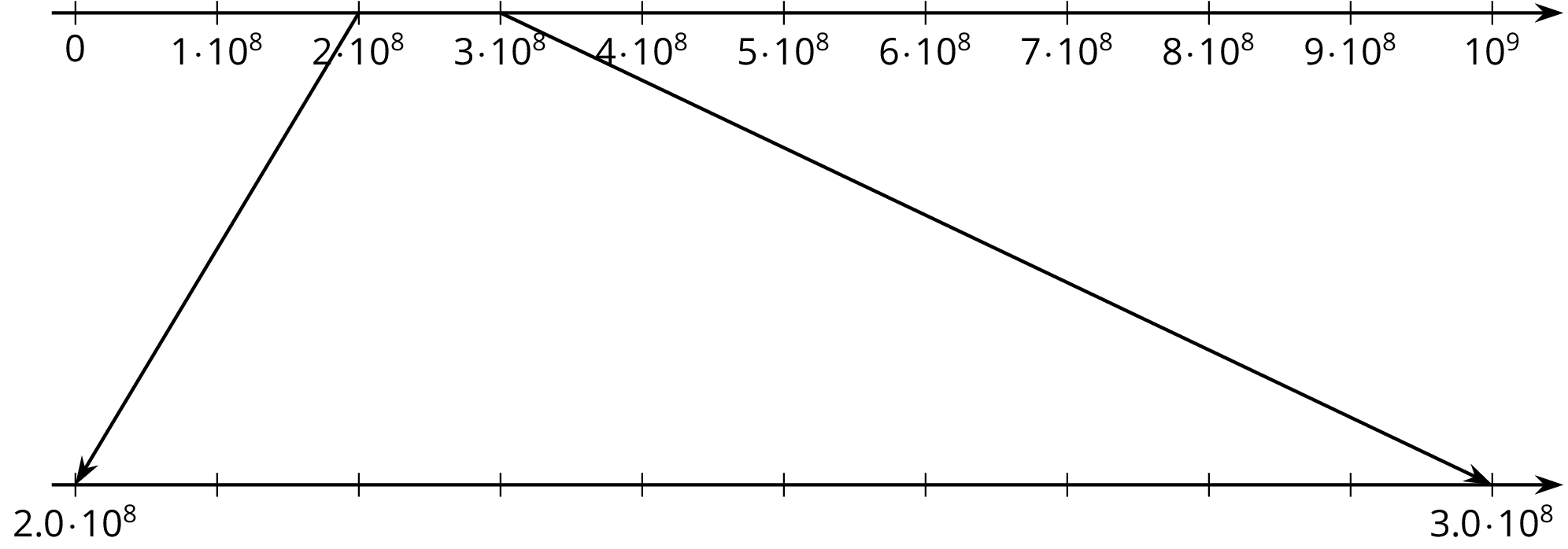
-
Label the tick marks between \((2.0) \boldcdot 10^8\) and \((3.0) \boldcdot 10^8\).
-
Plot a point for each speed on both number lines, and label it with the corresponding material.
- There is one speed that you cannot plot on the bottom number line. Which is it? Plot it on the top number line instead.
- Which is faster, light through ice or light through diamond? How can you tell from the number line?
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
Find a four-digit number using only the digits 0, 1, 2, or 3 where:
- the first digit tells you how many zeros are in the number,
- the second digit tells you how many ones are in the number,
- the third digit tells you how many twos are in the number, and
- the fourth digit tells you how many threes are in the number.
The number 2,100 is close, but doesn’t quite work. The first digit is 2, and there are 2 zeros. The second digit is 1, and there is 1 one. The fourth digit is 0, and there are no threes. But the third digit, which is supposed to count the number of 2’s, is zero.
- Can you find more than one number like this?
- How many solutions are there to this problem? Explain or show your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may struggle to rewrite a number written using one power of 10 as a number with a different power, for example writing \(125 \boldcdot 10^6\) using \(10^8\). Some may know the relationship between the powers of 10 (say, between \(10^6\) and \(10^8\)), but may not know how expressing one in terms of the other affects the other factor. Help students make sense of the rewriting process with a series of questions such as these:
- “What do we need to multiply \(10^6\) by to get \(10^8\)?” (100 or \(10^2\))
- “If we multiply \(10^6\) by \(10^2\), what must we also do to maintain the value of the expression? (Divide the other factor in the expression by \(10^2\).)
- “What is the resulting expression?” (\((125 \div 10^2) \boldcdot (10^6 \boldcdot 10^2) = (1.25) \boldcdot 10^8\))
- “How do we know that the two expressions are equivalent?” (We multiplied the expression by \(10^2\) and then divided it by \(10^2\), which is equal to multiplying it by 1.)
Activity Synthesis
Ask students to explain how they were able to compare the speeds of light. Students do not yet know the definition of scientific notation, but this activity should help them see that expressing values in this format allows us to more easily compare them. Consider using the applet to further illustrate how each number could be plotted on the number line.
Tell students, “We saw that the speed of light through ice can be written as \((2.3) \boldcdot 10^8\) meters per second, and the speed of electricity can be written as \((2.8) \boldcdot 10^8\) meters per second. When you write them both the same way like this, it makes it much easier to compare them.”
Lesson Synthesis
Lesson Synthesis
The purpose of the discussion is to check that students understand how to express a large number as a multiple of a power of 10, find the value of a given multiple of a power of 10, and compare different large numbers by expressing them as multiples of the same power of 10.
It is important students understand that “multiple of a power of 10” does not mean integer multiple, necessarily. Tell students that they will be asked to express numbers as “multiples of a power of 10,” which might mean writing 52,000 as \((5.2) \boldcdot 10^4\), for example.
Here are some questions for discussion:
- “What are some ways you came up with to write 230,000,000 using powers of 10?” (Since the value of 230,000,000 will stay the same if it is multiplied by 10 and then divided by 10, we can think of it as: \(230,\!000,\!000 = 23,\!000,\!000 \boldcdot 10 = 2,\!300,\!000 \boldcdot 10^2 = \ldots = 23 \boldcdot 10^7 = (2.3) \boldcdot 10^8\).)
- “What are some of the ways you came up with to find the value of \((5.4) \boldcdot 10^5\)?” (The value of \((5.4) \boldcdot 10^5\) is 540,000 because \((5.4) \boldcdot 10^5 = 54 \boldcdot 10^4 = 540 \boldcdot 10^3 = \ldots = 540,\!000\).)
- “How did you compare which was faster—the speed of light through diamond and the speed of light through ice?” (The speed of light through diamond was given as \(124 \boldcdot 10^6\) meters per second, and the speed of light through ice was given as \((2.3) \boldcdot 10^8\) meters per second. The speed through diamond could be rewritten as \((1.24) \boldcdot 10^8\) meters per second, which makes it clear that it is slower than the speed of light through ice because \(1.24 < 2.3\).)
10.4: Cool-down - Describe the Point (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
There are many ways to compare two quantities. Suppose we want to compare the world population, about 7.4 billion
to the number of pennies the U.S. made in 2015, about
8,900,000,000
There are many ways to do this. We could write 7.4 billion as a decimal, 7,400,000,000, and then we can tell that there were more pennies made in 2015 than there are people in the world! Or we could use powers of 10 to write these numbers: \(\displaystyle 7.4 \boldcdot 10^9\) for people in the world and \(\displaystyle 8.9 \boldcdot 10^9\) for the number of pennies.
For a visual representation, we could plot these two numbers on a number line. We need to carefully choose our end points to make sure that the numbers can both be plotted. Since they both lie between \(10^9\) and \(10^{10}\), if we make a number line with tick marks that increase by one billion, or \(10^9\), we start the number line with 0 and end it with \(10 \boldcdot 10^{9}\), or \(10^{10}\). Here is a number line with the number of pennies and world population plotted: