Lesson 3
Representing Proportional Relationships
Lesson Narrative
Now that students have considered the scale from several perspectives, in this lesson they label and choose a scale for empty pairs of axes as part of graphing proportional relationships. In the first activity, students create representations of proportional relationships when given two to start from. For each representation, they identify key features such as the constant of proportionality and relate how they know that each representation is for the same situation. In the second activity, students use the info gap structure. The student with the problem card needs to graph a proportional relationship on an empty pair of axes that includes a specific point. In order to do so, they need to request information about the proportional relationship as well as calculate the specific point. The focus here is on the graphs students create and their decisions on how to scale the axes in an appropriate manner for the situation.
Learning Goals
Teacher Facing
- Create an equation and a graph to represent proportional relationships, including an appropriate scale and axes.
- Determine what information is needed to create graphs that represent proportional relationships. Ask questions to elicit that information.
Student Facing
Let's graph proportional relationships.
Required Materials
Required Preparation
Print and cut up cards from the Info Gap: Proportional Relationships blackline master. Prepare 1 set of cards for every 2 students. Provide all students with access to straightedges and graph paper.
Learning Targets
Student Facing
- I can scale and label coordinate axes in order to graph a proportional relationship.
Glossary Entries
-
rate of change
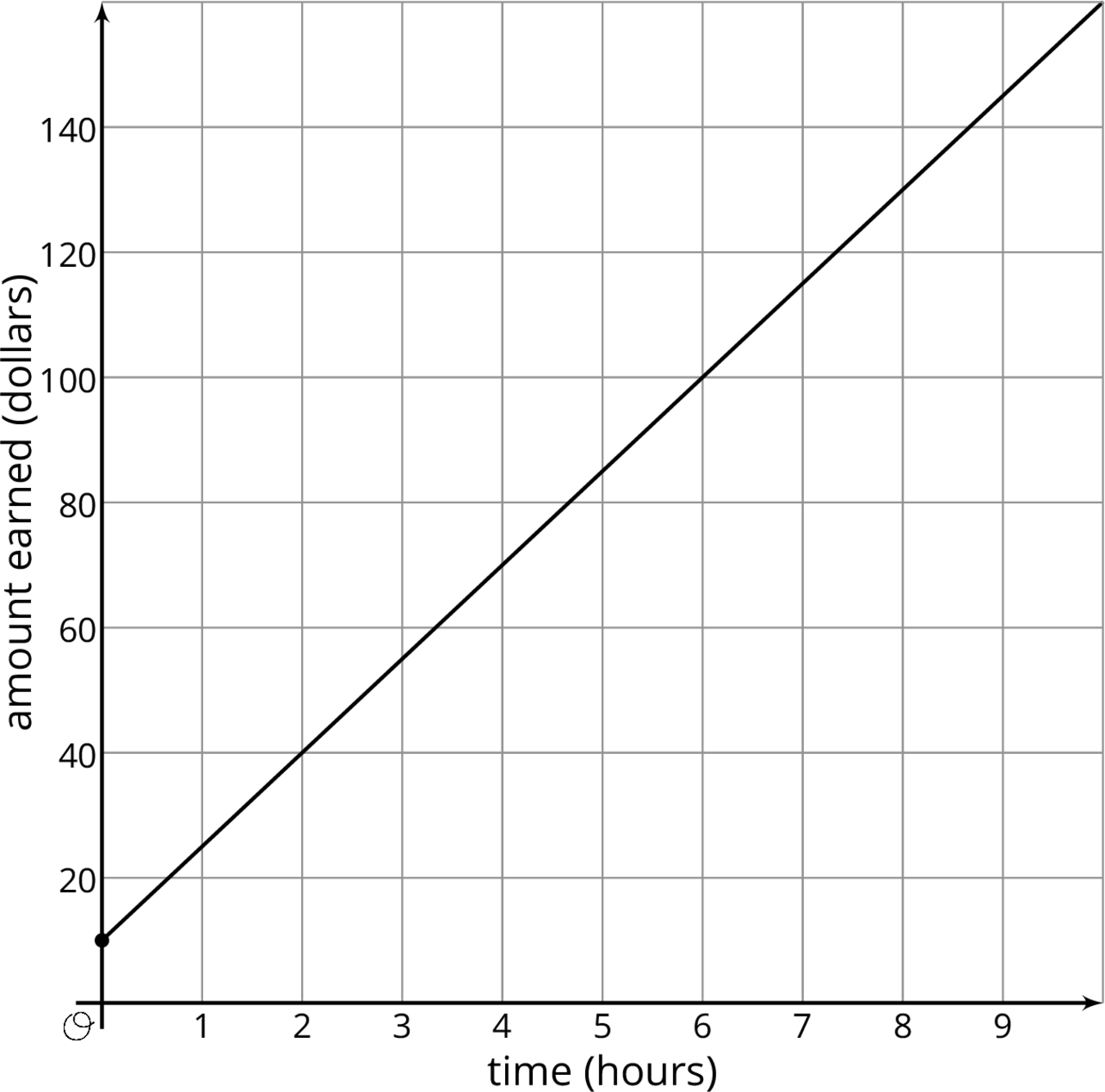
The rate of change in a linear relationship is the amount \(y\) changes when \(x\) increases by 1. The rate of change in a linear relationship is also the slope of its graph.
In this graph, \(y\) increases by 15 dollars when \(x\) increases by 1 hour. The rate of change is 15 dollars per hour.
Print Formatted Materials
For access, consult one of our IM Certified Partners.
Additional Resources
| Google Slides | For access, consult one of our IM Certified Partners. |
|
| PowerPoint Slides | For access, consult one of our IM Certified Partners. |