Lesson 5
Introduction to Linear Relationships
5.1: Number Talk: Fraction Division (5 minutes)
Warm-up
This number talk encourages students to think about the numbers in a computation problem and rely on what they know about structure, patterns, fractions, and division to mentally solve a problem. Only one problem is presented to allow students to share a variety of strategies for division. Encourage the students who solve the problem procedurally to think about the meaning of division and how that supports what they did.
Launch
Display the problem for all to see. Give students 2 minutes of quiet think time and ask them to give a signal when they have an answer and a strategy. Follow with a whole-class discussion.
Supports accessibility for: Memory; Organization
Student Facing
Find the value of \(2\frac58 \div \frac12\).
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Invite students to share their strategies. Record and display student explanations for all to see. Ask students to explain how they thought about the division problem and, if solved procedurally, why that strategy works. To involve more students in the conversation, consider asking:
- “Who can restate ___’s reasoning in a different way?”
- “Did anyone solve the problem the same way but would explain it differently?”
- “Did anyone solve the problem in a different way?”
- “Does anyone want to add on to _____’s strategy?”
- “Do you agree or disagree? Why?” At the end of the discussion, if time permits, ask a few students to share a story problem for which the expression \(2\frac58 \div \frac12\) represents the answer.
Design Principle(s): Optimize output (for explanation)
5.2: Stacking Cups (10 minutes)
Activity
In this task, students are presented with a situation that leads to a linear relationship that is not proportional because there is a non-zero starting amount. By trying to answer the question, “How many cups are needed to get to a height of 50 cm?” the students explore the rate of change, which is the increase per cup after the first cup. The rate of change can be seen in the graph as the slope. Students use representations and ideas from previous lessons on proportional relationships. They use tables and graphs to represent the situation and make deductions by generalizing from repeated reasoning (MP8), arguing that each additional cup increases the height of the stack by the same amount. As students are working, suggest that students make a graph or a table if they are stuck or if they have trouble explaining their reasoning. Students should be prepared to share their strategies with the class.
Students can attack this problem using any method. If they get stuck, here are some things it would be useful to figure out:
- How much height does each cup add?
- Is the first cup different from the others?
- Create a graph or table to help you reason about this problem.
As students work, identify students who use different strategies, i.e. graphs, tables, equations.
This activity and the next were written using a particular type of cup. Photos are included of all measurements needed, so these activities can be used without any additional preparation. However, if desired, the lesson could be modified so that students are measuring stacks of actual cups. The numbers then may have to be adjusted since the cups come in different sizes. Teachers who want to use real cups should measure the height of two stacks ahead of time, find the rate of change and make sure that it is approximately constant. Note that rounding error will likely play a role unless the number of cups in the stacks is chosen carefully, so some flexibility in answers may be necessary if students measure actual stacks of cups.
Launch
Before students look at the picture with all of the given information, display just this part of the picture.

Ask students how many cups they see, and how tall the stack is. (There are 6 cups, and the stack is 15 cm tall.) Then, ask students to quietly make a prediction about the height of 12 cups and give you a silent signal when they have a response. When everyone has come up with an answer, ask a few students to share their responses and write these on the board. It is likely that some students will say 30 centimeters, and some might have an argument for why the height of 12 cups must be less than 30 centimeters. This question will be resolved as soon as students look at the photo in the task. Tell students that their job is to figure out how many cups would be needed in order to stack them to a height of 50 centimeters.
Arrange students in groups of 2–4. Give access to rulers and graph paper. Allow individual think time of 3 minutes before students work together in groups.
Supports accessibility for: Conceptual processing; Memory
Design Principle(s): Optimize output (for explanation); Maximize meta-awareness
Student Facing
We have two stacks of styrofoam cups.
- One stack has 6 cups, and its height is 15 cm.
- The other stack has 12 cups, and its height is 23 cm.
How many cups are needed for a stack with a height of 50 cm?

Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students compute \(\frac{15}{6}=2.5\) or \(\frac{23}{12}=1.9\) and use this as the increase per cup. Measurement is approximate; students may be looking for exact, nice numbers. Make sure numbers agree approximately between students, but reassure them that they are close enough.
Activity Synthesis
Poll the class about the number of cups they came up with to reach a total height of 50 cm.
If the class used real cups, stack enough of them to get to a height of 50 cm, and let students check if they were correct. Otherwise display this photo:

Ask students who used different strategies to share their reasoning with the class.
Ask students if they think the relationship is proportional. If there is a disagreement, ask one person per opinion to share their reasons. Encourage them to come to the conclusion that it is not proportional since doubling the number of cups from 6 to 12 did not double the height. Students can see that when stacking the cups only the rim adds to the height. The first cup adds more height since there are additionally 7 cm from the bottom of the cup to the bottom of the rim.
Tell students that even though the relationship is not proportional, this relationship has things in common with proportional relationships, and that they will explore this in the next activity.
5.3: Connecting Slope to Rate of Change (15 minutes)
Activity
The previous task asks students to estimate how many cups it will take to create a 50 cm stack. Students observe that the height of the stack grows regularly with the number of cups, but it is not a proportional relationship. In this task, they examine the relationship more closely, graph the relationship, and then interpret the graph.
Each successive cup, after the first, adds the same amount of height to the stack. This amount of height added per cup is the rate of change for the relationship between number of cups in a stack and height of the stack. It is also the slope of the line that represents this relationship. This makes sense because the slope of a line can be calculated by finding the amount of change in \(y\) (the height of the stack) when \(x\) (the number of cups in the stack) increases by 1.
Students also find where their graph intersects the \(y\)-axis and interpret this value in terms of the situation: it is the height of the bottom part of the first cup, below the rim (MP2). If this part of the cups was removed, then the graph would go through \((0,0)\), and the relationship would be proportional because the stacks would just be stacks of the cup rims.
Monitor for students who recall work with slope triangles from the previous unit when they evaluate the slope of the line. A natural choice for a slope triangle in this case would be one with a horizontal side length that is a multiple of 3 and a vertical side length that is a multiple of 4 (the given data points would encourage a choice where the horizontal side length is 6 and the vertical side length is 8). As they interpret the meaning of the slope in the context, monitor for ration language, i.e. “the height added to the stack, in cm, per cup.”
Launch
Keep students in the same groups. Remind students that the number of cups and the height of the stack is not a proportional relationship. Ask students how they determined the number of cups needed to make a stack 50 cm in height. A table is a likely choice and the table had some nice structure, structure which allowed them to effectively make calculations and predictions, even though it was not a ratio table. Tell them that in this task, they are to examine that structure more carefully using a graph.
Give students 8–10 minutes of group work time and follow with a whole-class discussion.
Student Facing
-
If you didn’t create your own graph of the situation before, do so now.
- What are some ways you can tell that the number of cups is not proportional to the height of the stack?
- What is the slope of the line in your graph? What does the slope mean in this situation?
- At what point does your line intersect the vertical axis? What do the coordinates of this point tell you about the cups?
- How much height does each cup after the first add to the stack?
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may need a reminder of the meaning of slope for a line. Encourage them to begin by drawing a slope triangle.
Students may struggle with the question about the meaning of the \(y\)-intercept for the graph. Ask them to think about the cups. Ask them how much height is added with each cup after the first? What happens if you subtract this amount from the first cup?
Activity Synthesis
Begin by displaying a correct graph to support the discussion. Select students to use the graph and share:
- how they can tell the number of cups is not proportional to the height of the stack.
- how they calculated the slope of the line (on the grid, draw in any triangles used).
- what the point on the graph \((0,7)\) means. (It tells us the distance from the bottom to the rim of the first cup.)
Display the prompts “How can you see on the graph the amount that one cup adds to the height?” and give students 2–3 minutes of quiet work time to write a brief response. Select 3–4 students to share their responses. If not suggested by students, draw a slope triangle with a horizontal distance of 1 on the graph or display this image:

Draw a right triangle to see that each cup increases the height by \(\frac43\) cm.
It is important to bring out here that the rate per 1, \(\frac43\), is not the constant of proportionality, since this is not a proportional relationship! This value is how much each cup adds to the height of the stack, and it is called the “rate of change.” The rate of change of \(y\) in a linear relationship between \(x\) and \(y\) is the increase in \(y\) when \(x\) increases by 1. Note that the rate of change of the relationship has the same value as the slope of the line representing the relationship. So asking “what is the slope?” is the same as asking “how much height does each cup after the first add to the stack?”
Lastly, students’ graphs may consist either of discrete points corresponding to coordinate pairs (number of cups, height) or of the entire line as shown in the solution. It is understood that only the points that represent a whole number of cups have a valid interpretation in the context. This continuous graphical representation of a linear relationship, whether the context is continuous or discrete, is very common and will be seen throughout this unit.
Design Principle(s): Support sense-making
Lesson Synthesis
Lesson Synthesis
The main focus of this lesson is the transition from proportional relationships to linear relationships that are not proportional:
- Understand that there are linear relationships that are not proportional.
- Note that the rate of change of the linear relationship is the same value as the slope of a line representing the relationship.
- Interpret the rate of change in the context of the situation.
In order to highlight this focus, ask students:
- “How can we tell if a linear relationship is proportional or not? From the graph? From a table? From the context?” (Check that when both variables are 0, this makes sense: on the graph, in the table, or in the context.)
- “What does the rate of change of a linear relationship tell us?” (The slope of the graph.)
5.4: Cool-down - Stacking More Cups (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
Andre starts babysitting and charges \$10 for traveling to and from the job, and \$15 per hour. For every additional hour he works he charges another \$15. If we graph Andre's earnings based on how long he works, we have a line that starts at \$10 on the vertical axis and then increases by \$15 each hour. A linear relationship is any relationship between two quantities where one quantity has a constant rate of change with respect to the other.
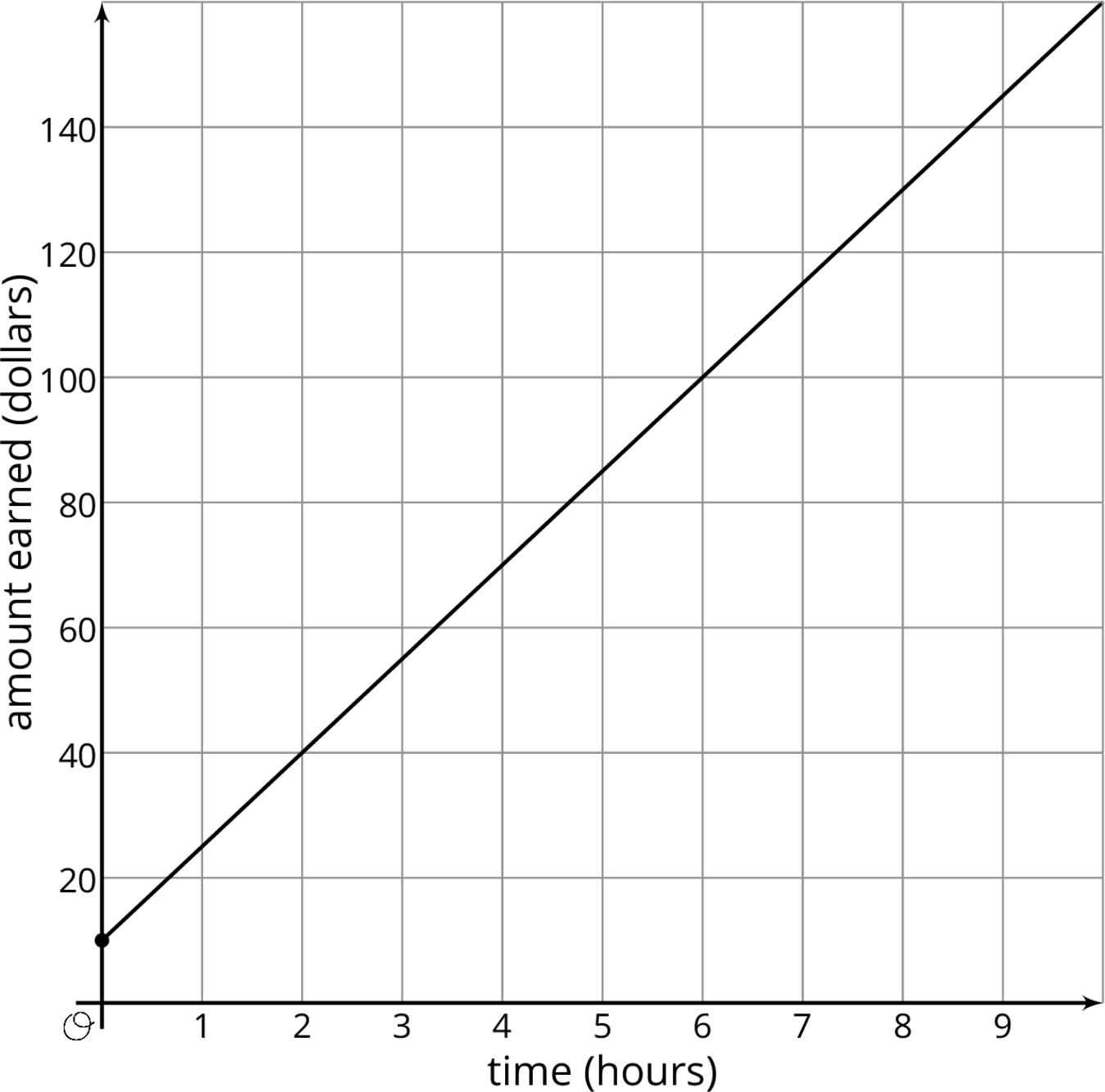
We can figure out the rate of change using the graph. Because the rate of change is constant, we can take any two points on the graph and divide the amount of vertical change by the amount of horizontal change. For example, take the points \((2, 40)\) and \((6, 100)\). They mean that Andre earns \$40 for working 2 hours and \$100 for working 6 hours. The rate of change is \(\frac{100-40}{6-2} = 15\) dollars per hour. Andre's earnings go up \$15 for each hour of babysitting.
Notice that this is the same way we calculate the slope of the line. That's why the graph is a line, and why we call this a linear relationship. The rate of change of a linear relationship is the same as the slope of its graph.
With proportional relationships we are used to graphs that contain the point \((0,0)\). But proportional relationships are just one type of linear relationship. In the following lessons, we will continue to explore the other type of linear relationship where the quantities are not both 0 at the same time.