Lesson 8
Translating to $y=mx+b$
8.1: Lines that Are Translations (5 minutes)
Warm-up
The purpose of this warm-up is to remind students that the translation of a line is parallel to the original line, and to plant the seed that a line can be taken to a parallel line by translating it. They inspect several lines to decide which could be translations of a given line. Then they describe the translations by specifying the number of units and the direction the original line should be translated.
Launch
Arrange students in groups of 2. Give students 2 minutes of quiet think time and access to geometry toolkits. Ask them to share their responses with a partner afterwards.
Student Facing
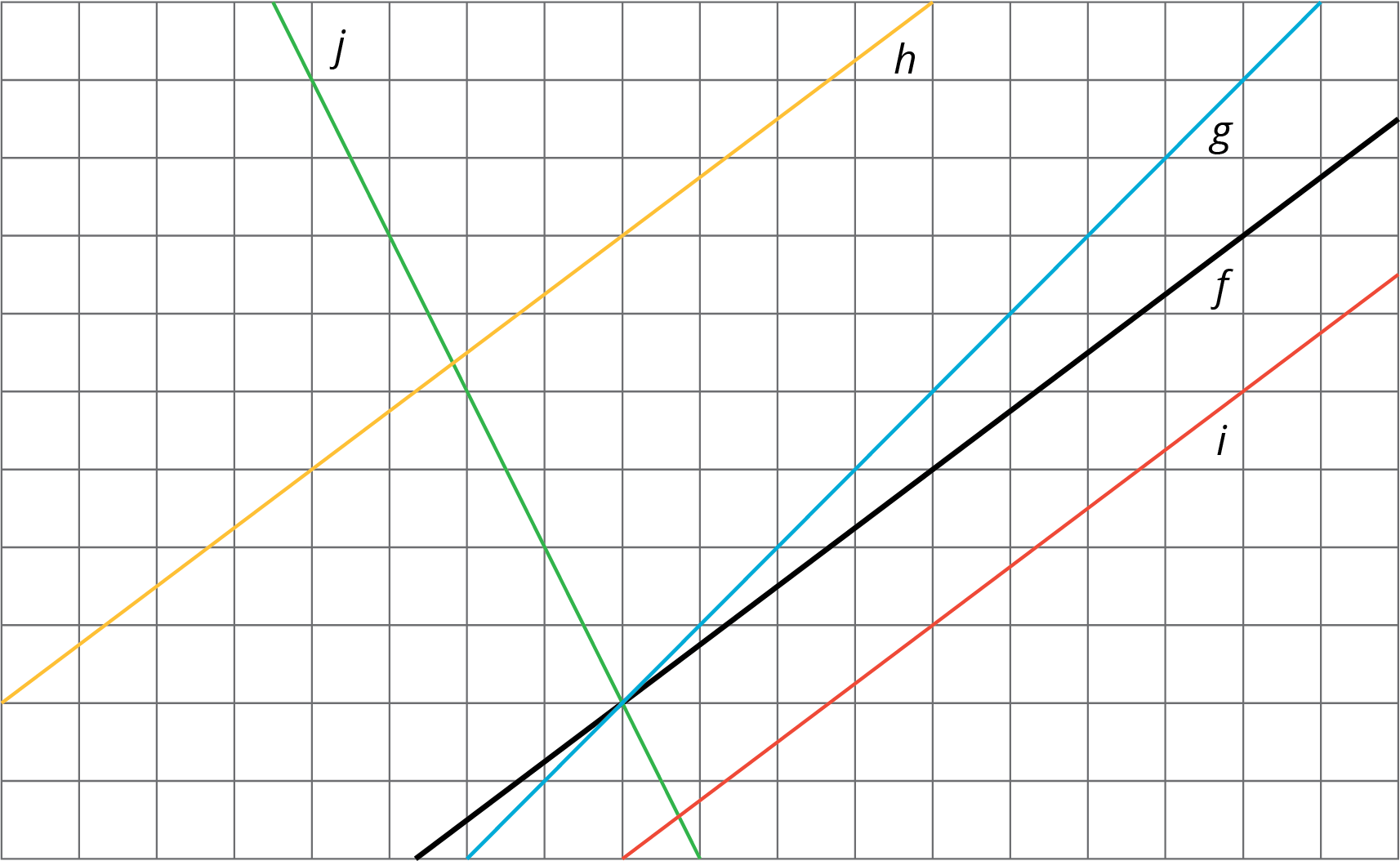
The diagram shows several lines. You can only see part of the lines, but they actually continue forever in both directions.
- Which lines are images of line \(f\) under a translation?
- For each line that is a translation of \(f\), draw an arrow on the grid that shows the vertical translation distance.
Student Response
For access, consult one of our IM Certified Partners.
Anticipated Misconceptions
Students may think that lines \(i\) and \(h\) can’t be images of line \(f\) because the part of \(i\) and \(h\) we can see is shorter than the part of \(f\) we can see. Tell these students that all of the lines go on indefinitely in both directions.
Activity Synthesis
Invite students to share how they know that lines \(h\) and \(i\) are translations of \(f\). The main reason to bring out is that they are parallel to \(f\). It might be worth demonstrating with a transparency that we can translate \(f\) to match up with \(h\) and \(i\), but to match up with the other lines, we would need to rotate (or reflect) the transparency. If using a transparency to demonstrate the number of units to translate \(f\) up or down, it is helpful to draw a dot on a specific point on both the underlying graph and on the transparency.
8.2: Increased Savings (15 minutes)
Activity
The goal of this activity is to get students to think about translations of lines in a context. Students examine two scenarios. In the first, there is a proportional relationship between the number of hours Diego works and his total earnings. In the second, Diego starts with $30 saved and then saves all of his earnings. Graphically, the two lines showing these relationships are parallel (the second is a vertical translation of the first for the extra $30 Diego has already saved). The lines have the same slope (Diego’s hourly rate of pay is the same) but different \(y\)-intercepts (one has a \(y\)-intercept of 0 while the other has a \(y\)-intercept of 30). Students will observe this structure in the equations that they write for the two lines.
Even though babysitters are most often paid for increments of 1 hour or \(\frac12\) hour and in increments of $1, this uses a continuous line to represent this relationship. If a student brings up the idea that it would be better to represent the relationship using discrete points than a line, acknowledge the observation but suggest that a continuous line is an acceptable representation. Mathematically proficient students who can apply what they know are comfortable making assumptions and approximations to simplify a complicated situation (MP4).
Monitor for students who use these approaches as they graph the two earnings scenarios:
- Making a table (showing earnings for different numbers of hours worked) and then graphing
- Plotting points directly
- Writing an equation that represents the situation and then graphing the solutions to the equation
Select students using these approaches and invite them to present during the discussion.
Launch
Give students 5 minutes of quiet work time and tell them to pause after the first 3 questions. After they have discussed their responses with a partner, ensure that students have graphed both situations correctly and can articulate that the second graph can be viewed as a vertical translation of the first graph. Then, instruct students to complete the remaining question either independently or with a partner.
If using the digital activity, the mathematical thinking and reasoning remains the same. The applet, however, will assist students in creating graphs to model the babysitting scenarios. Furthermore, some students may start exploring translations in general by creating multiple rays. The structure for the lesson will remain the same for print and digital.
Supports accessibility for: Language; Social-emotional skills
Student Facing
-
Diego earns $10 per hour babysitting. Assume that he has no money saved before he starts babysitting and plans to save all of his earnings. Graph how much money, \(y\), he has after \(x\) hours of babysitting.
-
Now imagine that Diego started with $30 saved before he starts babysitting. On the same set of axes, graph how much money, \(y\), he would have after \(x\) hours of babysitting.
-
Compare the second line with the first line. How much more money does Diego have after 1 hour of babysitting? 2 hours? 5 hours? \(x\) hours?
-
Write an equation for each line.
Student Response
For access, consult one of our IM Certified Partners.
Launch
Give students 5 minutes of quiet work time and tell them to pause after the first 3 questions. After they have discussed their responses with a partner, ensure that students have graphed both situations correctly and can articulate that the second graph can be viewed as a vertical translation of the first graph. Then, instruct students to complete the remaining question either independently or with a partner.
If using the digital activity, the mathematical thinking and reasoning remains the same. The applet, however, will assist students in creating graphs to model the babysitting scenarios. Furthermore, some students may start exploring translations in general by creating multiple rays. The structure for the lesson will remain the same for print and digital.
Supports accessibility for: Language; Social-emotional skills
Student Facing
-
Diego earns $10 per hour babysitting. Assume that he has no money saved before he starts babysitting and plans to save all of his earnings. Graph how much money, \(y\), he has after \(x\) hours of babysitting.
-
Now imagine that Diego started with $30 saved before he starts babysitting. On the same set of axes, graph how much money, \(y\), he would have after \(x\) hours of babysitting.
-
Compare the second line with the first line. How much more money does Diego have after 1 hour of babysitting? 2 hours? 5 hours? \(x\) hours?
-
Write an equation for each line.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Invite selected students to share their methods for graphing Diego’s earnings, sequenced in this order:
- Making a table (showing earnings for different numbers of hours worked) and then graphing
- Plotting points directly
- Writing an equation that represents the situation and then graphing the solutions to the equation
Notice that making a table has the advantage of revealing the arithmetic relationship between Diego’s earnings in the two situations. No matter how many hours, Diego works, he has $30 more in the second situation. Plotting the points directly shows geometrically that the vertical distance is always the same between pairs of points for the same number of hours worked (this vertical distance represents the $30). The equations are the most abstract and contain all of the arithmetic and geometric information once we can interpret them. If \(h\) is the number of hours Diego works and \(m\) is how much money he has saved, then the two equations can be written as \(m = 10h\) and \(m = 30 + 10h\). The graphs of these lines have slope 10 (and they are parallel!), but the second equation has a \(y\)-intercept of 30 while the first has a \(y\)-intercept of 0. The graph of \(m = 30+10h\) is the same as the graph of \(m = 10h\) except that every point is moved up by the same amount (this explains why they are parallel).
Have students connect the equations and situations they have graphed in the activity by asking students what the graph of \(m = 20 + 10h\) would look like (it would lie between the graphs of \(m = 30 + 10h\) and \(m = 10h\)). What situation does this equation represent? (Diego started with $20 saved and then earned $10 for each hour of baby sitting.)
Design Principle(s): Optimize output (for comparison); Cultivate conversation
8.3: Translating a Line (15 minutes)
Activity
The previous activity examined parallel lines and equations that define them, focusing on their common attributes (slope) and their different attributes (\(y\)-intercept). This activity further examines parallel lines, including situations where the \(y\)-intercept is negative. In addition, students match lines represented in many different ways including
- graphically
- verbal description
- table of values
- equations
You will need the Translating a Line blackline master for this activity.
Launch
Arrange students in groups of 2. Students first identify equations that describe a line with a negative \(y\)-intercept, then they complete a matching activity involving graphs, equations, and tables.
Display the image in the activity. Ask students how the pair of lines is the same and different from the lines in the previous activity. Instead of being translated up, line \(a\) was translated down. Ask students to explain how to change \(y=\frac14x\), an equation representing line \(a\), to represent line \(h\). They should readily come up with \(y=\frac14 x-5\). Ask students for another way to write the same equation, for example, \(\frac14 x - 5 = y\). The first part of the activity is about finding different ways to write this equation.
Tell students to complete the first part of the activity and then pause for discussion. Ensure that all understand why the incorrect equations are incorrect, then distribute the cards to sort. Tell students to take turns identifying cards that go together, and for each choice they make, explain to their partner why they think they go together. Once they have sorted them into groups, they write an equation on the blank card to represent the line that does not have an equation.
Supports accessibility for: Visual-spatial processing
Student Facing
- Experiment with moving point \(A\).
- Place point \(A\) in three different locations above the \(x\)-axis. For each location, write the equation of the line and the coordinates of point \(A\).
- Place point \(A\) in three different locations below the \(x\)-axis. For each location, write the equation of the line and the coordinates of point \(A\).
- In the equations, what changes as you move the line? What stays the same?
- If the line passes through the origin, what equation is displayed? Why do you think this is the case?
- Your teacher will give you 12 cards. There are 4 pairs of lines, A–D, showing the graph, \(a\), of a proportional relationship and the image, \(h\), of \(a\) under a translation. Match each line \(h\) with an equation and either a table or description. For the line with no matching equation, write one on the blank card.
Student Response
For access, consult one of our IM Certified Partners.
Launch
Arrange students in groups of 2. Students first identify equations that describe a line with a negative \(y\)-intercept, then they complete a matching activity involving graphs, equations, and tables.
Display the image in the activity. Ask students how the pair of lines is the same and different from the lines in the previous activity. Instead of being translated up, line \(a\) was translated down. Ask students to explain how to change \(y=\frac14x\), an equation representing line \(a\), to represent line \(h\). They should readily come up with \(y=\frac14 x-5\). Ask students for another way to write the same equation, for example, \(\frac14 x - 5 = y\). The first part of the activity is about finding different ways to write this equation.
Tell students to complete the first part of the activity and then pause for discussion. Ensure that all understand why the incorrect equations are incorrect, then distribute the cards to sort. Tell students to take turns identifying cards that go together, and for each choice they make, explain to their partner why they think they go together. Once they have sorted them into groups, they write an equation on the blank card to represent the line that does not have an equation.
Supports accessibility for: Visual-spatial processing
Student Facing
This graph shows two lines.
Line \(a\) goes through the origin \((0, 0)\).
Line \(h\) is the image of line \(a\) under a translation.

-
Select all of the equations whose graph is line \(h\).
- \(y = \frac14 x - 5\)
- \(y = \frac14x + 5\)
- \(\frac14x - 5 = y\)
-
\(y = \text-5 + \frac14x\)
-
\(\text-5 + \frac14x = y\)
-
\(y = 5 - \frac14x\)
- Your teacher will give you 12 cards. There are 4 pairs of lines, A–D, showing the graph, \(a\), of a proportional relationship and the image, \(h\), of \(a\) under a translation. Match each line \(h\) with an equation and either a table or description. For the line with no matching equation, write one on the blank card.
Student Response
For access, consult one of our IM Certified Partners.
Student Facing
Are you ready for more?
A student says that the graph of the equation \(y = 3(x+8)\) is the same as the graph of \(y = 3x\), only translated upwards by 8 units. Do you agree? Why or why not?
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
Once all groups have completed the matching, discuss the following:
- “Were any of the matches more difficult than others? What made them difficult?”
- “Did any groups have to adjust an initial guess that turned out to be wrong? What adjustments were made and why?”
- “What clues did you look for to see which equation went with a graph?”
Solicit all versions of the missing equation. Ensure that students understand that \(y=\frac12x-4\) and \(y=\text -4+\frac12x\) are equivalent.
Design Principle(s): Support sense-making, Optimize output (for explanation)
Lesson Synthesis
Lesson Synthesis
Display a graph of two lines on the same set of axes: one of the form \(y=mx\) and the other of the form \(y=mx+b\). Discuss:
- “How can we think of one of these lines as a transformation of the other?”
- “What is the equation of the line that goes through the origin?” (Discuss how you need to figure out the slope.)
- “How is the equation of the line that does not go through the origin different?” (Make sure to bring out that the \(b\) in \(mx + b\) gives the vertical translation to get from the graph of \(y = mx\) to the graph of \(y = mx + b\); the translation is up when \(b > 0\) and down when \(b < 0\).)
8.4: Cool-down - Similarities and Differences in Two Lines (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.
Student Lesson Summary
Student Facing
During an early winter storm, the snow fell at a rate of \(\frac12\) inch per hour. We can see the rate of change, \(\frac12\), in both the equation that represents this storm, \(y=\frac12x\), and in the slope of the line representing this storm.
In addition to being a linear relationship between the time since the beginning of the storm and the depth of the snow, we can also call this as a proportional relationship since the depth of snow was 0 at the beginning of the storm.

During a mid-winter storm, the snow again fell at a rate of \(\frac12\) inch per hour, but this time there was already 5 inches of snow on the ground.

We can graph this storm on the same axes as the first storm by taking all the points on the graph of the first storm and translating them up 5 inches.
Two hours after each storm begins, 1 inch of new snow has fallen. For the first storm, this means there is now 1 inch of snow on the ground. For the second storm, this means there are now 6 inches of snow on the ground.
Unlike the first storm, the second is not a proportional relationship since the line representing the second storm has a vertical intercept of 5. The equation representing the storm, \(y=\frac12x+5\), is of the form \(y=mx+b\), where \(m\) is the rate of change, also the slope of the graph, and \(b\) is the initial amount, also the vertical intercept of the graph.