Lesson 2
Adjacent Angles
Let’s look at some special pairs of angles.
Problem 1
Angles \(A\) and \(C\) are supplementary. Find the measure of angle \(C\).
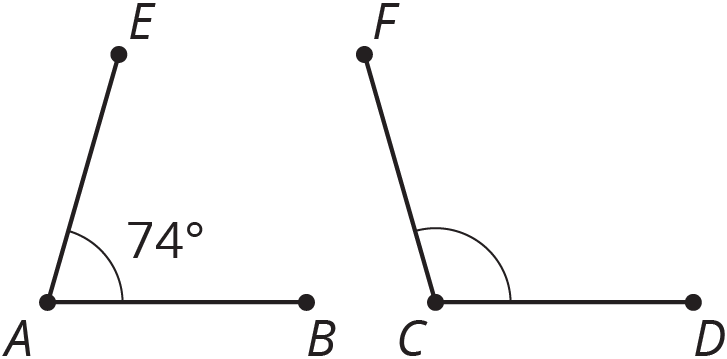
Problem 2
-
List two pairs of angles in square \(CDFG\) that are complementary.
- Name three angles that sum to \(180^\circ\).
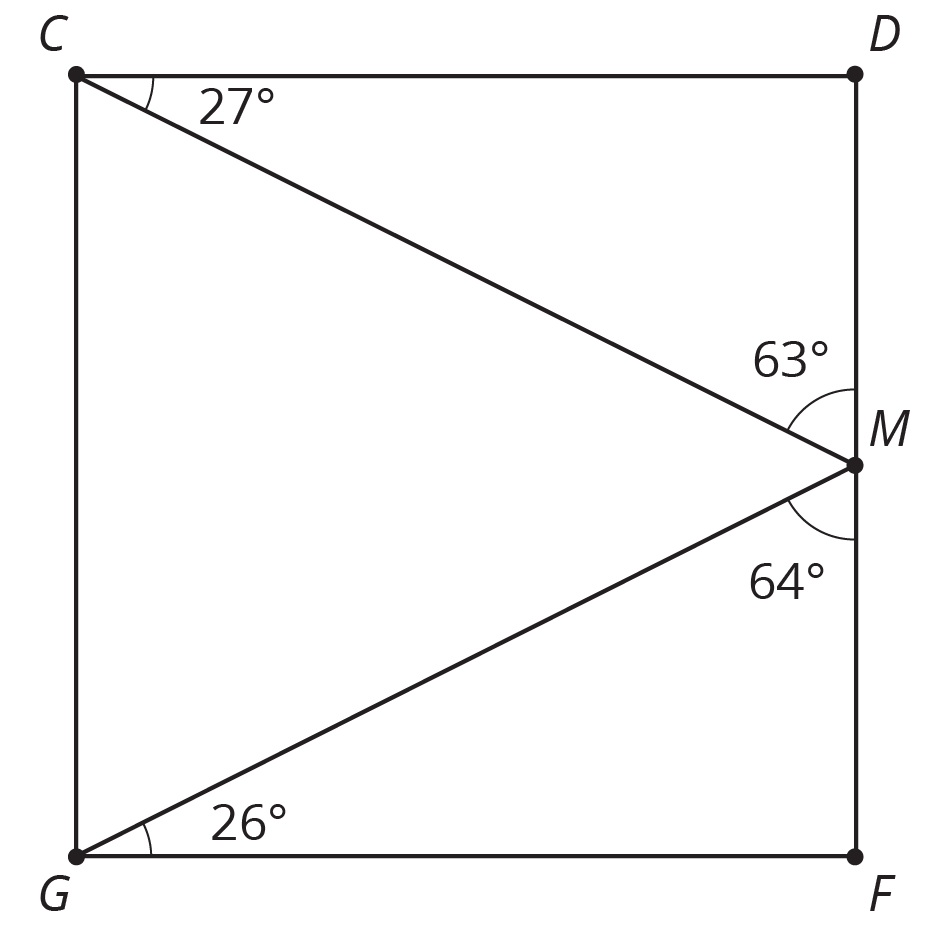
Problem 3
Complete the equation with a number that makes the expression on the right side of the equal sign equivalent to the expression on the left side.
\(\displaystyle 5x-2.5 +6x-3 = \underline{\ \ \ \ }(2x-1)\)
Problem 4
Match each table with the equation that represents the same proportional relationship.