Lesson 10

Drawing Triangles (Part 2)

Let’s draw some more triangles.

Problem 1

A triangle has sides of length 7 cm, 4 cm, and 5 cm. How many unique triangles can be drawn that fit that description? Explain or show your reasoning.

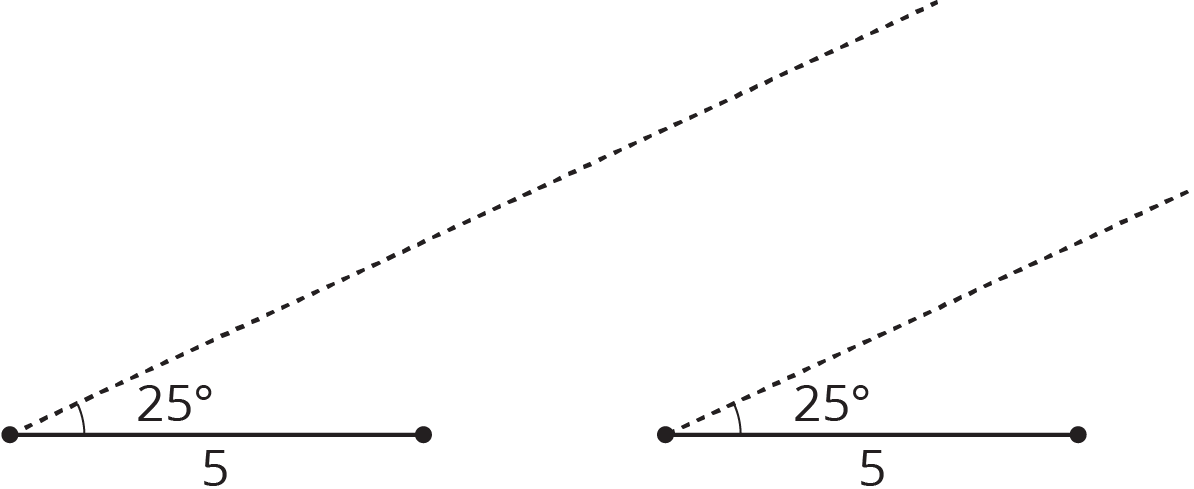
Problem 2

A triangle has one side that is 5 units long and an adjacent angle that measures \(25^\circ\). The two other angles in the triangle measure \(90^\circ\) and \(65^\circ\). Complete the two diagrams to create two different triangles with these measurements.

Two images, each a segment with side 5 and a dotted line rising at a 25 degree angle from the segment.

Problem 3

Is it possible to make a triangle that has angles measuring 90 degrees, 30 degrees, and 100 degrees? If so, draw an example. If not, explain your reasoning.

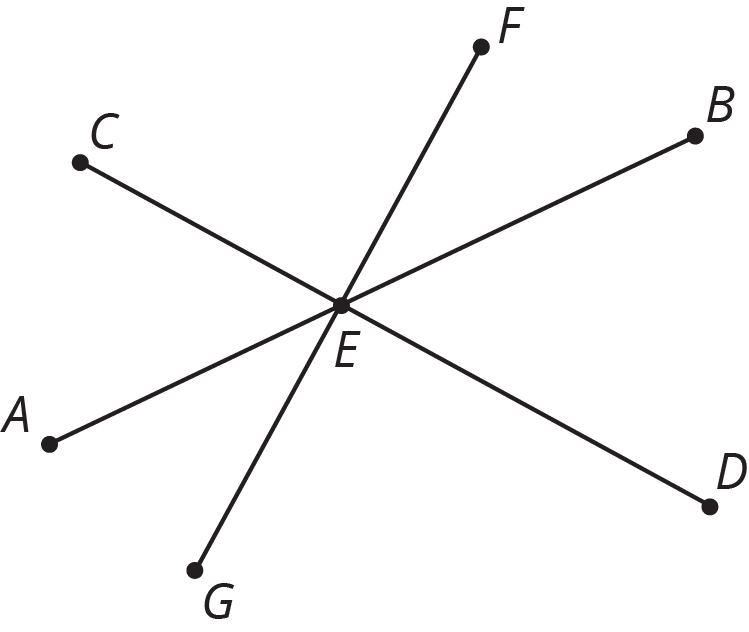
Problem 4

Segments \(CD\), \(AB\), and \(FG\) intersect at point \(E\). Angle \(FEC\) is a right angle. Identify any pairs of angles that are complementary.

Segment C D, segment A, B, segment F G intersect at point E. Clockwise, the points are C, F, B, D, G, A. Angle F E C is a right angle.
(From Unit 7, Lesson 2.)

Problem 5

Match each equation to a step that will help solve the equation for \(x\).

A:

\(3x=\text-4\)

B:

\(\text-4.5 = x-3\)

C:

\(3=\frac {\text{-}x}{3}\)

D:

\(\frac13=\text-3x\)

E:

\(x-\frac{1}{3}=0.4\)

F:

\(3+x=8\)

G:

\(\frac{x}{3}=15\)

H:

\(7=\frac{1}{3}+x\)

1:

Add \(\frac13\) to each side.

2:

Add \(\frac {\text{-}1}{3}\) to each side.

3:

Add \(3\) to each side.

4:

Add \(\text-3\) to each side.

5:

Multiply each side by 3..

6:

Multiply each side by \(\text-3\).

7:

Multiply each side by \(\frac13\).

8:

Multiply each side by \(\frac {\text{-}1}{3}\)

(From Unit 5, Lesson 15.)

Problem 6

  1. If you deposit $300 in an account with a 6% interest rate, how much will be in your account after 1 year?
  2. If you leave this money in the account, how much will be in your account after 2 years?
(From Unit 4, Lesson 8.)