Lesson 7

Reasoning about Solving Equations (Part 1)

Let’s see how a balanced hanger is like an equation and how moving its weights is like solving the equation.

Problem 1

There is a proportional relationship between the volume of a sample of helium in liters and the mass of that sample in grams. If the mass of a sample is 5 grams, its volume is 28 liters. \((5, 28)\) is shown on the graph below.

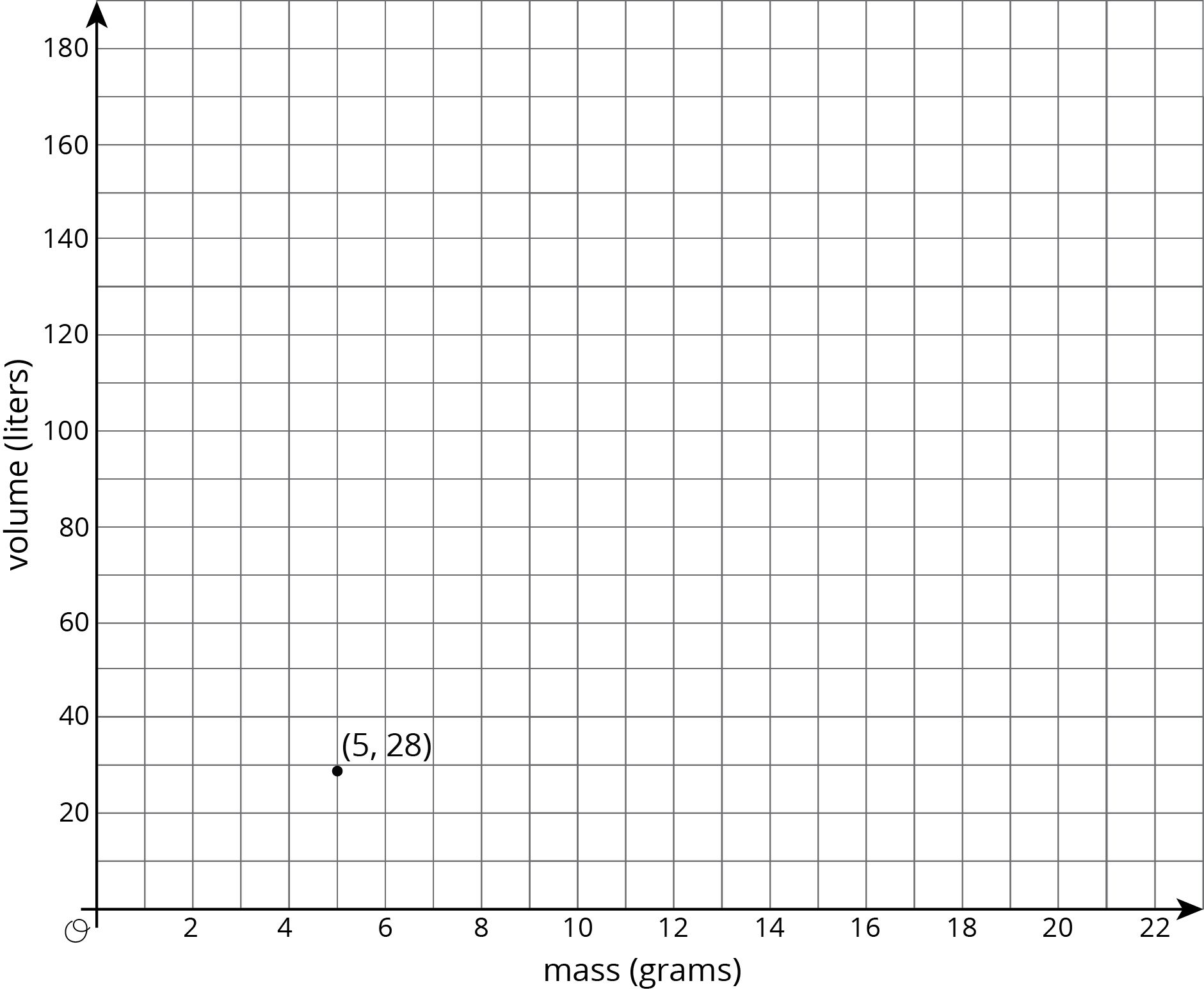
A coordinate plane, origin O labeled.  Horizontal axis, mass in grams, 0 to 22 by twos. Veritcal axis, volume in liters, 0 to 180 by twenties, a point labeled, 5 comma 28.
  1. What is the constant of proportionality in this relationship?
  2. In this situation, what is the meaning of the number you found in part a?
  3. Add at least three more points to the graph above, and label with their coordinates.
  4. Write an equation that shows the relationship between the mass of a sample of helium and its volume. Use \(m\) for mass and \(v\) for volume.
(From Unit 2, Lesson 11.)

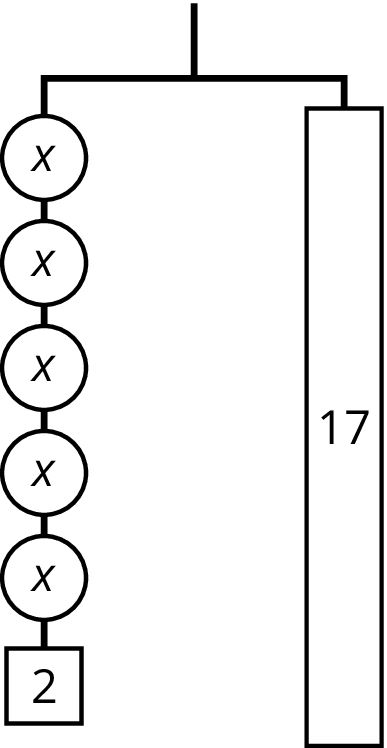
Problem 2

Explain how the parts of the balanced hanger compare to the parts of the equation.

\(7=2x+3\)

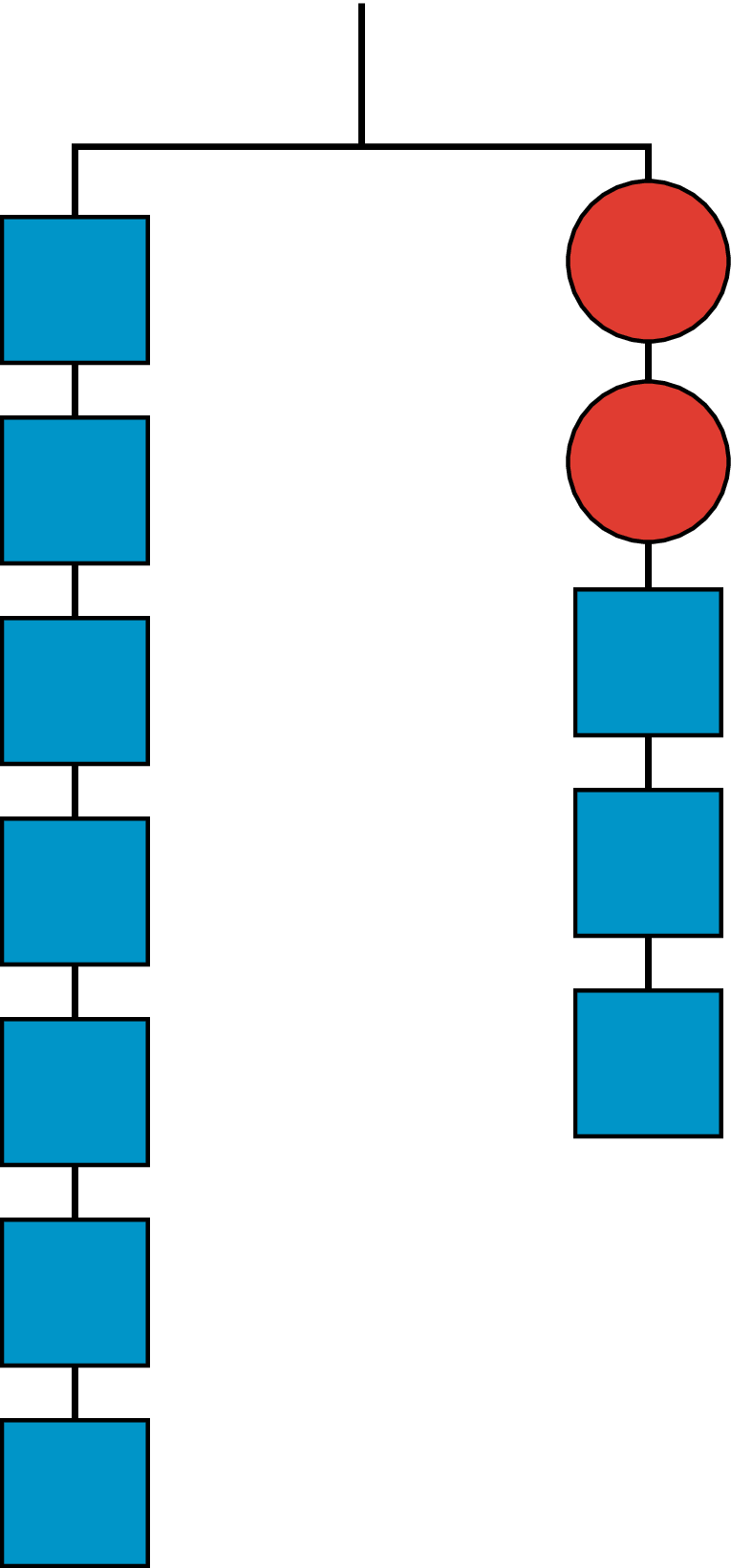
Balanced hanger, left side, 7 blue squares, right side, 2 red circles, 3 blue squares.

Problem 3

For the hanger below:

  1. Write an equation to represent the hanger.
  2. Draw more hangers to show each step you would take to find \(x\). Explain your reasoning.
  3. Write an equation to describe each hanger you drew. Describe how each equation matches its hanger.
Balanced hanger, left side, 5 circles labeled x, 1 square labeled 2, right side, rectangle labeled 17.