Lesson 5

Reasoning about Equations and Tape Diagrams (Part 2)

Let’s use tape diagrams to help answer questions about situations where the equation has parentheses.

Problem 1

Here are some prices customers paid for different items at a farmer’s market.  Find the cost for 1 pound of each item.

  1. $5 for 4 pounds of apples
  2. $3.50 for \(\frac12\) pound of cheese
  3. $8.25 for \(1\frac12\) pounds of coffee beans
  4. $6.75 for \(\frac34\) pounds of fudge
  5. $5.50 for a \(6\frac14\) pound pumpkin
(From Unit 4, Lesson 2.)

Problem 2

Find the products.

  1. \(\frac23 \boldcdot \left(\frac {\text{-}4}{5}\right)\)
  2. \(\left(\frac {\text{-}5}{7}\right) \boldcdot \left(\frac {\text7}{5}\right)\)
  3. \(\left(\frac {\text{-}2}{39}\right) \boldcdot 39\)
  4. \(\left(\frac {\text2}{5}\right) \boldcdot \left(\frac {\text{-}3}{4}\right)\)
(From Unit 5, Lesson 9.)

Problem 3

Here are two stories:

  • A family buys 6 tickets to a show. They also each spend $3 on a snack. They spend $24 on the show.
     
  • Diego has 24 ounces of juice. He pours equal amounts for each of his 3 friends, and then adds 6 more ounces for each.

Here are two equations:

  • \(3(x+6)=24\)
  • \(6(x+3)=24\)
  1. Which equation represents which story?
  2. What does \(x\) represent in each equation?
  3. Find the solution to each equation. Explain or show your reasoning.
  4. What does each solution tell you about its situation?

Problem 4

Here is a diagram and its corresponding equation. Find the solution to the equation and explain your reasoning.

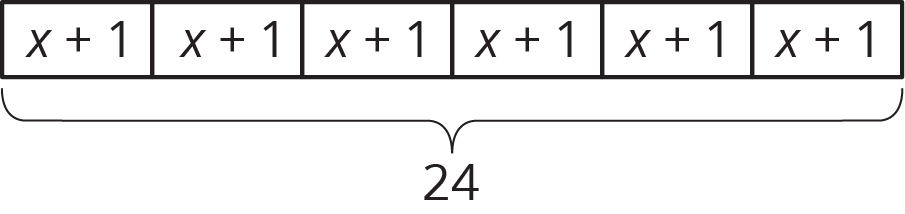
Tape diagram, 6 equal parts labeled x + 1, total 24

\(\displaystyle 6(x+1)=24\)

Problem 5

Below is a set of data about temperatures. The range of a set of data is the distance between the lowest and highest value in the set. What is the range of these temperatures?

\(9^\circ \text{C}, \text-3^\circ \text{C}, 22^\circ \text{C}, \text-5^\circ \text{C}, 11^\circ \text{C}, 15^\circ \text{C}\)

(From Unit 5, Lesson 7.)

Problem 6

A store is having a 25% off sale on all shirts. Show two different ways to calculate the sale price for a shirt that normally costs $24.

(From Unit 4, Lesson 11.)