Lesson 3

Reasoning about Equations with Tape Diagrams

Let’s see how equations can describe tape diagrams.

Problem 1

Solve each equation mentally.

  1. \(2x = 10\)
  2. \(\text-3x = 21\)
  3. \(\frac13 x = 6\)
  4. \(\text-\frac12x = \text-7\)
(From Unit 5, Lesson 15.)

Problem 2

Complete the magic squares so that the sum of each row, each column, and each diagonal in a grid are all equal.​

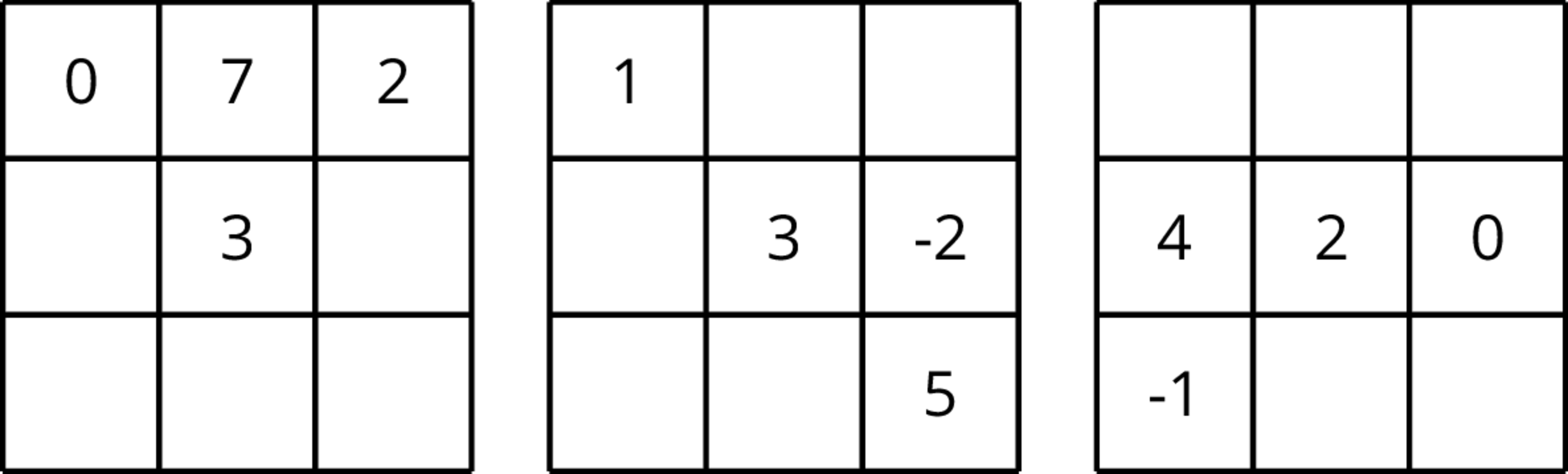
Three square grids.
(From Unit 5, Lesson 3.)

Problem 3

Draw a tape diagram to match each equation.

  1. \(5(x+1)=20\)

  2. \(5x+1=20\)

Problem 4

Select all the equations that match the tape diagram.

Tape diagram, 1 part labeled 8, 6 parts labeled x, total 35.
A:

\(35=8+x+x+x+x+x+x\)

B:

\(35=8+6x\)

C:

\(6+8x=35\)

D:

\(6x+8=35\)

E:

\(6x+8x=35x\)

F:

\(35-8=6x\)

Problem 5

Each car is traveling at a constant speed. Find the number of miles each car travels in 1 hour at the given rate.

  1. 135 miles in 3 hours

  2. 22 miles in \(\frac12\) hour

  3. 7.5 miles in \(\frac14\) hour

  4. \(\frac{100}{3}\) miles in \(\frac23\) hour

  5. \(97\frac12\) miles in \(\frac32\) hour

(From Unit 4, Lesson 2.)