Lesson 16
Interpreting Inequalities
Let’s write inequalities.
Problem 1
Priya looks at the inequality \(12-x>5\) and says “I subtract a number from 12 and want a result that is bigger than 5. That means that the solutions should be values of \(x\) that are smaller than something.”
Do you agree with Priya? Explain your reasoning and include solutions to the inequality in your explanation.
Problem 2
When a store had sold \(\frac25\) of the shirts that were on display, they brought out another 30 from the stockroom. The store likes to keep at least 150 shirts on display. The manager wrote the inequality \(\frac35x+30 \geq 150\) to describe the situation.
- Explain what \(\frac35\) means in the inequality.
-
Solve the inequality.
- Explain what the solution means in the situation.
Problem 3
You know \(x\) is a number less than 4. Select all the inequalities that must be true.
\(x<2\)
\(x+6<10\)
\(5x<20\)
\(x-2>2\)
\(x<8\)
Problem 4
Here is an unbalanced hanger.
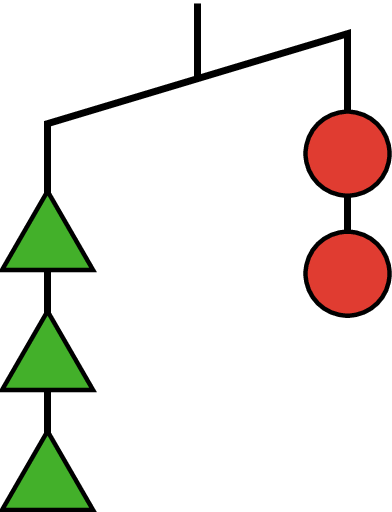
- If you knew each circle weighed 6 grams, what would that tell you about the weight of each triangle? Explain your reasoning.
- If you knew each triangle weighed 3 grams, what would that tell you about the weight of each circle? Explain your reasoning.
Problem 5
Match each sentence with the inequality that could represent the situation.
Problem 6
At a skateboard shop:
- The price tag on a shirt says $12.58. Sales tax is 7.5% of the price. How much will you pay for the shirt?
- The store buys a helmet for $19.00 and sells it for $31.50. What percentage was the markup?
- The shop pays workers $14.25 per hour plus 5.5% commission. If someone works 18 hours and sells $250 worth of merchandise, what is the total amount of their paycheck for this pay period? Explain or show your reasoning.