Lesson 14
Finding Solutions to Inequalities in Context
Let’s solve more complicated inequalities.
Problem 1
The solution to \(5-3x > 35\) is either \(x>\text-10\) or \(\text-10>x\). Which solution is correct? Explain how you know.
Problem 2
The school band director determined from past experience that if they charge \(t\) dollars for a ticket to the concert, they can expect attendance of \(1000-50t\). The director used this model to figure out that the ticket price needs to be $8 or greater in order for at least 600 to attend. Do you agree with this claim? Why or why not?
Problem 3
Which inequality is true when the value of \(x\) is -3?
\(\text-x -6 < \text-3.5\)
\(\text-x- 6 >3.5\)
\(\text-x -6 > \text-3.5\)
\(x -6 > \text-3.5\)
Problem 4
Draw the solution set for each of the following inequalities.
-
\(x\leq5\)
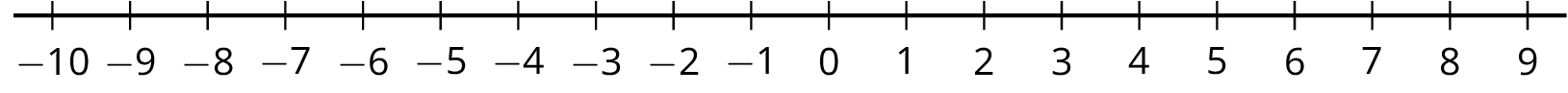
-
\(x<\frac52\)
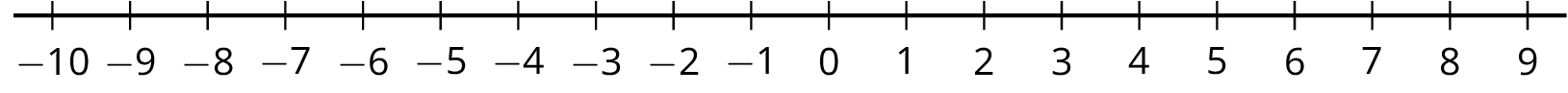
Problem 5
Write three different equations that match the tape diagram.

Problem 6
A baker wants to reduce the amount of sugar in his cake recipes. He decides to reduce the amount used in 1 cake by \(\frac12\) cup. He then uses \(4\frac12\) cups of sugar to bake 6 cakes.
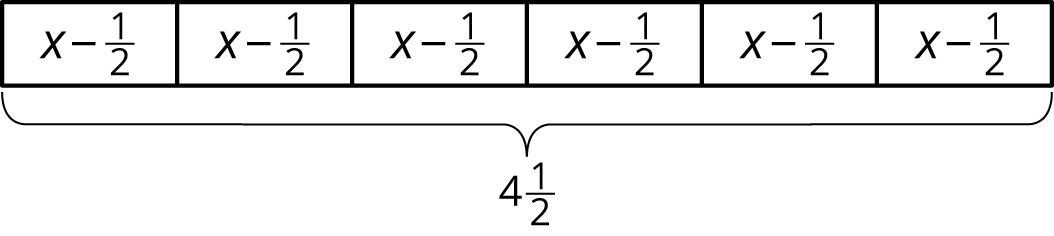
- Describe how the tape diagram represents the story.
- How much sugar was originally in each cake recipe?
Problem 7
One year ago, Clare was 4 feet 6 inches tall. Now Clare is 4 feet 10 inches tall. By what percentage did Clare’s height increase in the last year?