Lesson 11
Scales without Units
Let’s explore a different way to express scales.
11.1: One to One Hundred
A map of a park says its scale is 1 to 100.
- What do you think that means?
- Give an example of how this scale could tell us about measurements in the park.
11.2: Apollo Lunar Module
Your teacher will give you a drawing of the Apollo Lunar Module. It is drawn at a scale of 1 to 50.
- The “legs” of the spacecraft are its landing gear. Use the drawing to estimate the actual length of each leg on the sides. Write your answer to the nearest 10 centimeters. Explain or show your reasoning.
- Use the drawing to estimate the actual height of the Apollo Lunar Module to the nearest 10 centimeters. Explain or show your reasoning.
- Neil Armstrong was 71 inches tall when he went to the surface of the Moon in the Apollo Lunar Module. How tall would he be in the drawing if he were drawn with his height to scale? Show your reasoning.
- Sketch a stick figure to represent yourself standing next to the Apollo Lunar Module. Make sure the height of your stick figure is to scale. Show how you determined your height on the drawing.
The table shows the distance between the Sun and 8 planets in our solar system.
- If you wanted to create a scale model of the solar system that could fit somewhere in your school, what scale would you use?
- The diameter of Earth is approximately 8,000 miles. What would the diameter of Earth be in your scale model?
| planet | average distance (millions of miles) |
|---|---|
| Mercury | 35 |
| Venus | 67 |
| Earth | 93 |
| Mars | 142 |
| Jupiter | 484 |
| Saturn | 887 |
| Uranus | 1,784 |
| Neptune | 2,795 |
11.3: Same Drawing, Different Scales
A rectangular parking lot is 120 feet long and 75 feet wide.
- Lin made a scale drawing of the parking lot at a scale of 1 inch to 15 feet. The drawing she produced is 8 inches by 5 inches.
- Diego made another scale drawing of the parking lot at a scale of 1 to 180. The drawing he produced is also 8 inches by 5 inches.
- Explain or show how each scale would produce an 8 inch by 5 inch drawing.
- Make another scale drawing of the same parking lot at a scale of 1 inch to 20 feet. Be prepared to explain your reasoning.
- Express the scale of 1 inch to 20 feet as a scale without units. Explain your reasoning.
Summary
In some scale drawings, the scale specifies one unit for the distances on the drawing and a different unit for the actual distances represented. For example, a drawing could have a scale of 1 cm to 10 km.
In other scale drawings, the scale does not specify any units at all. For example, a map may simply say the scale is 1 to 1,000. In this case, the units for the scaled measurements and actual measurements can be any unit, so long as the same unit is being used for both. So if a map of a park has a scale 1 to 1,000, then 1 inch on the map represents 1,000 inches in the park, and 12 centimeters on the map represent 12,000 centimeters in the park. In other words, 1,000 is the scale factor that relates distances on the drawing to actual distances, and \(\frac{1}{1,\!000}\) is the scale factor that relates an actual distance to its corresponding distance on the drawing.
A scale with units can be expressed as a scale without units by converting one measurement in the scale into the same unit as the other (usually the unit used in the drawing). For example, these scales are equivalent:
-
1 inch to 200 feet
-
1 inch to 2,400 inches (because there are 12 inches in 1 foot, and \(200 \boldcdot 12 = 2,\!400\))
-
1 to 2,400
This scale tells us that all actual distances are 2,400 times their corresponding distances on the drawing, and distances on the drawing are \(\frac{1}{2,\!400}\) times the actual distances they represent.
Video Summary
Glossary Entries
- scale
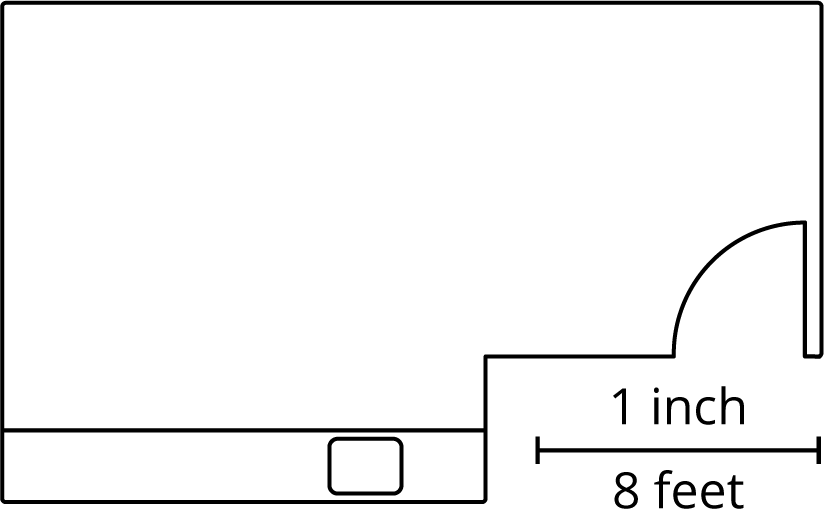
A scale tells how the measurements in a scale drawing represent the actual measurements of the object.
For example, the scale on this floor plan tells us that 1 inch on the drawing represents 8 feet in the actual room. This means that 2 inches would represent 16 feet, and \(\frac12\) inch would represent 4 feet.
- scale drawing
A scale drawing represents an actual place or object. All the measurements in the drawing correspond to the measurements of the actual object by the same scale.
