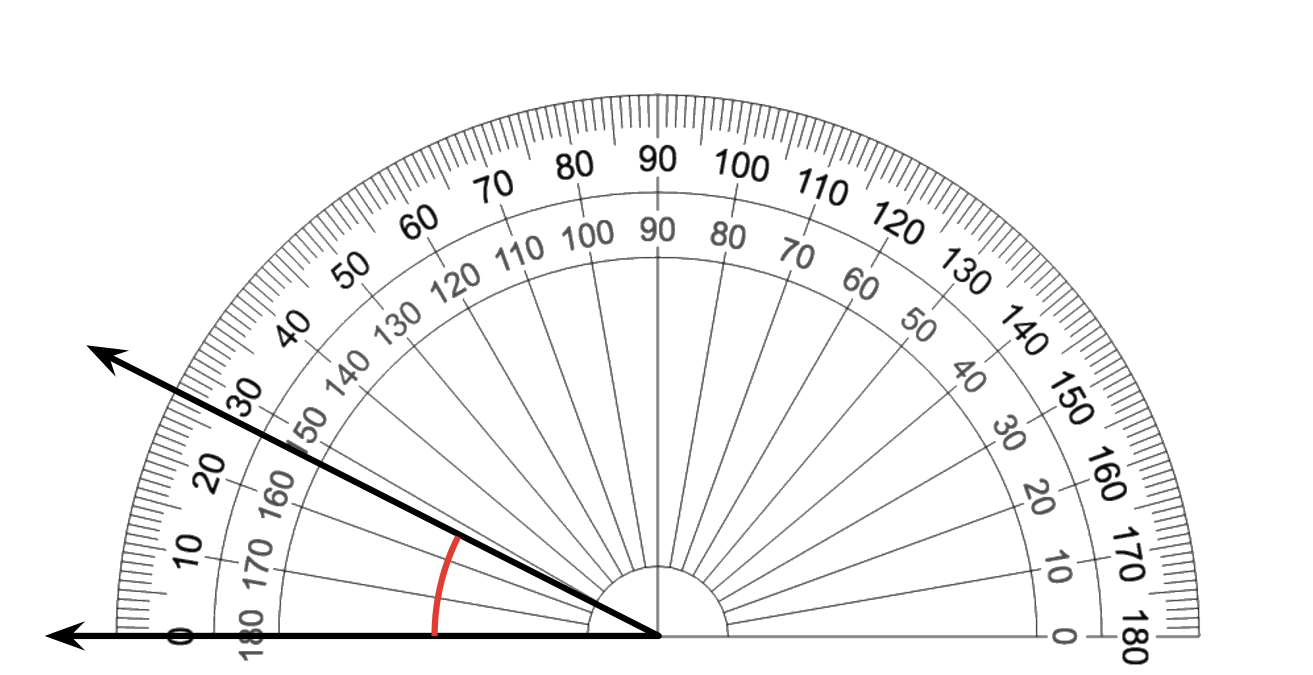
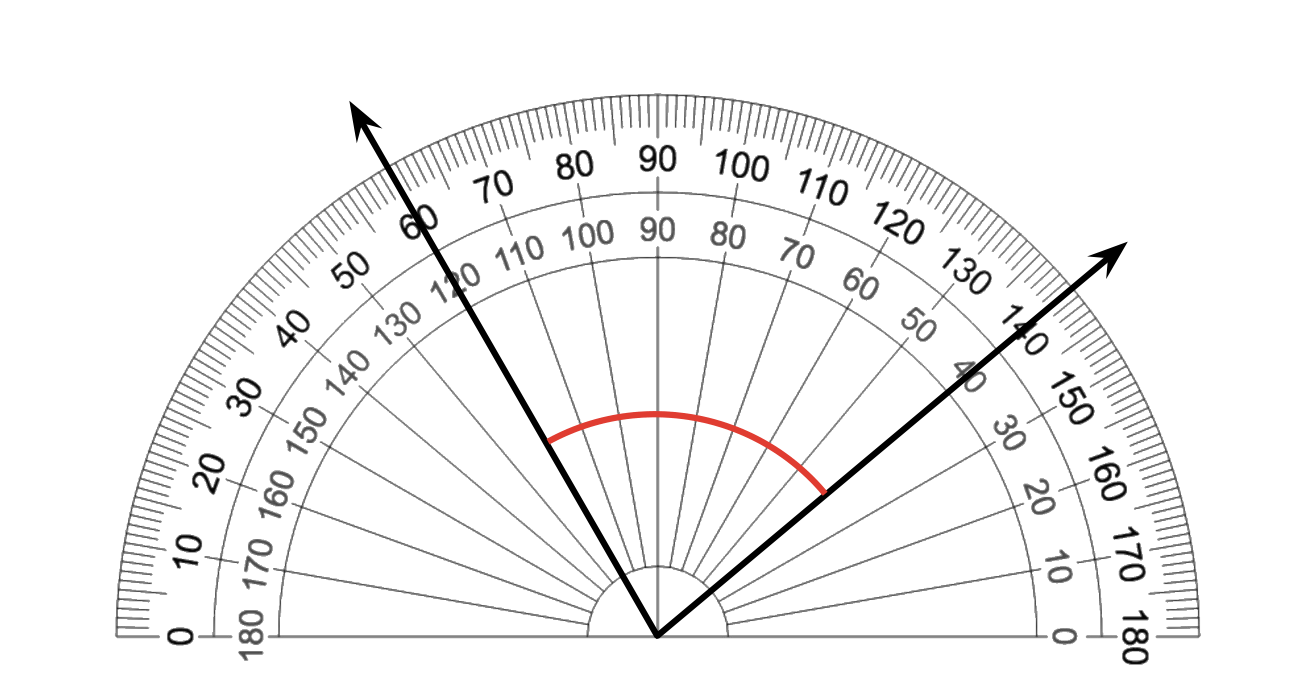
4.7 Angles and Angle Measurement

Unit Goals

  • Students learn to draw and identify points, rays, segments, angles, and lines, including parallel and perpendicular lines. Students also learn how to use a protractor to measure angles and draw angles of given measurements, and identify acute, obtuse, right, and straight angles in two-dimensional figures.

Section A Goals

  • Draw and identify points, lines, rays, segments, and parallel and intersecting lines in geometric figures.
  • Recognize that angles are formed wherever two rays share a common endpoint and identify angles in two-dimensional figures.

Section B Goals

  • Recognize that angles can be measured in degrees, and can be found using addition and subtraction.
  • Use a protractor to measure and draw angles, and recognize that perpendicular lines meet or cross at a right angle.

Section C Goals

  • Draw and identify acute, obtuse, right, and straight angles in two-dimensional figures.
  • Write equations to represent angle relationships and reason about and find unknown measurements.
Read More

Section A: Points, Lines, Segments, Rays, and Angles

Problem 1

Pre-unit

Practicing Standards:  3.G.A.1

Draw a rectangle on the grid and label it A. Draw a triangle and label it B. Draw a hexagon and label it C.

blank dot paper

Solution

For access, consult one of our IM Certified Partners.

Problem 2

Pre-unit

Practicing Standards:  3.G.A.1

  1. Is the shape a rhombus? Explain your reasoning.

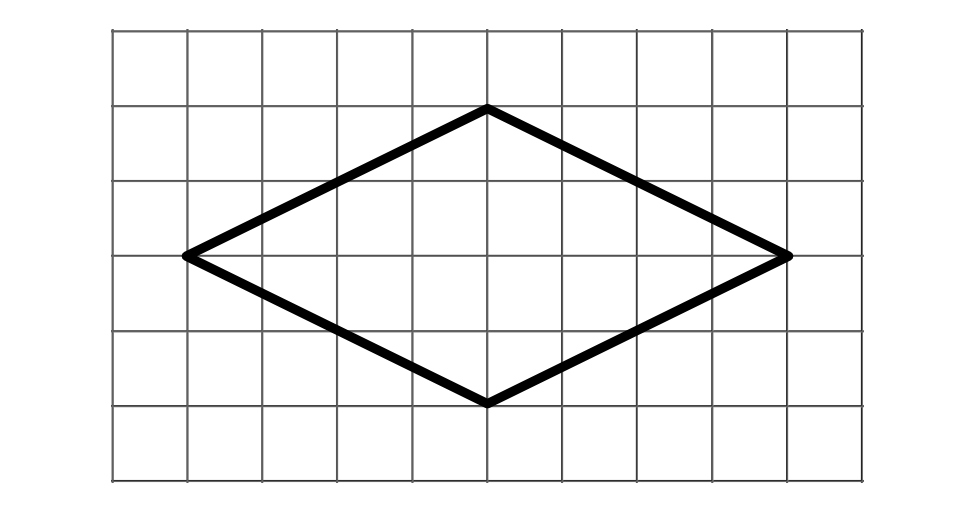
    4 sided shape on grid. all sides have the same length, corners are not square.
  2. Is the shape a rectangle? Explain your reasoning.
  3. Is the shape a square? Explain your reasoning.

Solution

For access, consult one of our IM Certified Partners.

Problem 3

  1. Draw 4 different lines through points on the grid. At least two of the lines should cross another line.
    image of dot paper
  2. Mark at least 3 different segments in your drawing.

Solution

For access, consult one of our IM Certified Partners.

Problem 4

  1. Circle the line segments that make up the letter A.

    image of the letter A on dot paper created by 3 segments
  2. Draw 4 rays that surround a rectangle.
  3. Can you find 4 different rays that surround the same rectangle?

Solution

For access, consult one of our IM Certified Partners.

Problem 5

Andre says that these two lines are parallel because they do not intersect.
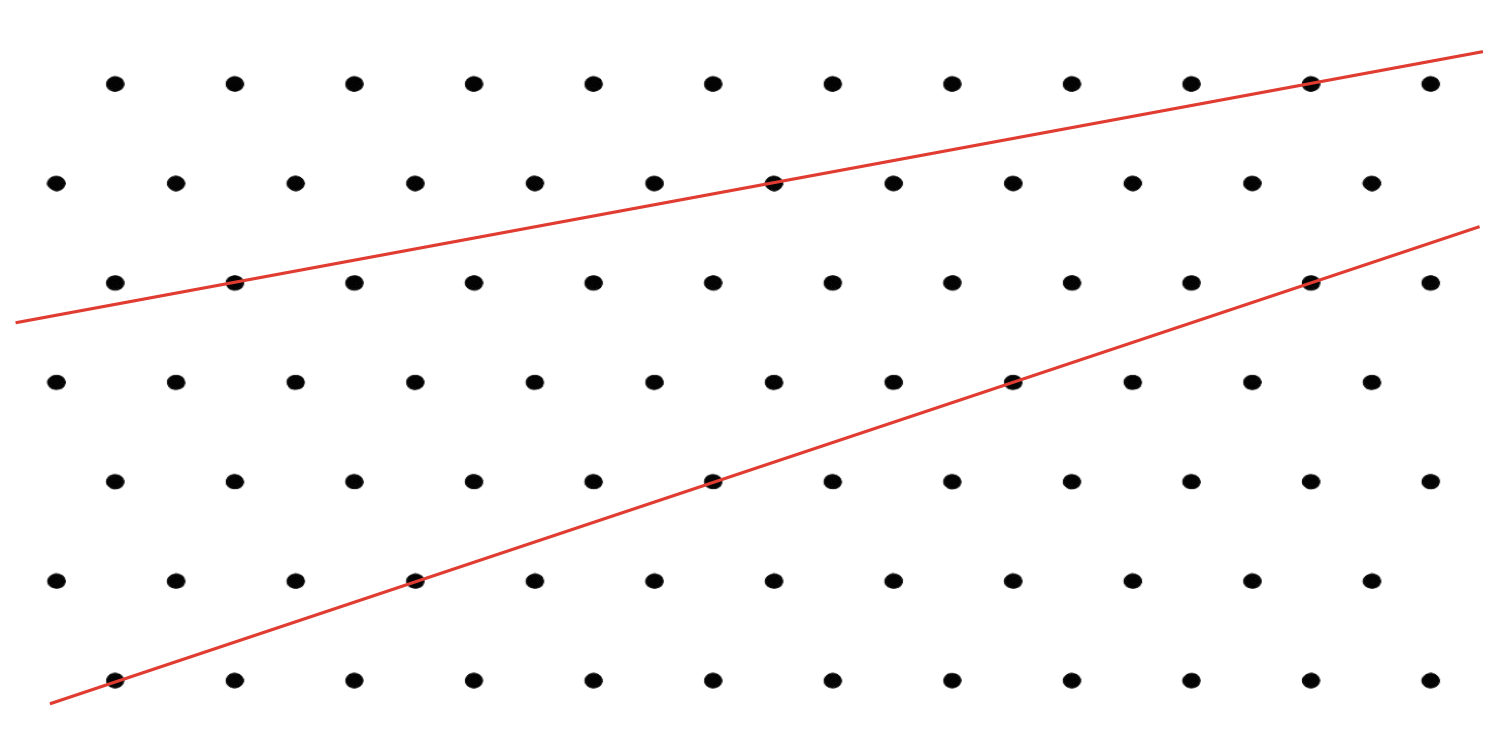
dot paper drawing. 2 lines slanted at different angles.
  1. Explain why Andre is not correct.
  2. Draw a line that is parallel to one of the lines in the image.

Solution

For access, consult one of our IM Certified Partners.

Problem 6

  1. Which segments of the letter Z are a pair of parallel lines? Draw the lines.
  2. Sketch a line that is parallel to the third segment in the Z.
image of the letter z

Solution

For access, consult one of our IM Certified Partners.

Problem 7

 

triangle. two acute angles and one angle about 90 degrees

  1. Find one angle in the figure. Draw a pair of rays to show the angle and extend them as far as you can.
  2. Find another angle in the figure. Draw a pair of rays to show it. Extend the rays as far as you can. (If you’d like, you can use a different colored pencil for this pair of rays.)
  3. Now that you have drawn some rays, do you see other angles that you didn’t see before? If you see one or more, label each one with a letter.

Solution

For access, consult one of our IM Certified Partners.

Problem 8

Exploration

Here is a riddle. Can you solve it?

“I am a capital letter made of more than 1 segment with no curved parts. I have no perpendicular segments or parallel segments. What letter could I be?”

Solution

For access, consult one of our IM Certified Partners.

Problem 9

Exploration

painting of a person. There are different sets of lines visible within the painting.
  1. Name or describe any shapes that you recognize in the painting.
  2. Do you see any parallel lines? If so, trace or circle them. (If you’d like, you can use a different colored pencil for each set of parallel lines.)
  3. Are there any angles in the painting? If so, mark them or describe where they are.

Solution

For access, consult one of our IM Certified Partners.

Section B: The Size of Angles

Problem 1

A
B

  1. Write two statements that compare the size of angles A and B.
  2. Draw an angle C that is bigger than both angle A and angle B.

Solution

For access, consult one of our IM Certified Partners.

Problem 2

A
B

  1. Which set of clock hands make a greater angle? Explain how you know.
  2. Choose one of the clocks and describe how to use the clock to draw the angle represented by the hands on the clock.

Solution

For access, consult one of our IM Certified Partners.

Problem 3

This angle has a measure of \(10^\circ\).

 
  1. How many of these angles can you put together, without overlaps, to make a complete circle? Explain or show how you know.
  2. Explain how you can use the given angle to sketch a \(5^\circ\) angle.

Solution

For access, consult one of our IM Certified Partners.

Problem 4

Use the given protractor to find the measurement of each angle.

  1. protractor measuring an angle. Left side at 0 or 1 hundred 80 degrees. Right side at 27 or 1 hundred 53 degrees.

  2. protractor measuring an angle. Left side at 45 or 1 hundred 35 degrees. Right side at 1 hundred 80 or 0 degrees.

  3. protractor measuring an angle. Left side at 60 or 1 hundred 20 degrees. Right side at 1 hundred 40 or 40 degrees.

Solution

For access, consult one of our IM Certified Partners.

Problem 5

Which of these shapes have segments that are perpendicular to one another? Trace or circle the perpendicular segments.

image of 3 geometric shapes.

Solution

For access, consult one of our IM Certified Partners.

Problem 6

Draw a ray. How many different \(35^\circ\) angles can you make using your ray and another ray? Explain your reasoning and make the angles.

Solution

For access, consult one of our IM Certified Partners.

Problem 7

Exploration

What is the smallest angle you can draw?

  1. Can you draw a \(10^\circ\) angle?
  2. What about a \(5^\circ\) angle or a \(1^\circ\) angle?
  3. What is difficult about drawing a small angle?

Solution

For access, consult one of our IM Certified Partners.

Problem 8

Exploration

  1. What are the measurements of the angles on the pentagon?
  2. Connect every pair of vertices of the pentagon with a line segment. What do you notice? What do you wonder?
pentagon. each angle equal, each side length equal.

Solution

For access, consult one of our IM Certified Partners.

Problem 9

Exploration

Can you estimate or find the measurement of the angle labeled \(f\)? If so, explain or show how you know.

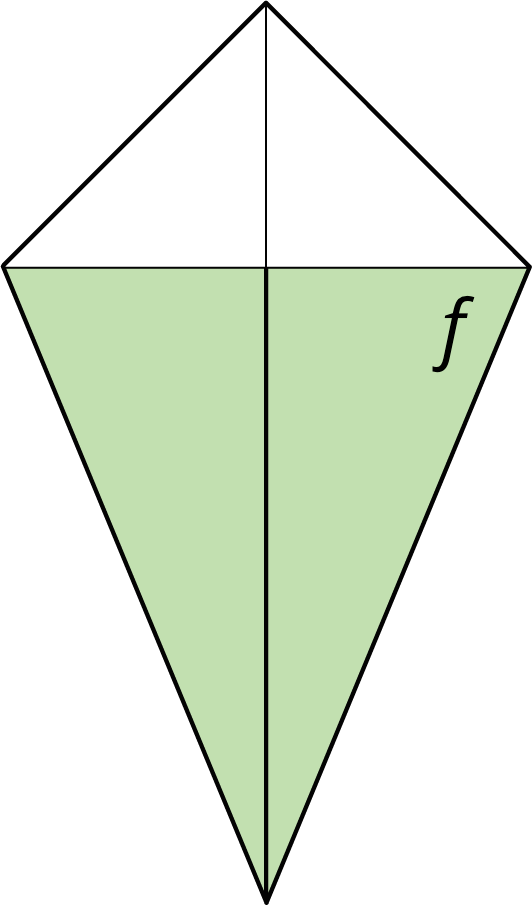
image of a kite. The angle located on the far right below the horizontal cross is labeled f.

Solution

For access, consult one of our IM Certified Partners.

Section C: Angle Analysis

Problem 1

  1. Draw an acute angle. Explain how you know the angle is acute.
  2. Extend one of the rays of your angle in the opposite direction. Explain why you’ve now created a new angle that is obtuse.

Solution

For access, consult one of our IM Certified Partners.

Problem 2

  1. The circle is divided into 12 equal parts. What is the measure of angle \(h\)?

    Explain or show how you know.

    circle partitioned into 12 equal parts. 1 part labeled h.
  2. Can you put together \(20^\circ\) angles to make a circle? How many of them will it take?

Solution

For access, consult one of our IM Certified Partners.

Problem 3

  1. A circle has been cut into eighths. How many degrees is the angle labeled \(m\)? Explain or show your reasoning.

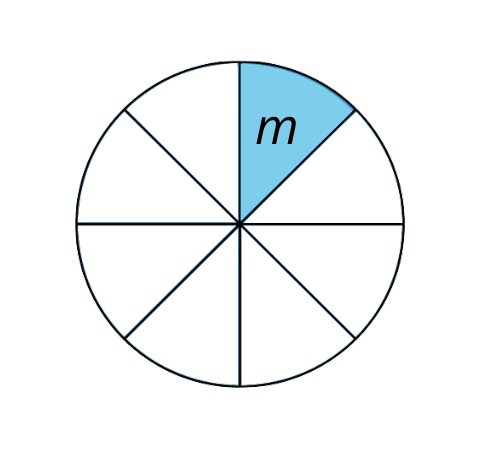
  2. Another circle has been cut into fifths. How many degrees is the angle labeled \(p\)? Explain or show your reasoning.

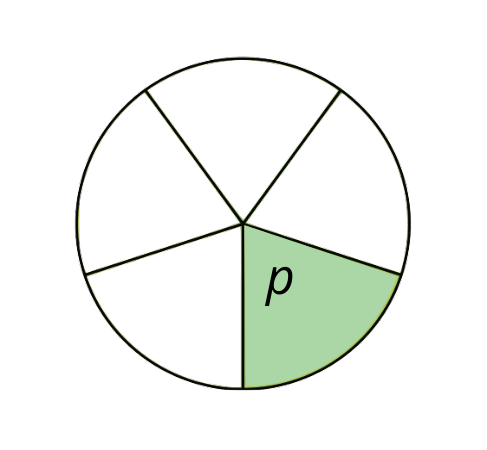
Solution

For access, consult one of our IM Certified Partners.

Problem 4

  1. What is the measure of each angle \(p\)? Explain or show how you know.

    1 right angle partitioned into 4 smaller angles. One angle labeled, 15 degrees. 3 angles labeled p.
  2. How many \(25^\circ\) angles can you fit together at one vertex without gaps or overlaps?

Solution

For access, consult one of our IM Certified Partners.

Problem 5

  1. What angles are made by the hour and minute hands on a clock at these times? Explain or show your reasoning.

    • 3:00

    • 5:00

    • 6:00

  2. How many degrees has the hour hand moved between 3:00 and 7:00? Explain or show how you know.

Solution

For access, consult one of our IM Certified Partners.

Problem 6

When Jada looked up at the clock, the long hand pointed at 12. Less than an hour later, she looked up again, and the long hand of the clock had turned 210 degrees. How many minutes had passed? Explain or show your reasoning.

Solution

For access, consult one of our IM Certified Partners.

Problem 7

Find the measure of each labeled angle in the drawing. Assume that:

  • The angles of the triangles meeting at the point in the middle of the figure are all the same.
  • The other angles of the triangles all have the same measure.
8 sided shape partitioned into 8 triangles of the same size.

Solution

For access, consult one of our IM Certified Partners.

Problem 8

In this diagram each angle on the left hand side is the same as the corresponding angle on the right hand side. Find the measure of angles \(x\), \(y\), and \(z\). Explain or show your reasoning.

diagram composed of shapes and angles.

Solution

For access, consult one of our IM Certified Partners.

Problem 9

Exploration

Tyler wonders if the hour hand and minute hand ever point in the same direction at the same time. Can you find some times when the hour hand and minute hand point in the same direction? Explain or show your reasoning.

Solution

For access, consult one of our IM Certified Partners.

Problem 10

Exploration

  1. Draw a rhombus with a \(50^\circ\) angle. Explain how you know your shape is a rhombus.
  2. Draw another rhombus with a \(50^\circ\) angle. How are your rhombuses the same? How are they different?

Solution

For access, consult one of our IM Certified Partners.

Problem 11

Exploration

How many degrees does the minute hand turn in each of the following times? Show how you know.

  1. 30 seconds
  2. 10 seconds
  3. 80 minutes
  4. 2.5 hours

Solution

For access, consult one of our IM Certified Partners.

Problem 12

Exploration

Here are diagrams of some pattern blocks. Each shape has some angles.

  1. How many angles do you see inside each shape?

    4 patterned blocks. From left to right, triangle, trapezoid, rhombus, hexagon.
    • a triangle
    • a trapezoid
    • a rhombus
    • a hexagon
  2. Here are diagrams of each type of blocks arranged around a shared point. 
    6 groups of pattern blocks connected around a central point.

    Use what you know about angle measurement to find the sizes of angles \(a\)–\(f\). Show your reasoning.

Solution

For access, consult one of our IM Certified Partners.