Scope and Sequence
Narrative
The big ideas in grade 4 include: developing understanding and fluency with multi-digit multiplication, and developing understanding of dividing to find quotients involving multi-digit dividends; developing an understanding of fraction equivalence, addition and subtraction of fractions with like denominators, and multiplication of fractions by whole numbers; understanding that geometric figures can be analyzed and classified based on their properties, such as having parallel sides, perpendicular sides, particular angle measures, and symmetry.
The mathematical work for grade 4 is partitioned into 9 units:
- Factors and Multiples
- Fraction Equivalence and Comparison
- Extending Operations to Fractions
- From Hundredths to Hundred-thousands
- Multiplicative Comparison and Measurement
- Multiplying and Dividing Multi-digit Numbers
- Angles and Angle Measurement
- Properties of Two-dimensional Shapes
- Putting it All Together
Unit 1: Factors and Multiples
Unit Learning Goals- Students apply understanding of multiplication and area to work with factors and multiples.
In this unit, students extend their knowledge of multiplication, division, and the area of a rectangle to deepen their understanding of factors and to learn about multiples.
In grade 3, students learned that they can multiply the two side lengths of a rectangle to find its area, and divide the area by one side length to find the other side length.
To represent these ideas, they used area diagrams, wrote expressions and equations, and learned the terms “factors” and “products.”

In this unit, students return to the concept of area to make sense of factors and multiples of numbers. Given a rectangle with a particular area, students find as many pairs of whole-number side lengths as they can. They make sense of those side lengths as factor pairs of the whole-number area, and the area as a multiple of each side length.
Students also learn that a number can be classified as prime or composite based on the number of factor pairs it has.
Throughout the unit, students encounter various contexts related to school, gatherings, and celebrations. They are intended to invite conversations about students’ lives and experiences. Consider them as opportunities to learn about students as individuals, to foster a positive learning community, and to shape each lesson based on insights about students.
Section A: Understand Factors and Multiples
Standards Alignments| Addressing | 4.OA.B.4, 4.OA.C.5 |
- Determine if a number is prime or composite.
- Explain what it means to be a factor or a multiple of a whole number.
- Relate the side lengths and area of a rectangle to factors and multiples.
In this section, students revisit the ideas of area and factors from grade 3 and encounter the idea of multiples. They begin by building rectangles given specific side lengths and identifying possible areas when only one side length is known. Students use tiles and diagrams to build their understanding before learning new terminology.
Next, students build rectangles given a certain area. They see that the side lengths of the rectangles represent the factor pairs of the given area value. Students also observe the commutative property of multiplication when they see that rectangles with the same pair of side lengths have the same area, regardless of their orientation.
Build 5 different rectangles with the given width. Record the area of each rectangle in the table.
| \(\hspace{1in}\)area of rectangle\(\hspace{1in}\) | |||||
|---|---|---|---|---|---|
| 2 tiles wide | |||||
| 3 tiles wide | |||||
| 4 tiles wide | |||||
Students discover that for some whole-number values of area, only one rectangle can be built, and for other values, more than one rectangle is possible. Likewise, some numbers have only one factor pair (the number itself and 1) and other numbers have more than one factor pair. Students learn that we call the former “prime numbers” and the latter “composite numbers.”
The section closes with an optional game day, which is an opportunity to see students' fluency with multiplication and division within 100.
PLC: Lesson 1, Activity 2, What Areas Can You Build?
Section B: Find Factor Pairs and Multiples
Standards Alignments| Addressing | 4.OA.A.3, 4.OA.B, 4.OA.B.4 |
- Apply multiplication fluency within 100 and the relationship between multiplication and division to find factor pairs and multiples.
In this section, students apply and deepen their understanding of the ideas of factors and multiples as they play games and solve problems in context. The activities prompt students to look for patterns in factors, multiples, and prime and composite numbers, and use them to make predictions and generalize their observations.
Twenty students are playing a game with 20 lockers in a row.
The first student starts with the first locker and opens all the lockers.
The second student starts at the second locker and shuts every other locker.
The third student stops at every third locker and opens it if it is closed or closes it if it is open.

Which locker numbers does the third student touch?
How many students touch locker 17?
In the last lesson, students have a chance to use the ideas from this unit to create geometric art.
PLC: Lesson 6, Activity 1, Questionable Lockers
Estimated Days: 6 - 8
Unit 2: Fraction Equivalence and Comparison
Unit Learning Goals- Students generate and reason about equivalent fractions and compare and order fractions with the following denominators: 2, 3, 4, 5, 6, 8, 10, 12, and 100.
In this unit, students extend their prior understanding of equivalent fractions and comparison of fractions.
In grade 3, students partitioned shapes into parts with equal area and expressed the area of each part as a unit fraction. They learned that any unit fraction \(\frac{1}{b}\) results from a whole partitioned into \(b\) equal parts. They used unit fractions to build non-unit fractions, including fractions greater than 1, and represent them on fraction strips and tape diagrams. The denominators of these fractions were limited to 2, 3, 4, 6, and 8. Students also worked with fractions on a number line, establishing the idea of fractions as numbers and equivalent fractions as the same point on the number line.
Here, students follow a similar progression of representations. They use fraction strips, tape diagrams, and number lines to make sense of the size of fractions, generate equivalent fractions, and compare and order fractions with denominators 2, 3, 4, 5, 6, 8, 10, 12, and 100.
Students generalize that a fraction \(\frac{a}{b}\) is equivalent to fraction \(\frac{(n \times a)}{(n \times b)}\) because each unit fraction is being broken into \(n\) times as many equal parts, making the size of the part \(n\) times as small \(\frac{1}{(n \times b)}\) and the number of parts in the whole \(n\) times as many \((n \times a)\). For example, we can see \(\frac{3}{5}\) is equivalent to \(\frac{6}{10}\) because when each fifth is partitioned into 2 parts, there are \(2 \times 3\) or 6 shaded parts, twice as many as before, and the size of each part is half as small, \(\frac{1}{(2 \times 5)}\) or \(\frac{1}{10}\).


As the unit progresses, students use equivalent fractions and benchmarks such as \(\frac{1}{2}\) and 1 to reason about the relative location of fractions on a number line, and to compare and order fractions.
Section A: Size and Location of Fractions
Standards Alignments| Addressing | 4.NF.A.1, 4.NF.A.2 |
- Make sense of fractions with denominators 2, 3, 4, 5, 6, 8, 10, and 12 through physical representations and diagrams.
- Reason about the location of fractions on the number line.
In this section, students revisit ideas and representations of fractions from grade 3, working with denominators that now include 5, 10, and 12. They use physical fraction strips, diagrams of fraction strips, tape diagrams, and number lines to make sense of the size of fractions and fractional relationships.
Students reason about the relationship between fractions where one denominator is a multiple of the other denominator (such as \(\frac{1}{5}\) and \(\frac{1}{10}\), or \(\frac{1}{6} \) and \(\frac{1}{12}\)). They consider different ways to represent these relationships. Students also compare fractions to benchmarks such as \(\frac{1}{2}\) and 1.


The work in this section prepares students to reason about equivalence and comparison of fractions in the subsequent lessons.
PLC: Lesson 4, Activity 2, Fractions on Number Lines
Section B: Equivalent Fractions
Standards Alignments| Addressing | 4.NF.A.1 |
- Generate equivalent fractions with the following denominators: 2, 3, 4, 5, 6, 8, 10, 12, and 100.
- Use visual representations to reason about fraction equivalence, including using benchmarks such as $\frac{1}{2}$ and 1.
In this section, students develop their ability to reason about and generate equivalent fractions. They begin by using number lines as a tool for finding equivalent fractions and verifying equivalence of two fractions.


Through repeated reasoning, students notice regularity in the visual representations and begin to make sense of a numerical way to determine equivalence and generate equivalent fractions (MP8). They generalize that fraction \(\frac{a}{b}\) is equivalent to fraction \(\frac{n \times a}{n \times b} \).
Note that students do not need to describe this generalization in algebraic notation. Given their understanding of the size of fractions and relationship between fractions, however, they should be able to explain it with fractions that have denominators 2, 3, 4, 5, 6, 8, 10, 12, and 100.
As they identify and generate equivalent fractions numerically, students apply their knowledge of factors and multiples from an earlier unit.
PLC: Lesson 8, Activity 1, Handy Number Lines
Section C: Fraction Comparison
Standards Alignments| Addressing | 4.NF.A, 4.NF.A.1, 4.NF.A.2 |
- Use visual representations or a numerical process to reason about fraction comparison.
By the time they reach this section, students have an expanded set of understandings and strategies for reasoning about the size of fractions. Here, they further develop these skills and work to compare fractions with different numerators and different denominators.
To make comparisons, students may use visual representations, equivalent fractions, and their understanding of the size of fractions (for instance, relative to benchmarks such as \(\frac{1}{2}\) and 1). They may rely on the meaning of the numerator and denominator, and choose a way to compare based on the numbers at hand. Students record the results of comparisons with symbols \(<\), \(=\), or \(>\).
At the end of the section, students learn to write equivalent fractions with a particular denominator as a way to compare any fractions, another opportunity to apply the idea of factors and multiples. Having a numerical strategy notwithstanding, students are still encouraged to use flexible methods to reason about the relative size of fractions.
PLC: Lesson 12, Activity 1, The Greatest of Them All
Estimated Days: 16 - 17
Unit 3: Extending Operations to Fractions
Unit Learning Goals- Students learn that a fraction $\frac{a}{b}$ is a product of a whole number $a$ and a unit fraction $\frac{1}{b}$, or $\frac{a}{b} = a \times \frac{1}{b}$, and that $n \times \frac{a}{b} = \frac{(n \space \times \space a)}{b}$. Students learn to add and subtract fractions with like denominators, and to add and subtract tenths and hundredths.
In this unit, students deepen their understanding of how fractions can be composed and decomposed, and learn about operations on fractions.
In grade 3, students partitioned a whole into equal parts and identified one of the parts as a unit fraction. They learned that non-unit fractions and whole numbers are composed of unit fractions. They used visual fraction models, including tape diagrams and number lines, to represent and compare fractions. In a previous unit, students extended that work and reasoned about fraction equivalence.
Here, students multiply fractions by whole numbers, add and subtract fractions with the same denominator, and add tenths and hundredths. They rely on familiar concepts and representations to do so. For instance, students had represented multiplication on a tape diagram, with equal-size groups and a whole number in each group. Here, they use a tape diagram that shows a fraction in each group.
\(3 \times \frac{1}{5} = \frac{3}{5}\)

In earlier grades, students used number lines to represent addition and subtraction of whole numbers. Here, they use number lines to represent the decomposition of fractions into sums, and to reason about addition and subtraction of fractions with the same denominator, including mixed numbers.
\( \frac{4}{3} + \frac{6}{3} = \frac{10}{3}\)

\(\frac{11}{6} – \frac{7}{6} = \frac{4}{6}\)

Students then apply these skills in the context of measurement and data. They analyze line plots showing fractional lengths and find sums and differences to answer questions about the data.
Lastly, students use fraction equivalence to find sums of tenths and hundredths. For instance, to find \(\frac{3}{10} + \frac{15}{100}\), they reason that \(\frac{3}{10}\) is equivalent to \(\frac{30}{100}\), so the sum is \(\frac{30}{100} + \frac{15}{100}\), which is \(\frac{45}{100}\).
Section A: Equal Groups of Fractions
Standards Alignments| Addressing | 4.NF.B.4, 4.NF.B.4.a, 4.NF.B.4.b, 4.NF.B.4.c |
- Recognize that $n \times \frac{a}{b} = \frac{(n \space \times \space a)}{b}$.
- Represent and explain that a fraction $\frac{a}{b}$ is a multiple of $\frac{1}{b}$, namely $a \times \frac{1}{b}$.
- Represent and solve problems involving multiplication of a fraction by a whole number.
In this section, students extend their earlier understanding of multiplication as equal groups of whole numbers of objects to now include equal groups of fractional pieces.
How many do you see? How do you see them?

Students begin by reasoning about groups containing unit fractions. For instance, they interpret the 5 plates with half an orange each as \(5 \times \frac{1}{2}\), which is \(\frac{5}{2}\). Later, they also reason about groups of non-unit fractions and write expressions to represent the quantities. For instance, 5 groups of \(\frac{3}{4}\) can be expressed as \(5 \times \frac{3}{4}\) or \(\frac{15}{4}\).
Later, students reason with diagrams and equations. Through repeated reasoning, they see regularity in the product of a whole number and a fraction (MP8). The numerator in the resulting fraction is the product of the whole number and the numerator of the fractional factor, and the denominator is the same as in the fractional factor.
\(4 \times \frac{2}{3} = \frac{8}{3}\)

These diagrams also help students see that some fractions can be represented by more than one multiplication expression. Students can reason that \(\frac{8}{3}\) is \(8 \times \frac{1}{3}\), which is also equivalent to \(4 \times 2 \times \frac{1}{3}\) and \(2 \times 4 \times \frac{1}{3}\), and is therefore equivalent to \(4 \times\frac{2}{3}\) and \(2 \times\frac{4}{3}\), respectively.
By circling the diagram in various ways, students can visualize the different combinations of groups, understand their equivalence, and observe the associative property of multiplication. In doing this work, students practice looking for and making use of structure (MP7).
Students then solve problems that involve fraction multiplication, using diagrams and equations to show their reasoning. These diagrams will also be useful in later grades, when students make sense of fractions as quotients.
PLC: Lesson 2, Activity 1, Card Sort: Expressions and Diagrams
Section B: Addition and Subtraction of Fractions
Standards Alignments| Addressing | 4.MD.B.4, 4.NF.B.3, 4.NF.B.3.a, 4.NF.B.3.b, 4.NF.B.3.c, 4.NF.B.3.d, 4.NF.B.4.c |
- Create and analyze line plots that display measurement data in fractions of a unit ($\frac18, \frac14, \frac12$).
- Represent and solve problems that involve the addition and subtraction of fractions and mixed numbers, including measurements presented in line plots.
- Use various strategies to add and subtract fractions and mixed numbers with like denominators.
In this section, students learn to add and subtract fractions by decomposing them into sums of smaller fractions, writing equivalent fractions, and using number lines to support their reasoning.
Students begin by thinking about a fraction as a sum of unit fractions with the same denominator and then as a sum of other smaller fractions. They represent different ways to decompose a fraction by drawing “jumps” on number lines and writing different equations.
\(\frac{13}{10} = \frac{10}{10} + \frac{3}{10}\)

\(\frac{13}{10} = \frac{5}{10} + \frac{8}{10}\)

Working with number lines helps students see that a fraction greater than 1 can be decomposed into a whole number and a fraction, and then be expressed as a mixed number. This can in turn help us add and subtract fractions with the same denominator. For example, to find the value of \(3 - \frac{2}{5}\), it helps to first decompose the 3 into \(2 + \frac{5}{5}\), and then subtract \(\frac{2}{5}\) from the \(\frac{5}{5}\).
Later in the section, students organize fractional length measurements (\(\frac{1}{2}\), \(\frac{1}{4}\), and \(\frac{1}{8}\) inch) on line plots. They apply their ability to interpret line plots and to add and subtract fractions to solve problems about measurement data.
What is the difference between the largest and smallest shoe lengths?
Explain or show your reasoning.

PLC: Lesson 10, Activity 1, What’s Left?
Section C: Addition of Tenths and Hundredths
Standards Alignments| Addressing | 4.NF.A.1, 4.NF.A.2, 4.NF.B.3.c, 4.NF.B.3.d, 4.NF.B.4, 4.NF.B.4.c, 4.NF.C.5 |
- Reason about equivalence to add tenths and hundredths.
- Reason about equivalence to solve problems involving addition and subtraction of fractions and mixed numbers.
In this section, students apply their understanding of fraction equivalence to add tenths and hundredths.
In the previous unit, students learned that \(\frac{1}{10} = \frac{10}{100}\). They use this reasoning to add tenths and hundredths by generating equivalent fractions. They also apply what they learned in the previous section to strategically use decomposition and the associative and commutative properties to add three or more tenths and hundredths, including mixed numbers.
This section ends with an optional lesson that allows students to apply what they have learned about multiplication, addition, and subtraction of fractions and mixed numbers to solve a design problem.
PLC: Lesson 15, Activity 2, Stacks of Blocks
Estimated Days: 18 - 20
Unit 4: From Hundredths to Hundred-thousands
Unit Learning Goals- Students read, write and compare numbers in decimal notation. They also extend place value understanding for multi-digit whole numbers and add and subtract within 1,000,000.
In this unit, students learn to express both small and large numbers in base ten, extending their understanding to include numbers from hundredths to hundred-thousands.
In previous units, students compared, added, subtracted, and wrote equivalent fractions for tenths and hundredths. Here, they take a closer look at the relationship between tenths and hundredths and learn to express them in decimal notation. Students analyze and represent fractions on square grids of 100 where the entire grid represents 1. They reason about the size of tenths and hundredths written as decimals, locate decimals on a number line, and compare and order them.
Students then explore large numbers. They begin by using base-ten blocks and diagrams to build, read, write, and represent whole numbers beyond 1,000. Students see that ten-thousands are related to thousands in the same way that thousands are related to hundreds, and hundreds are to tens, and tens are to ones.
As they make sense of this structure (MP7), students see that the value of the digit in a place represents ten times the value of the same digit in the place to its right.
Students then reason about the size of multi-digit numbers and locate them on number lines. To do so, they need to consider the value of the digits. They also compare, round, and order numbers through 1,000,000. They also use place-value reasoning to add and subtract numbers within 1,000,000 using the standard algorithm.
Throughout the unit, students relate these concepts to real-world contexts and use what they have learned to determine the reasonableness of their responses.
Section A: Decimals with Tenths and Hundredths
Standards Alignments| Addressing | 4.NF.C, 4.NF.C.5, 4.NF.C.6, 4.NF.C.7 |
- Represent, compare, and order decimals to the hundredths by reasoning about their size.
- Write tenths and hundredths in decimal notation.
Previously, students learned that there are 10 hundredths in 1 tenth and explored tenths and hundredths in fraction notation. In this section, they learn to represent and reason about tenths and hundredths in decimal notation.
Students relate \(\frac{1}{10}\) to the notation 0.1 and \(\frac{1}{100}\) to 0.01. They learn to read 0.1 as “one tenth” and 0.01 as “one hundredth,” the same way these numbers are called when written in fraction notation. To see the connections between the fraction notation, decimal notation, and the word name, students reason with unit squares (representing 1) divided into hundredths.
The squares in this section are shaded from left to right, to reflect the digits in a decimal. For example, the number 1.33 is represented by shading a full square that represents 1, 3 columns in the next large square, and 3 small squares in the adjacent column.

The structure of the unit square grid helps to illustrate the equivalence of \(\frac{10}{100}\) and \(\frac{1}{10}\). It also allows students to see that 0.10 is equivalent to 0.1, and to generalize it to other equivalent tenths and hundredths, for instance \(0.20 = 0.2\) and \(0.5 = 0.50\).
In these materials, decimals less than 1 are expressed with a leading zero. Consider explaining to students the zero is sometimes omitted and this doesn’t impact the value of the decimal.
Later in the section, students use benchmarks such as 0.5 and the relationship between tenths and hundredths to locate and label decimals on a number line. They compare and order decimals based on size and write comparison statements using the symbols <, >, and =.

PLC: Lesson 3, Activity 1, Points on Number Lines
Section B: Place-value Relationships through 1,000,000
Standards Alignments| Addressing | 4.NBT.A.1, 4.NBT.A.2, 4.NBT.B.4 |
- Read, represent, and describe the relative magnitude of multi-digit whole numbers up to 1 million.
- Recognize that in a multi-digit whole number, the value of a digit in one place represents ten times what it represents in the place to its right.
In this section, students make sense of whole numbers up to the hundred-thousands place, learn to read and write them, and deepen their understanding of place value.
Students begin by using base-ten blocks and diagrams to represent and reason about multi-digit numbers. They quickly see the limits of using base-ten blocks to represent large numbers when the smallest cube represents 1. For example, this collection represents 1,325. If the smallest block has a value of 10 or ten times as much, however, the same collection would represent 13,250. The reasoning here prepares them to think about place-value relationships.

As students analyze and draw base-ten diagrams and write multi-digit numbers in expanded form, they observe structure and begin to understand the value of the digit in each position (MP7). They see the “ten times” relationship between the value of a digit in one place and that of the same digit in a place to its right. For example, \(300,\!000 = 10 \times 30,\!000\), so the 3 in 347,000 has a value ten times that of the 3 in 34,700.
Students also see this “ten times” relationship as they locate numbers on a number line. If the endpoints of a number line are each ten times those on another number line, points that are in the same position on the two number lines are related by a factor of 10 as well.




Students use these observations of structure to compare, order, and round numbers in the next section.
PLC: Lesson 6, Activity 2, What is 10,000?
Section C: Compare, Order, and Round
Standards Alignments| Addressing | 4.NBT.A.2, 4.NBT.A.3 |
- Compare, order, and round multi-digit whole numbers within 1,000,000.
In grade 3, students compared, ordered, and rounded numbers within 1,000. In this section, they extend that work to include numbers within 1,000,000.
Students begin by placing multi-digit numbers on a number line with increasing levels of precision and then making comparisons. In comparing numbers, including those that are missing digits in some places, they make use of structure to determine the size of numbers and the significance of the value of the digits (MP7).
Is it possible to fill in the two blanks with the same digit to make:
\(\boxed{4} \ \boxed{\phantom{0}} \ , \boxed{3} \ \boxed{0} \ \boxed{0}\) less than \(\boxed{3} \ \boxed{\phantom{0}} \ , \boxed{4} \ \boxed{0} \ \boxed{0}\) ?
\(\boxed{\phantom{0}} \ \boxed{4} \ , \boxed{3} \ \boxed{0} \ \boxed{0}\) less than \(\boxed{\phantom{0}} \ \boxed{3} \ , \boxed{4} \ \boxed{0} \ \boxed{0}\)?
Previously, students rounded numbers to the nearest multiple of 10 or 100. Here, they round numbers within 1,000,000 to the nearest multiples of 10, 100, 1,000, 10,000, and 100,000. When a number is exactly halfway between two consecutive multiples of 1,000, 10,000, or 100,000, they round up, following the convention used in grade 3 when rounding to the nearest multiple of 10 or 100.
Students apply their understanding of place value and rounding to solve contextual problems. They also engage in aspects of mathematical modeling as they consider the implications of rounding large numbers in different situations (MP4).
PLC: Lesson 16, Activity 1, Round to What?
Section D: Add and Subtract
Standards Alignments| Addressing | 4.NBT.A, 4.NBT.A.2, 4.NBT.B.4, 4.NF.B.3.c |
- Add and subtract multi-digit whole numbers using the standard algorithm.
In grade 3, students used various representations and strategies to add and subtract within 1,000, including strategies that rely on place value. In this section, they build on those strategies while also learning about the standard algorithm for addition and subtraction. They begin working toward the end-of-grade expectation of fluency with addition and subtraction within 1,000,000.
As in earlier grades, students attend to the relationship between addition and subtraction, and find sums and differences by composing and decomposing numbers. They compare an algorithm that uses expanded form and the standard algorithm, and observe the role of place value in both algorithms.


Students start by finding sums that do not require composing a unit in any given place and progress towards those that require composing a unit multiple times.
Likewise, they start by subtracting numbers that don’t require decomposing a unit and move towards differences that require multiple decompositions. Students practice adding and subtracting numbers both in and out of context.

PLC: Lesson 20, Activity 1, Add and Subtract Large Numbers
Estimated Days: 22 - 23
Unit 5: Multiplicative Comparison and Measurement
Unit Learning Goals- Students interpret, represent, and solve multiplicative comparison problems using an understanding of the relationship between multiplication and division. They use this thinking to convert units of measure within a given system from larger to smaller units.
In this unit, students make sense of multiplication as a way to compare quantities. They use this understanding to solve problems about measurement.
In earlier grades, students related two quantities and made additive comparison, where the key question was “How many more?” Here, they make multiplicative comparison, in which the underlying question is “How many times as many?” For example, if Mai has 3 cubes and Tyler has 18 cubes, we can say that Tyler has 6 times as many cubes as Mai does.
Initially, students reason using concrete manipulatives and discrete images. Later, they reason more abstractly, using tape diagrams and equations. Comparative language such as “_____ times as many (or much) as ____” is emphasized, offering students opportunities to attend to precision as they communicate mathematically (MP6).
Write a multiplication equation to compare
the pages read by Elena and Clare.
Use a symbol to represent the unknown.

Next, students use the idea and language of multiplicative relationships to learn about various units of length, mass, capacity, and time, and to convert from larger units to smaller units within the same system of measurement. For example, they describe 1 kilometer as 1,000 times as long as a meter. Students then use their new knowledge to solve measurement problems.

Elena’s frisbee went 3 times as far as Clare’s did.
Andre’s frisbee went 4 times as far as Tyler’s did.
How far did Elena and Tyler throw the frisbee?
| student | distance |
|---|---|
| Han | 17 yards |
| Lin | \(51\frac{1}{2}\) feet |
| Clare | \(21 \frac{1}{3}\) feet |
| Andre | 22 yards 2 feet |
| Elena | |
| Tyler |
Section A: Multiplicative Comparison
Standards Alignments| Addressing | 4.NBT.B.5, 4.OA.A.1, 4.OA.A.2, 4.OA.A.3 |
- Analyze, describe, and represent multiplicative comparison situations.
- Solve one-step and two-step problems involving multiplicative comparison.
In this section, students learn to compare two quantities in terms of multiplication and to solve multiplicative comparison problems.
In earlier grades, students made comparisons in terms of addition or subtraction. To describe the number of cubes in the image, they may say, “Han has 3 more cubes than Andre,” or “Andre has 3 fewer cubes than Han.” Here, they make this comparison by saying “Han has 2 times (or twice) as many cubes as Andre.”

Students begin with comparisons that involve small factors and familiar situations (such as comparing blocks), using familiar multiplicative comparison language (such as “twice,” or “twice as many”). They progress from using concrete representations (actual cubes) to discrete diagrams (showing cubes, or showing sections that each represent single objects). As they encounter larger factors and more-abstract situations, students interpret and use diagrams where each section represents any quantity.
Diego has 5 times as many cubes as Kiran.

Diego read 8 times as many books as Lin. Lin read 7 books. How many books did Diego read?

Students write multiplication equations to express comparisons. As the problems become more complex, they reason with given diagrams (or diagrams they draw) and use division to find a missing factor.
Jada read some pages. Han read 60 pages altogether. The diagram shows how their pages compare.
How many times as many as Jada's pages did Han read?

PLC: Lesson 2, Activity 2, Diagrams to Solve Multiplicative Comparison Problems
Section B: Measurement Conversion
Standards Alignments| Addressing | 4.MD.A.1, 4.MD.A.2, 4.OA.A.2, 4.OA.A.3 |
- Convert from larger units to smaller units within a given system of measurement.
- Solve multi-step problems involving multiplicative comparison and measurement.
- Understand the relative sizes of kilometers, meters and centimeters, liters and milliliters, kilograms and grams, and pounds and ounces.
Students have encountered units of measurement in earlier grades and in their daily lives. They have measured and estimated lengths in centimeters and meters, recognized the number of minutes in an hour and measured intervals of time, and solved problems involving capacity and mass.
In this section, students expand on these concepts to convert measurements within the same system (metric or customary) from larger units to smaller units. These conversions require an understanding of the multiplicative relationship between units.
Students begin by exploring lengths in metric units. To develop a sense of the multiplicative relationship between centimeters and meters, students build a length of 1 meter from centimeter grid paper. They recognize that 1 meter is 100 times as long as 1 centimeter and use this reasoning to convert meters to centimeters. Later, they make sense of 1 kilometer by relating it to multiples of shorter measurements, such as the length of a basketball court or a soccer field.
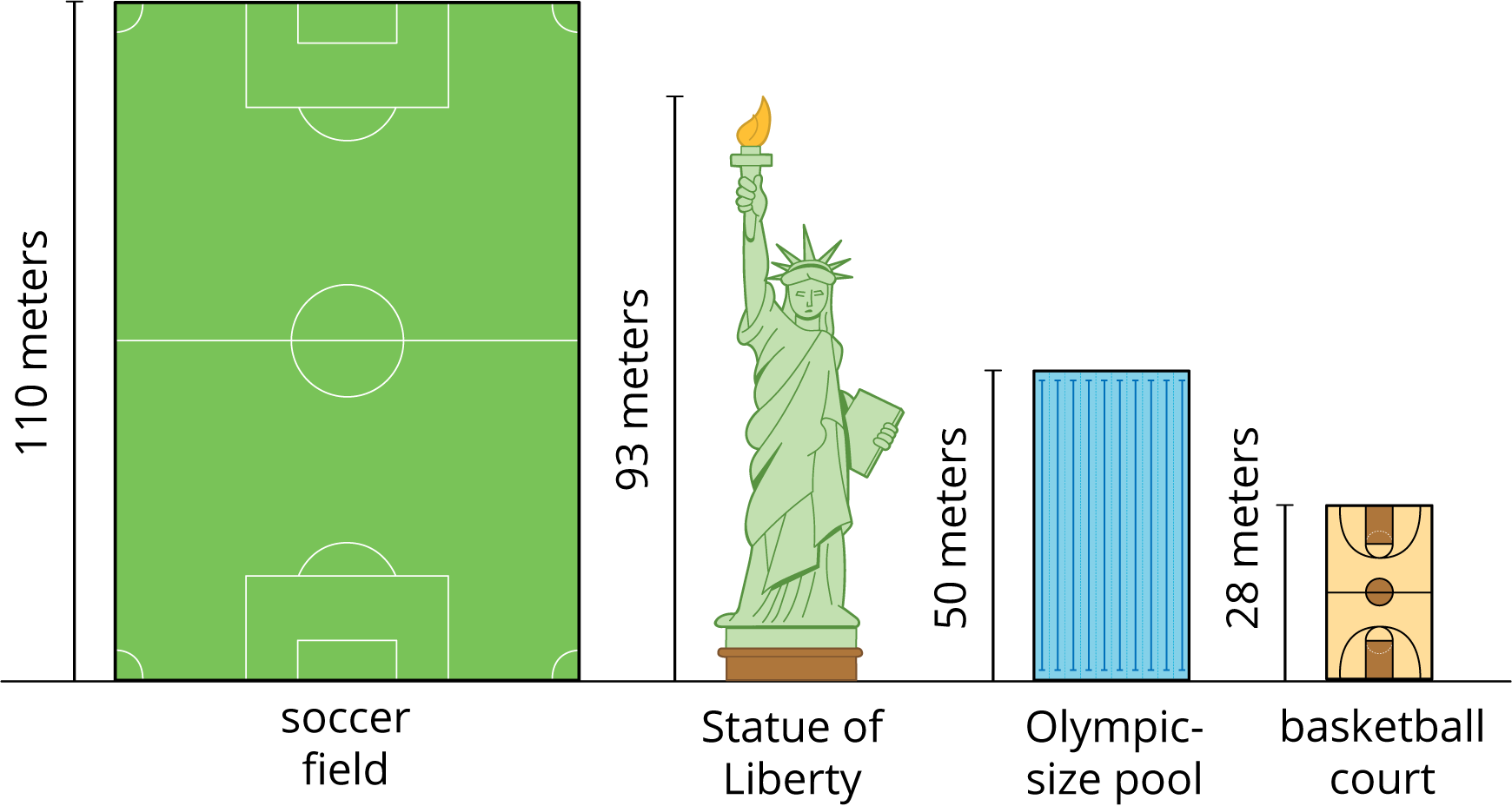
Later, students learn the relationships between grams and kilograms, milliliters and liters, ounces and pounds, and hours, minutes, and seconds. As they solve problems and use multiplication to perform conversion, they develop a sense of the relative size of the units.
Put the animals and their travel distances in order, from the shortest to the longest.
| animal | distance traveled in a day |
|---|---|
| three-toed sloth | 30 meters |
| snail | 2,500 centimeters |
| dromedary | 40 kilometers |
| giant tortoise | 500 meters |
PLC: Lesson 8, Activity 1, How Long is One Kilometer?
Section C: Let’s Put it to Work
Standards Alignments| Addressing | 4.MD.A.1, 4.MD.A.2, 4.MD.A.3, 4.NBT.B, 4.NF.B.4, 4.NF.B.4.c, 4.OA.A.2 |
- Solve multi-step problems involving multiplicative comparison and measurement.
In this section, students use multiplicative comparison and measurement conversion strategies to solve multi-step problems. As they convert customary and metric units of length, mass, and capacity, they continue to develop their understanding of relative sizes of units within the same system.
The problems here involve measurement units introduced in the previous section (pounds, ounces, kilometers, meters, centimeters), some from previous grades (yards, feet, and inches), as well as some new ones (gallons, quarts, and cups). As they make sense of situations, create representations, and write equations to solve problems, students practice reasoning quantitatively and abstractly (MP2).
Students also explore multiplicative relationships in geometric contexts. They analyze the relationship between the side lengths and perimeters of quadrilaterals, performing unit conversion along the way.
Find the perimeter of figure C and the missing side length of figure D.
The perimeter of C is how many times the perimeter of D?

Perimeter = ______________

Perimeter = 12 in
The section ends with an optional lesson in which students apply the understandings from this unit to make sense of measurements related to animals and analyze statements about them.
PLC: Lesson 15, Activity 2, Stone Towers
Estimated Days: 17 - 18
Unit 6: Multiplying and Dividing Multi-digit Numbers
Unit Learning Goals- Students multiply and divide multi-digit whole numbers using partial products and partial quotients strategies, and apply this understanding to solve multi-step problems using the four operations.
In this unit, students extend their knowledge of multiplication and division to find products and quotients of multi-digit numbers.
In grade 3, students learned that they could find the value of a product by decomposing one factor into smaller parts, finding partial products, and then combining them. To support this reasoning, they used base-ten diagrams (decomposing two-digit factors into tens and ones) and area diagrams (decomposing one side length into smaller numbers). Here, students use those understandings to multiply up to four digits by single-digit numbers, and to multiply a pair of two-digit numbers.
Students begin by describing features of geometric and numerical patterns using ideas and language related to multiplication and multiplicative relationships (such as factors, multiples, double, and triple).
Next, students reason about products of multi-digit numbers. They transition from using diagrams to using algorithms to record partial products.
Students learn that they can multiply the factors by place value, one digit at a time, and then organize the partial products vertically. Here are two ways to show partial products for \(3,\!419 \times 8\).


Later, students divide dividends up to four-digit by single-digit divisors. Students see that it helps to decompose a dividend into smaller numbers and find partial quotients, just as it helped to decompose factors and find partial products.
They also recognize that sometimes it is most productive to decompose a dividend by place value. For instance, to find \(465 \div 5\), we can divide each 400, 60, and 5 by 5.
Students encounter various ways to record the division process, including an algorithm that records partial quotients in a vertical arrangement.
At the end of the unit, students apply their expanded knowledge of operations to solve multi-step problems about measurement in various contexts—calendar days, distance, and population.
\(\begin{align} 400\div 5&= 80\\ 60\div 5 &= 12\\ 5 \div 5 &= \phantom{0}1 \\ \overline {\hspace{5mm}465 \div 5} &\overline{\hspace{1mm}= 93 \phantom{000}} \end{align}\)

Section A: Features of Patterns
Standards Alignments| Addressing | 4.OA.C.5 |
- Generate a number or shape pattern that follows a given rule.
- Identify apparent features of a number pattern that were not explicit in the rule itself.
In this section, students observe and describe features of geometric and numerical patterns. Given the rule of a pattern, they predict the values or features of future terms in a pattern sequence. To make predictions, students use their understanding of operations and place value.
The section begins with patterns that are more concrete—such as shapes with features that change quantitatively and thus elicit addition or multiplication. It then moves toward patterns with repeating objects or numbers, which require students to reason more abstractly.
Later, students explore patterns in the features of rectangles—side length, perimeter, and area—that change by a rule. Along the way, students apply their knowledge of factors and multiples.
If the pattern continues, could 50 represent the longer side length or the area of one of the rectangles?
If so, which step? If not, why not?

PLC: Lesson 1, Activity 2, Taller and Taller
Section B: Multi-digit Multiplication
Standards Alignments| Addressing | 4.MD.A.2, 4.NBT.B.4, 4.NBT.B.5, 4.OA.A.3 |
- Multiply a whole number of up to four digits by a one-digit whole number, and 2 two-digit numbers using strategies based on place value and the properties of operations.
In this section, students use their knowledge of multiplication, place value, and area of rectangles to multiply one-digit numbers and numbers up to four digits, and to multiply pairs of two-digit numbers.
A key thread here is the idea of decomposing factors—particularly by place value—as a productive way of finding products. Students explore this idea with concrete and visual representations: arrays, base-ten diagrams, and rectangles with grids. As they decompose larger factors, they see the limits of these representations, motivating more efficient representations and strategies.
In grade 3, students saw that rectangles can help us reason about multiplication—the side lengths of a rectangle can represent the two factors and its area can represent the product. As the factors become larger (for instance, \(3\times 2,\!135\)), it becomes necessary to draw rectangles whose side lengths are not to scale. When rectangles no longer accurately represent area, the term “area diagrams” is not used. Instead, “rectangular diagrams” is used in teacher materials and “diagrams” in student materials.
Students use such diagrams as a visual tool to decompose factors by place value and to organize partial products.
Lin drew a diagram to represent \(3\times2{,}135\).

Complete the diagram.
Use it to find the value of \(3\times2{,}135\).
The benefits of decomposing factors by place value become more apparent as students multiply pairs of two-digit numbers.
They consider, for example, why diagram A may be more helpful than diagram B for finding the value of \(49 \times 57\).


Later, students encounter an algorithm that uses partial products, a different way to record the reasoning they used with diagrams. They learn that the partial products can be listed vertically, instead of inside the boxes of a rectangular diagram.


Students use this algorithm to multiply two-digit numbers, likewise connecting the partial products to the values in a corresponding diagram.
Algorithms that use partial products prepare students to make sense of the standard algorithm for multiplication, which students preview in this unit but will study closely in grade 5.
PLC: Lesson 9, Activity 1, An Algorithm for Noah
Section C: Multi-digit Division
Standards Alignments| Addressing | 4.MD.A.3, 4.NBT.B.6, 4.OA.A.3, 4.OA.B.4 |
- Divide numbers of up to four digits by one-digit divisors to find whole-number quotients and remainders, using strategies based on place value, properties of operations, and the relationship between multiplication and division.
In grade 3, students made sense of division in relation to multiplication and equal-size groups. They reasoned about division problems in context and found whole-number quotients from two-digit dividends and one-digit divisors. Here, students find quotients from larger dividends (up to four digits), investigate new division strategies and ways to represent them, and interpret division situations that involve remainders.
Students begin by solving problems in various situations, including those about equal-size groups, factors and multiples, and area of rectangles. These experiences reinforce students' understanding of the relationship between multiplication and division. They also build students' intuition for the kinds of situations that involve division (including those where a remainder may be involved), before focusing on finding the value of quotients.
Students first reason about division problems in any way that makes sense to them, and later use base-ten representations. They recall that to find the value of \(64 \div 4\), for instance, they could first put 4 tens and 4 ones into 4 groups (1 ten and 1 one in each group), and then decompose the remaining 2 tens into 20 ones and put 5 ones in each group.


Students see that, just as they can distribute blocks of tens and ones into groups incrementally, they can decompose a dividend into parts and find partial quotients.
While there is not a single way to decompose a dividend, doing so by place value is often helpful, as was the case when finding partial products.
Students learn to use a series of equations and a vertical recording method to organize partial quotients.
\(\begin{align} \\ 720\div 9&= 80\\ 18\div 9 &= \phantom{0}2\\ \overline {\hspace{5mm}738 \div 9} &\overline{\hspace{1mm}= 82 \phantom{000}}\end{align} \)

Later in the section, students take a closer look at division problems that do not have whole-number quotients and interpret the remainders in the context of the problem.
PLC: Lesson 15, Activity 1, Elena’s Mural
Section D: Let’s Put It to Work: Problem Solving with Large Numbers
Standards Alignments| Addressing | 4.MD.A.2, 4.MD.A.3, 4.NBT.B.4, 4.NBT.B.5, 4.NBT.B.6, 4.OA.A.2, 4.OA.A.3, 4.OA.C.5 |
- Use the four operations to solve problems that involve multi-digit whole numbers and assess the reasonableness of answers.
In the final section of this unit, students engage with a variety of contextual problems that involve multi-digit numbers and all four operations. The problems can be approached in many ways, presenting students with opportunities to choose their strategies and representations strategically. Many of them also involve multiple steps and justifications, prompting students to practice constructing logical reasoning and critiquing the reasoning of others (MP3).
Jada plans to cut up a sheet of poster paper, rearrange the pieces, and tape them to make a banner that is 8 inches tall and 8 feet long.

Does she have enough paper to make the banner?
Are there more people who only speak English or more people who speak a language other than English?
Show how you know.
| language | number of speakers |
|---|---|
| English only | 1,224,539 |
| Spanish | 127,352 |
| Other Indo-European | 6,750 |
| Asian | 364 |
PLC: Lesson 22, Activity 1, Create a Class Banner
Estimated Days: 24 - 25
Unit 7: Angles and Angle Measurement
Unit Learning Goals- Students learn to draw and identify points, rays, segments, angles, and lines, including parallel and perpendicular lines. Students also learn how to use a protractor to measure angles and draw angles of given measurements, and identify acute, obtuse, right, and straight angles in two-dimensional figures.
In this unit, students deepen and refine students’ understanding of geometric figures and measurement.
In earlier grades, students learned about two-dimensional shapes and their attributes, which they described informally early on but with increasing precision over time. Here, students formalize their intuitive knowledge about geometric features and draw them. They identify and define some building blocks of geometry (points, lines, rays, and line segments), and develop concepts and language to more precisely describe and reason about other geometric figures.
Jada says figure A shows an angle,
but figure B does not. Do you agree?

Students analyze cases where lines intersect and where they don’t, as in the case of parallel lines. They learn that an angle as a figure composed of two rays that share an endpoint.
Later, students compare the size of angles and consider ways to quantify it. They learn that angles can be measured in terms of the amount of turn one ray makes relative to another ray that shares the same vertex.
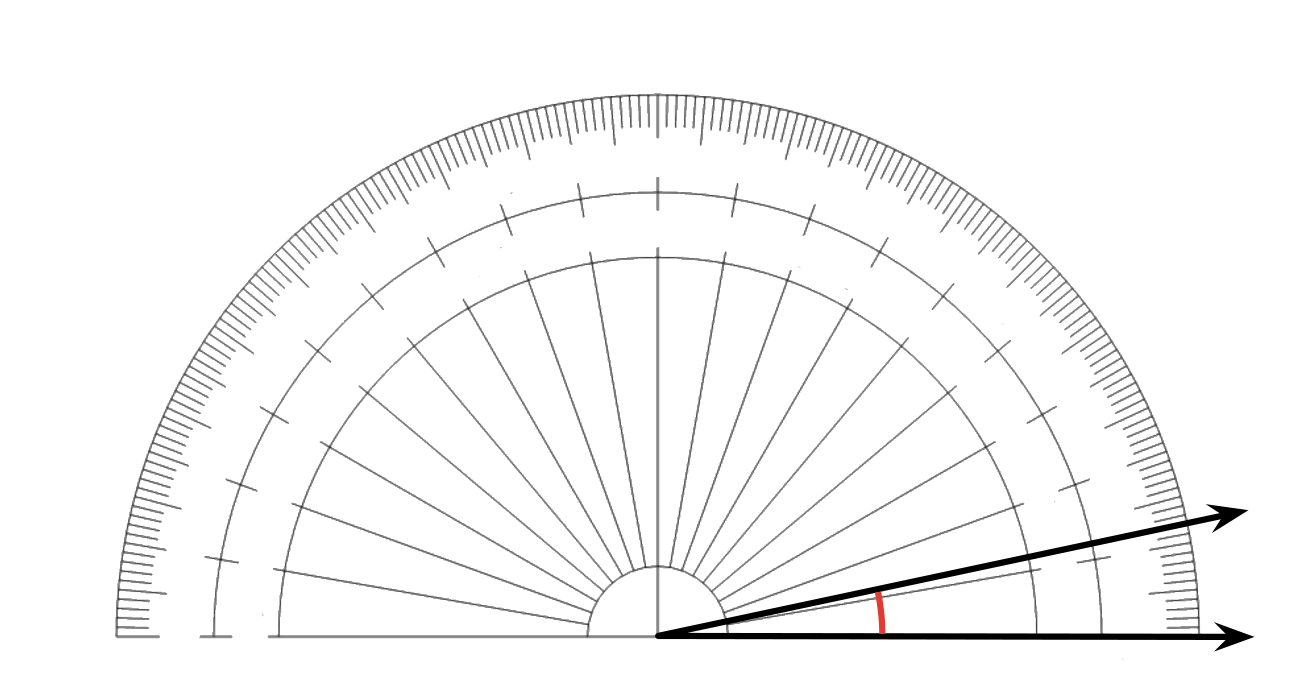
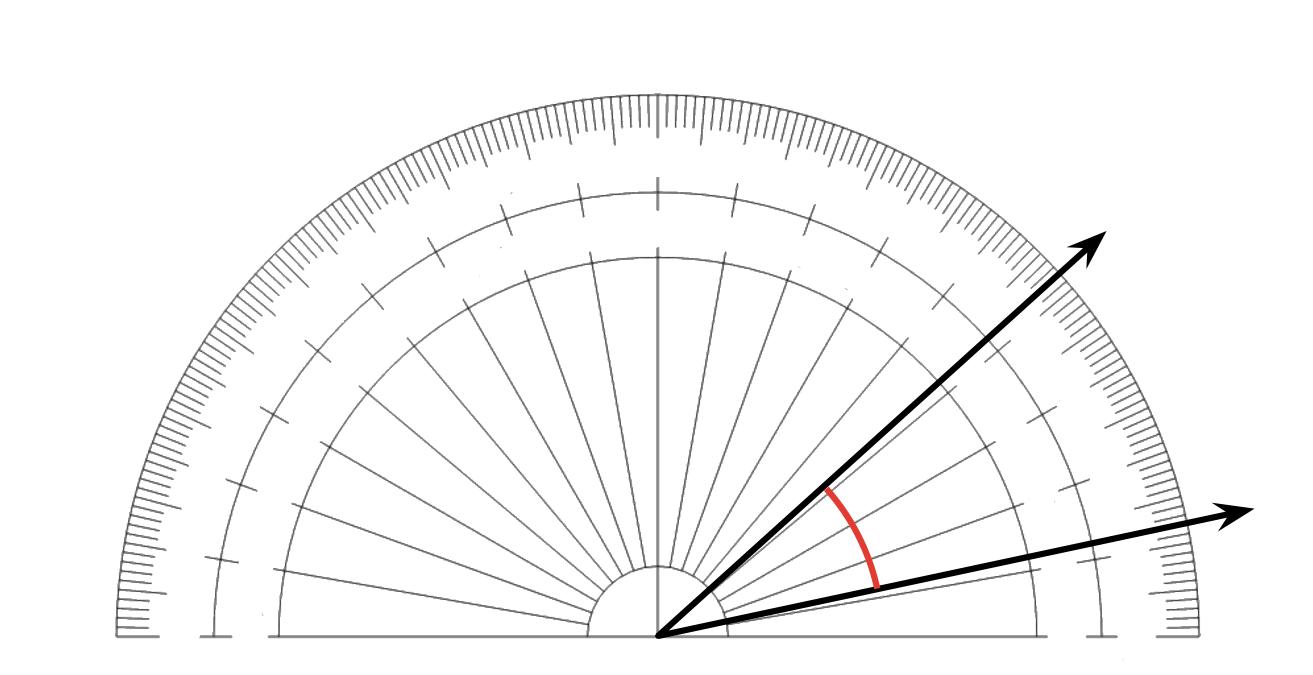
Students come to see that a 1-degree angle is \(\frac{1}{360}\) of a full turn or full circle and can be used to measure angles. They use a protractor to measure angles in whole-number degrees.
Students also learn that angles are additive. When an angle is composed of multiple non-overlapping parts, the measure of the whole is the sum of the angle measures of the parts. These insights enable students to classify angles (as acute, obtuse, right, or straight) and to solve problems about missing angle measurements in concrete and abstract contexts.
How many degrees is each marked angle on the clock? Show your reasoning.


Section A: Points, Lines, Segments, Rays, and Angles
Standards Alignments| Addressing | 4.G.A.1, 4.MD.C.5, 4.NBT.B.4, 4.NBT.B.5 |
- Draw and identify points, lines, rays, segments, and parallel and intersecting lines in geometric figures.
- Recognize that angles are formed wherever two rays share a common endpoint and identify angles in two-dimensional figures.
This section introduces students to some building blocks of geometric figures and the language to describe them. Students start by describing images that contain lines for others to draw and drawing images relying only on others’ descriptions. The experience motivates a need for more precise vocabulary to describe geometric parts. They learn to distinguish points as locations in space, rays as lines that are bounded by one point, and line segments as lines that are bounded by two points.
Students are familiar with lines that cross or intersect. Here, they identify and then draw parallel lines, lines that never intersect.
Students also learn that an angle is a figure that is made up of two rays that share the same endpoint, called the vertex of the angle. They then practice identifying angles, noticing that angles are ubiquitous around us and can have different sizes.
Decide if each figure shows at least one angle.

PLC: Lesson 3, Activity 2, To Cross or Not to Cross
Section B: The Size of Angles
Standards Alignments| Addressing | 4.G.A.1, 4.MD.C.5, 4.MD.C.5.a, 4.MD.C.5.b, 4.MD.C.6, 4.MD.C.7, 4.NBT.B.5, 4.NBT.B.6 |
- Recognize that angles can be measured in degrees, and can be found using addition and subtraction.
- Use a protractor to measure and draw angles, and recognize that perpendicular lines meet or cross at a right angle.
In this section, students learn two main ideas: that angles can be measured, with degrees (\(^\circ\)) as the unit of measurement, and that angles can be composed and decomposed, and are therefore additive. They also learn to use a protractor to measure and draw angles.
Students begin by comparing angles visually and exploring ways to describe their size. They then try to describe angles made by the hour and minute hands of an analog clock, using the numbers and tick marks on the clock or units of time to quantify the size of angles. This experience reinforces the idea of an angle as a figure formed when a ray rotates around a vertex shared with another ray. It also motivates the need for a more precise unit for measuring angles.
Students learn that a ray that makes a full turn around a point makes a \(360^\circ\) angle. Decomposing this angle into halves gives a \(180^\circ\) angle. Half of that angle is a \(90^\circ\) angle or a right angle. Composing three \(90^\circ\) angles gives a \(270^\circ\) angle.
Students then use these benchmark angles to estimate and measure the sizes of other angles. For example, decomposing a right angle into halves gives \(45^\circ\) angles. Composing three copies of a \(45^\circ\) angle makes a \(135^\circ\) angle, and so on.
Students also learn that \(90^\circ\) angles are formed by perpendicular lines.

Later, students make sense of a \(1^\circ\) angle and see that it is \(\frac{1}{360}\) of a full turn. They use a protractor and \(1^\circ\) as a unit for measuring and drawing angles of all sizes.
How many degrees is this angle?
Explain how you know.
An angle contains thirty 1° angles, as shown.
How many degrees is this angle?
Throughout the section, students build their understanding of angles of different sizes using tactile tools such as paper cutouts and patty paper, and by folding, cutting, marking, and assembling pieces of paper.
Section C: Angle Analysis
Standards Alignments| Addressing | 4.G.A.1, 4.G.A.2, 4.MD.C.6, 4.MD.C.7 |
- Draw and identify acute, obtuse, right, and straight angles in two-dimensional figures.
- Write equations to represent angle relationships and reason about and find unknown measurements.
In this section, students continue to draw and analyze angles and reason about their measurements.
They first classify angles by their size and identify acute, obtuse, and straight angles. Then, they further develop the idea that angle is additive by composing and decomposing angles, using tactile tools and drawings, and writing expressions or equations to support their reasoning.
Students solve problems about angles in different contexts, both concrete and abstract. They use their understanding of right angle and straight angle to reason about unknown angle measurements.
Find the measurement of each shaded angle. Show how you know.

PLC: Lesson 14, Activity 2, Tick Tock
Estimated Days: 15 - 16
Unit 8: Properties of Two-dimensional Shapes
Unit Learning Goals- Students classify triangles and quadrilaterals based on the properties of their side lengths and angles, and learn about lines of symmetry in two-dimensional figures. They use their understanding of these attributes to solve problems, including problems involving perimeter and area.
In this unit, students deepen their understanding of the attributes and measurement of two-dimensional shapes.
Prior to this unit, students learned about some building blocks of geometry—points, lines, rays, segments, and angles. They identified parallel and intersecting lines, measured angles, and classified angles based on their measurement. Here, they apply those insights to describe and reason about characteristics of shapes.
In the first half of the unit, students analyze and categorize two-dimensional shapes—triangles and quadrilaterals—by their attributes. They classify two-dimensional shapes based on the presence or absence of parallel or perpendicular lines, or the presence or absence of angles of a specified size. Students also learn about symmetry. They identify line-symmetric figures and draw lines of symmetry.
Quadrilaterals N, U, and Z are parallelograms.

Quadrilaterals AA, EE, and JJ are rhombuses.

Write 4–5 statements about the sides and angles of the quadrilaterals in each set.
Each statement must be true for all the shapes in the set.
The second half of the unit gives students opportunities to apply their understanding of geometric attributes to solve problems about measurements (side lengths, perimeters, and angles).
Included in this unit are three optional lessons that offer opportunities for students to strengthen and extend their understanding of symmetry and other attributes of two-dimensional shapes.
Section A: Side Lengths, Angles, and Lines of Symmetry
Standards Alignments| Addressing | 4.G.A.1, 4.G.A.2, 4.G.A.3, 4.MD.C, 4.NBT.B.5, 4.NF.B.3.c, 4.NF.B.4 |
- Classify triangles (including right triangles), parallelograms, rectangles, rhombuses, and squares based on the properties of their side lengths and angles.
- Identify and draw lines of symmetry in two-dimensional figures.
This section prompts students to consider different ways of looking at two-dimensional shapes: by the number of sides, length of sides, size of angles, presence of parallel or perpendicular lines, and symmetry. Students examine these attributes in shapes, classify the shapes by the attributes, and explain their classifications. For example, they identify quadrilaterals as parallelograms if they have two pairs of parallel sides, as squares if they have four equal sides and four right angles, and so on.
In studying symmetry, students characterize shapes based on whether they can be folded into two equal halves that match up exactly, draw lines of symmetry, and complete drawings of figures that are halved by a line of symmetry.
Lin folds pieces of paper in different shapes.
She sorts them into two categories based on the folding lines.
Study the shapes in each category. What do you think a ‘line of symmetry’ means?
The section includes one optional lesson in which students apply their understanding of two-dimensional shapes to complete or create drawings of figures with specified attributes.
PLC: Lesson 3, Activity 1, Quadrilateral Hunt
Section B: Reason about Attributes to Solve Problems
Standards Alignments| Addressing | 4.G.A.1, 4.G.A.2, 4.G.A.3, 4.MD.A, 4.MD.A.3, 4.MD.C.7, 4.NF.B.3.c, 4.NF.B.4, 4.NF.B.4.b |
- Solve problems involving unknown side lengths, perimeter, area, and angle measurements using the known attributes and properties of two-dimensional shapes.
In this section, students apply their knowledge of geometric attributes to reason about measurements in various two-dimensional shapes. They find the perimeter of shapes where the side lengths are all given. Then, they move on to cases where the side lengths are not explicitly given but can be deduced based on information about the shapes.
Later, students are given the perimeter and some information about a shape and find any unknown side lengths. The activities also enable students to practice performing operations on whole numbers and fractions.
Here are four figures, each with a perimeter of 64 inches.
Figures P, Q, and R each have 1 line of symmetry. Figure Q has 4 lines of symmetry.

Draw the lines of symmetry of each figure and find the unknown side length.
In the last two lessons, students use what they have learned about symmetry to solve problems related to perimeter and unknown angle measurements in two-dimensional shapes. This work deepens students’ understanding of the concepts from this unit and offers opportunities to practice reasoning about angle measurement, but it is not required by grade 4 standards. These lessons are therefore optional.
PLC: Lesson 8, Activity 2, Lin’s Design
Estimated Days: 7 - 10
Unit 9: Putting It All Together
Unit Learning Goals- Students consolidate and solidify their understanding of various concepts and skills related to major work of the grade. They also continue to work toward fluency goals of the grade.
In this unit, students revisit major work and fluency goals of the grade, applying their learning from the year.
In Section A, students reinforce what they learn about comparing fractions, adding and subtracting fractions, and multiplying fractions and whole numbers. In Section B, they strengthen their ability to add and subtract multi-digit numbers fluently using the standard algorithm. They also multiply and divide numbers by reasoning about place value and practice doing so strategically.
Here are the times of the runners for two teams.
Which team won the relay race?
| runner | Diego’s team, time (seconds) | Jada’s team, time (seconds) |
|---|---|---|
| 1 | \(10\frac{25}{100}\) | \(11\frac{9}{10}\) |
| 2 | \(11\frac{40}{100}\) | \(9\frac{8}{10}\) |
| 3 | \(9\frac{7}{10}\) | \(9\frac{84}{100}\) |
| 4 | \(10\frac{5}{100}\) | \(10\frac{60}{100}\) |

In Section C, students practice making sense of situations and solving problems that involve reasoning with multiplication and division, including multiplicative comparison and interpreting remainders. In the final section, students review major work of the grade as they create activities in the format of the warm-ups routines they have encountered throughout the year (Estimation Exploration, Number Talk, and Which One Doesn’t Belong?).
The sections in this unit are standalone sections, not required to be completed in order. Within a section, lessons can also be completed selectively and without competing prior lessons. The goal is to offer ample opportunities for students to integrate the knowledge they have gained and to practice skills related to the expected fluencies of the grade.
Section A: Reason with Fractions
Standards Alignments| Addressing | 4.NF.A.1, 4.NF.A.2, 4.NF.B.3, 4.NF.B.3.a, 4.NF.B.3.b, 4.NF.B.3.c, 4.NF.B.3.d, 4.NF.B.4, 4.NF.C.5, 4.NF.C.6, 4.NF.C.7 |
- Solve problems involving fraction equivalence and operating with fractions.
In this section, students solve problems that require multiplying fractions by whole numbers and adding and subtracting fractions with the same denominator.
They apply the reasoning strategies developed in the course and their understanding of fractions and equivalence to compare fractions, add and subtract whole numbers and fractions (including mixed numbers), and find sums and differences of tenths and hundredths.
The lessons also prompt students to reason about fractional quantities in a variety of contexts that invite them to share their own cultural experiences and learn about the experiences of others.
Jada and Lin are making head wraps from African wax print fabric.

Jada stitches together 5 pieces of fabric that each have a length of \(\frac{2}{6}\) yard.
Lin stitched together 3 pieces of fabric that are each \(\frac{2}{3}\) yard long.
Who used more fabric?
PLC: Lesson 1, Activity 1, Let’s Make Head Wraps!
Section B: Whole-number Operations
Standards Alignments| Addressing | 4.NBT.B, 4.NBT.B.4, 4.NBT.B.5, 4.NBT.B.6 |
- Add, subtract, multiply, and divide multi-digit numbers using place value understanding.
In this section, students deepen their understanding of place value and build their fluency in performing operations on multi-digit numbers.
Students begin by practicing the standard algorithm for addition and subtraction. They also attend to potential errors in using the algorithm, particularly when it is necessary to decompose or compose a base-ten unit multiple times, as in the case when subtracting from a number with zeros. Students consider different strategies for approaching multi-digit subtraction, including by leveraging the relationship between addition and subtraction.
To find the value of \(20,\!000 - 472\), Priya and Han set up their calculations differently.
Use both methods to find the difference of 20,000 and 472.


Next, they practice multiplying and dividing multi-digit numbers using algorithms that involve partial products and partial quotients. In both cases, students analyze and make connections across different methods of recording the process of multiplication and division. The work here prepares students to study the standard algorithm for multiplication and for division more closely in grade 5.
Here are two ways to find \(34 \times 21\).
In method A, where do the 4, 30, 80, and 600 come from?
In method B, which two numbers are multiplied to get 34? 680?


PLC: Lesson 4, Activity 1, Lots of Zeros
Section C: Solve Problems with Multiplication and Division
Standards Alignments| Addressing | 4.NBT.B, 4.NBT.B.4, 4.NBT.B.5, 4.NBT.B.6, 4.OA.A.2, 4.OA.A.3 |
- Solve problems involving measurement comparison.
In this section, students practice solving real-world problems using multiplication and division. Throughout the section, students reason with mathematics in different ways. They look for ways to compare quantities with addition or multiplication. They make estimates to simplify a problem or to assess the reasonableness of a statement or value before and after performing calculations. They also continue to reason with diagrams and equations, connecting these representations and the solution to a problem back to the context of the problem.
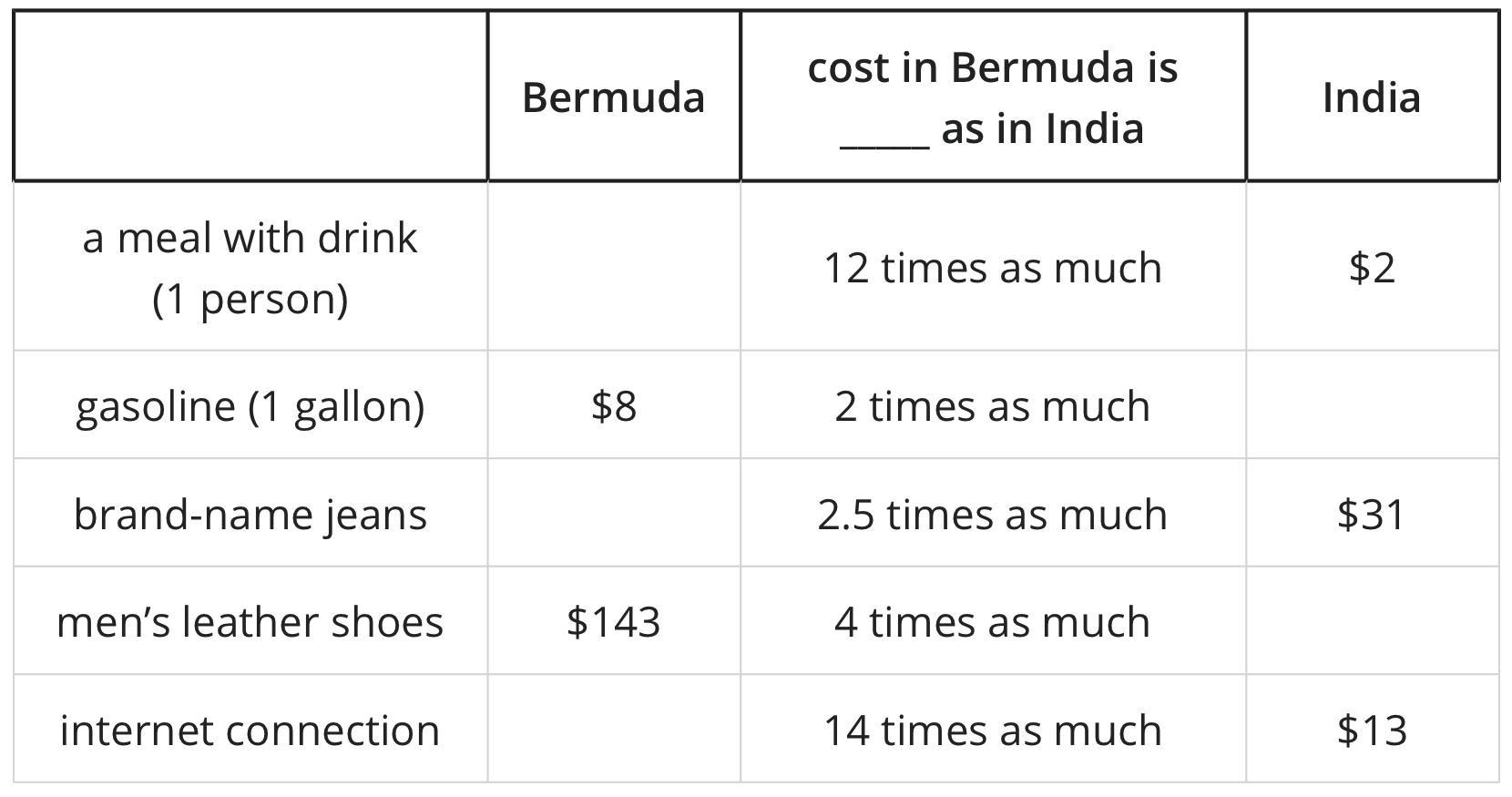
Students encounter problems that involve division and multiplication with large numbers, but are not expected to divide by multi-digit divisors. All problems can be reasoned and estimated by multiplication, by rounding, and by relating the quantities to nearby multiples of 10 or 100. In one lesson, students have the opportunity to formulate their own problems given a context and some parameters about the situation.
PLC: Lesson 7, Activity 1, The Most and Least Expensive
Section D: Creation and Design
Standards Alignments| Addressing | 4.G.A.1, 4.NBT.A, 4.NBT.A.1, 4.NBT.B, 4.NBT.B.5, 4.NF.B, 4.NF.B.4, 4.OA, 4.OA.A, 4.OA.A.3, 4.OA.B.4, 4.OA.C, 4.OA.C.5 |
- Review the major work of the grade by creating and designing instructional routines.
Throughout the course, students have engaged in warm-up routines such as How Many Do You See, Exploration Estimation, Which One Doesn’t Belong, True or False, and Number Talk. This section enables them to apply the mathematics they have learned to design warm-ups that incorporate some of these routines
Each lesson is devoted to a particular routine. Students begin by completing at least two partially created tasks, each with more missing parts to complete than the previous one. They practice anticipating responses that others might give to the prompts they pose.

a. Find at least one reason that all items belong in the set.
b. Find at least one reason that each item doesn’t belong.
c. Add an item to complete each set. Make sure there is at least one reason it belongs and one reason it doesn’t belong.
Along the way, students gain the skills and insights needed to create an activity from scratch or with minimal scaffolding. In each lesson, students have the option to facilitate their activity with another group in the class.
PLC: Lesson 11, Activity 2, Add Two That Don’t Belong
Estimated Days: 12

