Lesson 19
Flexible with Fractions (optional)
Warm-up: Notice and Wonder: Sticky Notes (10 minutes)
Narrative
This warm-up prompts students to make sense of a problem before solving it, by familiarizing themselves with a context and the mathematics that might be involved. Students observe images that show three ways of making a T shape using sticky notes, a context they will see in the first activity.
This prompt gives students opportunities to look for structure (MP7)—specifically, the number and orientation of sticky notes of which each T shape is composed—and make use of it to solve problems later.
Launch
- Groups of 2
- Display the image.
- “What do you notice? What do you wonder?”
- 1 minute: quiet think time
Activity
- “Discuss your thinking with your partner.”
- 1 minute: partner discussion
- Share and record responses.
Student Facing
What do you notice? What do you wonder?



Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
- “All three Ts are made of the same number of sticky notes. Do the Ts have the same width and height?” (No)
- “Why might that be?” (The sticky notes have a longer side and a shorter side, and are not all oriented the same way.)
Activity 1: Sticky-note Designs (25 minutes)
Narrative
This optional activity prompts students to analyze a design problem that involves fractional measurements. Students determine which of the three designs they saw in the warm-up would fit on a folder that is 9 inches wide and 12 inches tall. To do so, they find the heights and widths of each design using addition, subtraction, multiplication, or a combination of operations.
Supports accessibility for: Conceptual Processing, Organization, Memory
Required Materials
Materials to Gather
Required Preparation
- Each group needs 12 small sticky notes measuring 1\(\frac{7}{8}\) by 1\(\frac{3}{8}\) inches.
Launch
- Groups of 2–4
- Read the task together as a class.
- “What do you think the problem is asking? What questions do you need answered before working on it?”
- 1 minute: group discussion
- Share responses. Clarify any confusion before students begin the task.
Activity
- “Work independently on the task for about 8–10 minutes. Then, discuss your thinking with your group.”
- 10 minutes: independent work time
- 5 minutes: group discussion
Student Facing

Tyler is using small sticky notes to make a T shape to decorate a folder.
The longer side of the sticky note is \(\frac{15}{8}\) inches. The shorter side is \(\frac{11}{8}\) inches. The folder is 9 inches wide and 12 inches tall.
Here are three ways he could arrange the sticky notes.



Is the folder tall enough and wide enough for his designs? If so, which design(s) would fit? Show your reasoning.
Student Response
For access, consult one of our IM Certified Partners.
Advancing Student Thinking
Activity Synthesis
- Invite a group to share their response and reasoning on each design. Display their reasoning or record it for all to see.
- Ask others if they agree and if approached it the same way.
- Explain to students that they will now verify their responses. Assign one design for each group to verify.
- Give 12 small sticky notes (measuring \(1\frac{7}{8}\) by \(1\frac{3}{8}\)) to each group. Ask students to use the sticky notes to create the design.
- Next, give each group an inch ruler and ask them to measure if their design is less than 9 inches wide and less than 12 inches tall.
Activity 2: Hiking Trails (20 minutes)
Narrative
This optional activity offers students to interpret and solve problems involving fractional measurements and operations of fractions in the context of distances on a map. First, students examine the measurements on the map and use them to answer questions. Next, they interpret given expressions and consider what the expressions might represent in the situation. Finally, they write a new problem based on the given quantities and information. The work here prompts students to reason quantitatively and abstractly (MP2).
This activity uses MLR6 Three Reads. Advances: reading, listening, representing
Launch
- Groups of 2
MLR6 Three Reads
- Display only the problem stem, without revealing the question(s).
- “We are going to read this problem 3 times.”
- 1st Read: “Jada and Noah’s class are hiking at a park. Here is a map of the trails. The length of each trail is shown.”
- “What is this situation about?”
- 1 minute: partner discussion
- Listen for and clarify any questions about the context.
- 2nd Read: “Jada and Noah’s class are hiking at a park. Here is a map of the trails. The length of each trail is shown.” (Display the trail map.)
- “Name the quantities. What can we count or measure in this situation?”
- 30 seconds: quiet think time
- 2 minutes: partner discussion
- Share and record all quantities.
- Reveal the question(s).
- 3rd Read: Read the entire problem, including question(s) aloud.
- “What are some strategies we can use to solve this problem?”
- 30 seconds: quiet think time
- 1–2 minutes: partner discussion
Activity
- “Work independently on the task for 10 minutes. Then, discuss your responses and complete the last problem with your partner.”
- 10 minutes: independent work time
- 3–4 minutes: group work time
Student Facing
Jada and Noah’s class are hiking at a park. Here is a map of the trails. The length of each trail is shown.
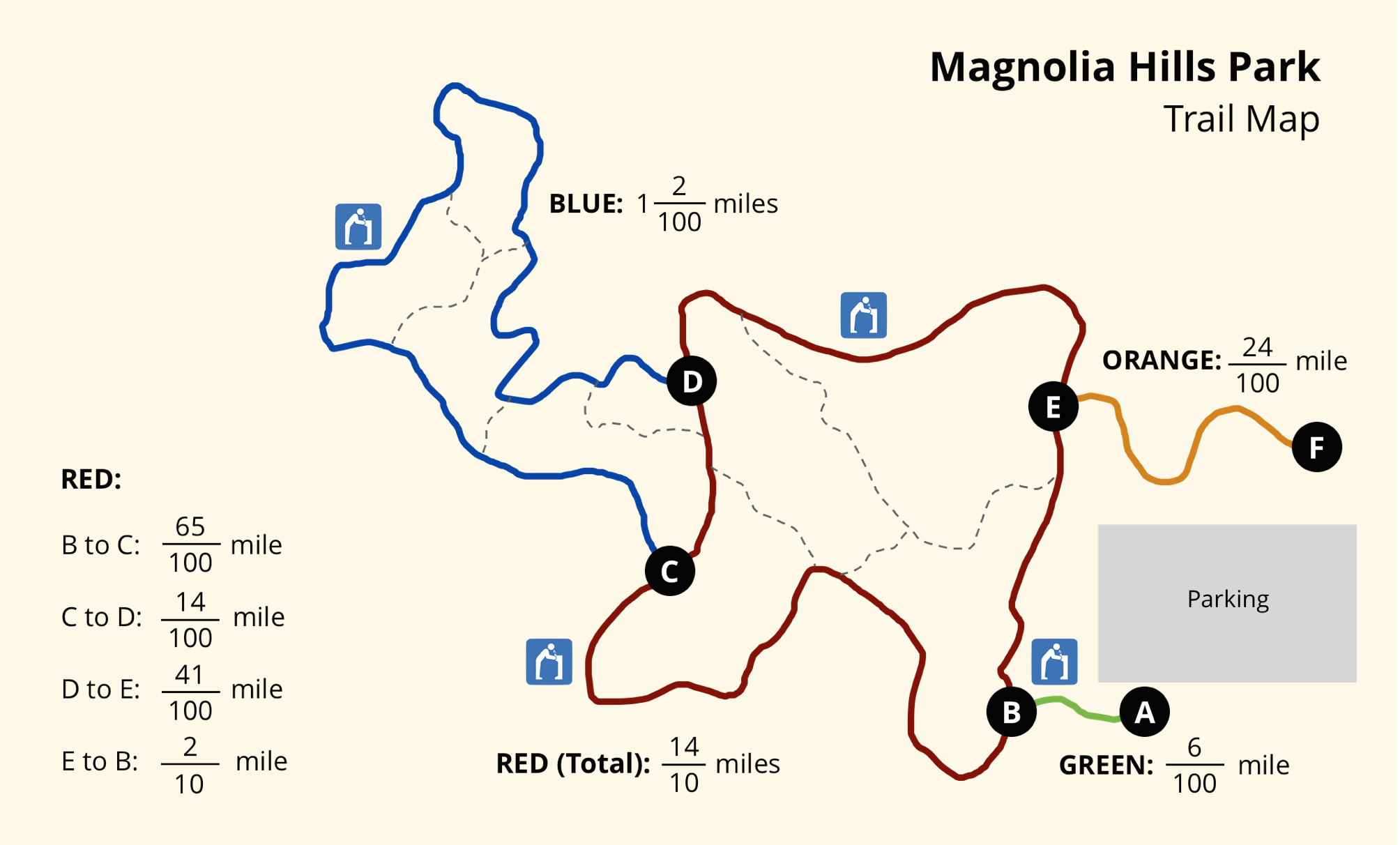
-
Jada and Noah hike the orange trail from point F to point E, make one full loop on the red trail back to point E, and then hike from E back to F.
How many miles do they hike? Show your reasoning.
-
Here are two expressions that represent some hiking situations and can help to answer two questions. What question might each expression help to answer? Write the question and the answer.
- \(\frac{6}{100} + \frac{65}{100} + 1\frac{2}{100} + \frac{41}{100} + \frac{24}{100}\)
- \(\left(2 \times \frac{14}{10}\right) + \left(2 \times \frac{6}{100}\right)\)
- Use the distances on the map to write a new question and find its answer. Then, trade questions with a partner and answer one another's question.
Student Response
For access, consult one of our IM Certified Partners.
Activity Synthesis
-
Invite 2–3 students to share their responses to the last two problems.
Activity 3: Find a Match (25 minutes)
Narrative
In this optional activity, students hone the skills they have learned in this unit: multiplying a fraction by a whole number, adding and subtracting fractions with the same denominator (including mixed numbers), and adding tenths and hundredths. Students are each given a fractional expression. They evaluate the expression, find a classmate whose expression is different but has the same value (verifying that this is indeed the case), and write a new expression that also has the same value. (See Student Responses for the matched expressions.)
In addition to evaluating expressions, students who have cards J, K, and L will also need to think about fractions that are equivalent to the value of their expression in order to find their matches. For instance, a student may reason that the value of card K is \(\frac{8}{10}\) or \(\frac{80}{100}\), but the match—card 2—shows \(\frac{4}{5}\). Consider using these expressions to differentiate for students who could use an extra challenge.
Required Materials
Required Preparation
- Create one set of Match Cards for each group of 24 students.
Launch
- Give one card from the blackline master to each student.
- Tell students that they are to find the value of the expression, and then find a classmate in the class whose expression has the same value.
- “If your expression is labeled with a letter, your match is someone whose expression is labeled with a number. And vice versa.”
- “Once you’ve found your match, complete the rest of the task as directed in the task statement.”
Activity
- 7–8 minutes: independent work time on the first problem and then matching time
- 7–8 minutes: partner work time
- Give each group tools for creating a visual display. Ask them to show that their two expressions are a match, and that their new expressions also have the same value.
Student Facing
Your teacher will give you one card with an expression on it.
- Find the value of the expression.
- Find a classmate whose card also has the same value. Prove to each other that you’re a match.
- Work with your partner to find at least two features that your expressions share (other than the fact that they have the same value.)
- Write one more expression that has the same value but uses a different operation.
Student Response
For access, consult one of our IM Certified Partners.
Advancing Student Thinking
Activity Synthesis
- Ask students to display their work around the room.
- “Take a few minutes to walk around and look at the work of at least 3 other groups.”
- “As you study others’ work, pay attention to how the work is like and unlike yours.”
- 6–7 minutes: gallery walk
- “What is the same about the calculations that you saw? What is different?”
- 1 minute: quiet think time
- Discuss responses.
Lesson Synthesis
Lesson Synthesis
“In the past few lessons, we solved a variety of problems that involve fractions and operations of fractions. We saw problems about situations and those that are not about situations.”
“What were some helpful ways to get started when solving problems with fractions?” (Make sense of the problem and what it is asking. Read any word descriptions carefully and more than one time. Make sense of the quantities.)
“What were some helpful ways to prevent making common errors?” (Check the numbers, including numerators and denominators, carefully. Think about what the numbers mean in the situation.)
“How did you know if your answers make sense?” (Check to see if the result makes sense in the situation. Discuss with a partner. Work backwards from the solution toward the problem.)
Cool-down: Han’s Design (5 minutes)
Cool-Down
For access, consult one of our IM Certified Partners.